ПРОГРАММИРОВАННОЕ ПОСОБИЕ
По математике
по теме: «Методы интегрирования»
Г. Иркутск
Г
Рассмотрено на заседании
Цикловой комиссии от 5 мая 2016 г.
Протокол №9
Председатель ЦК социально-гуманитарных дисциплин Т.А. Головина
Автор: Т.Н. Лапаева
Программированное пособие предназначено для самостоятельного изучения темы «Методы интегрирования» по дисциплине «Математика» студентами 2-го курса. Каждая тема содержит кадр информации, операционный кадр и кадр обратной связи. Так же в конце пособия есть указания к ответам.
УКАЗАНИЯ ДЛЯ СТУДЕНТА
Материал разбит на короткие информации. К каждой информации даются решенные примеры и задания для самостоятельной работы студента. Решив пример, студент должен обязательно сделать проверку решения дифференцированием. После этого он может проверить ответ, открыв брошюру с указаниями к ответам.
Если задание выполнено верно, студент может переходить к следующему заданию. При неправильном ответе он читает разъяснения и указания о дальнейших действиях.
После каждого занятия студент выполняет контрольную работу, которая служит для самоконтроля. Проверка работ может быть выполнена самими студентами. После прохождения всего материала данного пособия дается контрольная работа на оценку.
Занятия программированного обучения требуют от студентов внимания и точного соблюдения всех указаний преподавателя и данного пособия.
В пособии приняты следующие условные обозначения:
1. Информация обозначается буквой «И» с римской цифрой в индексе, что означает номер информации. Например:  – информация первая.
– информация первая.
Считаем известными следующие свойства неопределенного интеграла:
 dx (1) dx (1)
|

|
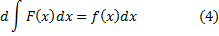
|

|
ТЕМА №1
Непосредственное интегрирование

|

|
Формула справедлива для любого n, кроме n=-1, т.к. в этом случае знаменатель обращается в ноль.
Пример 1: 
1. Применяя свойство (2) (см. выше), разбиваем интеграл суммы на сумму интегралов: 
2. Применяя свойство (1) (см. выше), выносим постоянный множители за знак интеграла: 7 
В первых трех интегралах применяем  , в четвертом интеграле используем свойство (3), получаем: 7
, в четвертом интеграле используем свойство (3), получаем: 7 
Окончательно:  =7
=7 
Пример 2:  .
.
1. Разделим почленно числитель на знаменатель: 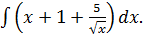
2. а) Воспользуемся свойством (2) – разобьем интеграл на сумму интегралов;
б) Заменим корень дробным показателем;
в) Согласно свойству (1) вынесем 5 за знак интеграла: 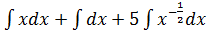
3. Согласно  и свойству (3) имеем:
и свойству (3) имеем: 

Окончательно:  =
= 
Пример 3:  dx
dx
1. Заменим корни дробными показателями: 
2. Произведем действия под интегралом: 
3. По  получаем:
получаем: 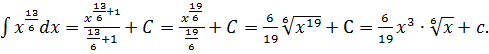
Теперь необходимо выполнить задание в таблице и определить правильный ответ.
Задание №1.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) 
|
| 2. | 
| 1)  ; 2) ; 2) 
|
| 3. | 
| 1) 
|
| 4. | 
| 1) 
|
| 5. | 
| 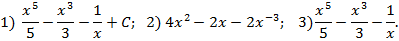
|
 +C +C
|

|
Пример 1: 
1. Делим почленно числитель на знаменатель и разбиваем на сумму интегралов: 
2. На основании  и
и  получаем:
получаем: 
3. Окончательно: 
Пример 2: 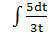
1. По свойству 1 выносим  за знак интеграла
за знак интеграла 
2. Применяя  получим:
получим: 
Задание №2.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) 

|
| 2. | 
| 1) 
|

|

|
Пример 1. 
1. Применяя свойства (1) и (2) (см. стр. 1), получим: 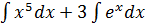 .
.
2. По  и
и  имеем:
имеем: 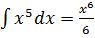 +C; 3
+C; 3 
3. Окончательно:  .
.
Задание №3.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) 
 +C. +C.
|

|

|
Пример 1.  dx=
dx= 
Пример 2. 
Задание №4.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) 
 . .
|
| 2. | 
|
1) -  2) 2
2) 2 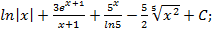 3) 2
3) 2 
|

|

|
Пример 1. 
Пример 2. 
Заменим под знаком интеграла sin2x на 2sinxcosx, тогда числитель дроби примет следующий вид:
 .
.
Задание №5.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) –cosx+C; 2) x+cosx+C; 3) x-cosx+C; 4) 1-cosx+C |
| 2. | 
| 1)-5cosx+5x+C; 2) 5cosx+5x+C; 3)  4) -5cosx+5+C
4) -5cosx+5+C
|

|
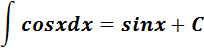
|
Пример 1. 
Применим формулу:  при
при  .
.
 +C.
+C.
Пример 2.  .
.
Задание №6.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) -2sinx+C; 2) 2sinx+C; 3) 
|
| 2. | 
| 1)  2)
2)  . .
|

|

|
Пример 1.  .
.
Решение:
1) Делим почленно числитель на знаменатель и разбиваем интеграл на сумму интегралов: 
2) По  , свойству (3) и
, свойству (3) и  получим:
получим:
 = sinx+3x-5tgx+C
= sinx+3x-5tgx+C
Пример 2. 
Воспользуемся формулами:  .
.

Пример 3. 
Воспользуемся формулой:  ,
,

Задание №7.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) 
|

|

|
Пример 1.  .
.
Воспользуемся формулой: 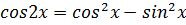

Пример 2.  .
.
Воспользуемся формулами: 


Пример 3.  .
.
Воспользуемся формулой: 1= 

Задание №8.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) cosx+2tgx+C; 2) –cosx+2tgx+C |
| 2. | 
| Указание: Раскрыть скобки, представить ка сумму интегралов. 1) –ctgx+3tgx+cosx+C; 2) сtgx+3tgx+cosx+C. |

|

|
Пример 1. 
Вынесем константу  за знак интеграла:
за знак интеграла: 

Пример 2. 
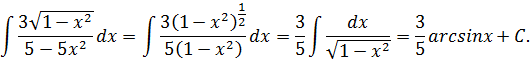
Пример 3.

Задание №9.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 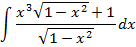
| 1)  3)
3) 
|

|

|
Пример 1.  =
= 
Пример 2.  =
= 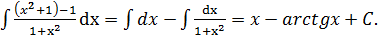
Задание №10.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. |  dx dx
| 1)-  +C;
3) tgx+3arctgx+C; 4) tgx+3arctgx. +C;
3) tgx+3arctgx+C; 4) tgx+3arctgx.
|
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1.  dx; 3.
dx; 3. 
5.  6.
6. 
7.  .
.
ТЕМА №2






