Система n линейных уравнений с n неизвестными x 1, x 2,..., x n
(1)
называется системой линейных уравнений n -го порядка; a ij – коэффициенты, b i– свободные члены системы.
Численные методы решения систем линейных уравнений делятся на прямые и итерационные.
Прямые методы позволяют получить в принципе точное решение за конечное количество арифметических операций, однако при увеличении порядка n системы возрастает погрешность вычисления неизвестных x 1, x 2,..., x n.
Итерационные методы позволяют получать решение с заданной точностью на основе алгоритмов, использующих последовательное приближение (итерацию), однако эффективность итерационных алгоритмов существенно зависит от удачного выбора начального приближения и быстроты сходимости итерационного процесса.
Один из прямых методов, который достаточно просто реализуется средствами Microsoft Excel, использует вычисление обратной матрицы.
Если представить систему линейных уравнений (1) в матричном виде
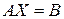, (2)
где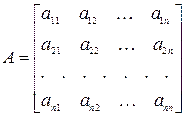 
– матрица коэффициентов,
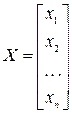– вектор-столбец неизвестных,
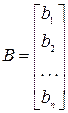– вектор-столбец свободных членов, то решение системы (2) находится следующим образом
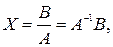(3)
где 
– матрица, обратная к матрице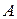 
.
Пример
Найти решение системы линейных уравнений
(4)
двумя методами: прямым, с использованием обратной матрицы, и итерационным. Сравнить полученные решения.
Методические рекомендации
1. Запустите приложение Microsoft Excel 2010: Пуск → Все программы → Microsoft Office → Microsoft Excel 2010. В окне Excel откроется новая рабочая книга с тремя листами.
2. Сохраните рабочую книгу в своей рабочей папке на диске или на личном внешнем носителе: вкладка Файл – команда Сохранить как. Дайте имя файлу Л.р.№4-пример.
3. Замените имя текущего рабочего листа. Для этого дважды щелкните левой кнопкой мыши по ярлычку рабочего листа с надписью Лист1 и наберите имя листа Прямой метод.
4. Для решения системы линейных уравнений (4) с помощью обратной матрицы сформируйте массивы коэффициентов, как показано на рисунке 2.1.
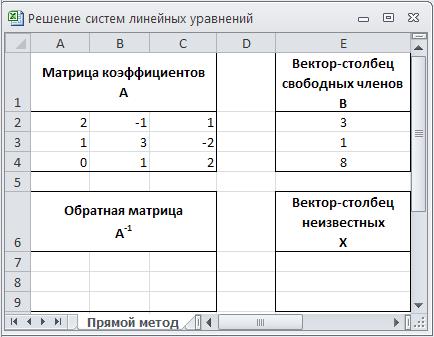
Рис. 2.1. Массивы коэффициентов
5. Для формирования обратной матрицы занесите в ячейку A7 функцию МОБР, аргументом которой является диапазон ячеек А2:С4 с матрицей коэффициентов системы линейных уравнений (4), как показано на рисунке 2.2.
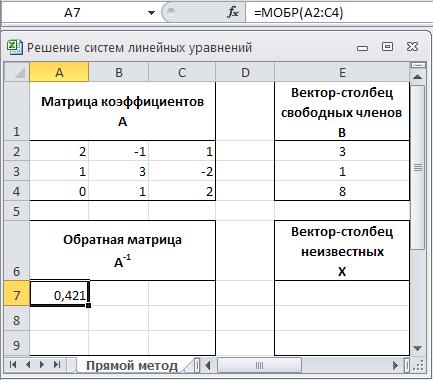
Рис. 2.2. Использование функции МОБР для формирования обратной матрицы
6. Выделите диапазон ячеек A7:C9 в котором будут находится коэффициенты обратной матрицы, нажмите клавишу F2, а затем комбинацию клавиш Ctrl+Shift+Enter. Полученная обратная матрица должна выглядеть так, как показано на рисунке 2.3.
7. Сформируйте выражение для вычисления первого элемента вектора-столбца неизвестных X по формуле (3). Для этого в ячейке E7 запишите выражение для умножения элементов первой строки обратной матрицы A-1 на вектор-столбец свободных членов B =A7*E$2+B7*E$3+C7*E$4, как показано на рисунке 2.4.
Здесь используется абсолютная адресация по строкам для того, чтобы при копировании формулы в ячейки диапазона E8:E9 номера строк, в которых расположены значения элементов вектора-столбца свободных членов B, не изменялись.
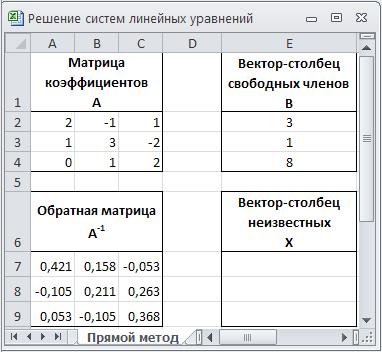
Рис. 2.3. Формирование обратной матрицы
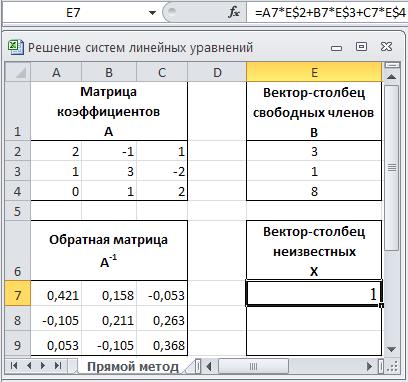
Рис. 2.4. Формирование первого элемента вектора-столбца неизвестных X
8. Пользуясь маркером заполнения, скопируйте формулу из ячейки E7 в ячейки диапазона E8:E9. Полученное таким образом решение системы линейных уравнений (4) должно выглядеть так, как показано на рисунке 2.5.
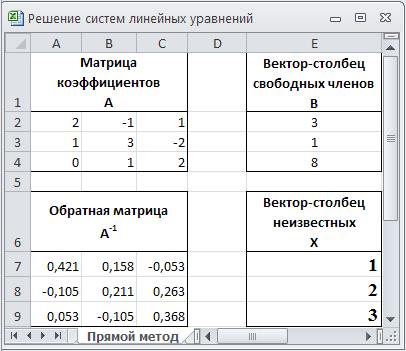
Рис. 2.5. Решение системы линейных уравнений (4) прямым методом
9. Решите систему линейных уравнений (4) итерационным методом. Перейдите на новый рабочий лист и замените его имя. Для этого дважды щелкните левой кнопкой мыши по ярлычку рабочего листа с надписью Лист2 и наберите имя листа Итерационный метод.
10. Матрицу коэффициентов A занесите в ячейки диапазона A2:C4, а вектор-столбец свободных членов B – в ячейки G2:G4, как показано на рисунке 2.6.
11. Сделайте соответствующие надписи и сформируйте выражение для вычисления левой части формулы (2). Для этого в ячейку D2 занесите формулу для вычисления произведения элементов первой строки матрицы A на вектор-столбец неизвестных X
=A2*E$2+B2*E$3+C2*E$4, как показано на рисунке 2.6.
Здесь в формуле используется абсолютная адресация по строкам для того, чтобы при копировании формулы в ячейки диапазона D3:D4, номера строк, в которых расположены значения элементов вектора-столбца свободных членов B, не изменялись.
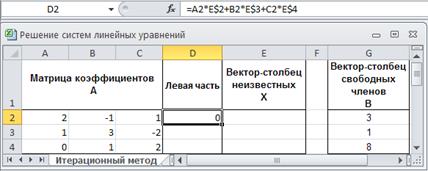
Рис. 2.6. Формула для вычисления левой части выражения (2)
12. Пользуясь маркером заполнения, скопируйте формулу из ячейки D2 в ячейки диапазона D3:D4.
13. В ячейке D5 сформируйте целевую функцию как сумму содержимого ячеек D2:D4. Для этого выделите диапазон ячеек D2:D4 и в группе Редактирование нажмите на иконку 
(Сумма). Вид панели интерфейса Microsoft Excel показан на рисунке 2.7.
Рис. 2.7. Вид панели интерфейса Microsoft Excel после формирования целевой функции
14. В ячейке G5 сформируйте значение целевой функции как сумму содержимого ячеек G2:G4. Для этого выделите диапазон ячеек G2:G4 и в группе Редактирование нажмите на иконку (Сумма). Вид панели интерфейса Microsoft Excel показан на рисунке 2.8.
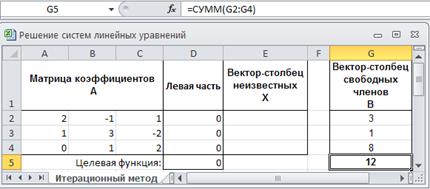
Рис. 2.8. Вид панели интерфейса Microsoft Excel после формирования значения целевой функции
15. На вкладке Файл и выберите команду Параметры, а затем категорию Формулы.
16. Установите флажок Включить итеративные вычисления в положение Включено.
17. Перейдите в категорию Надстройки, в поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти.
18. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения в положение Включено и нажмите кнопку ОК.
19. Перейдите на вкладку Данные и в группе Анализ укажите Поиск решения.
20. В панели Параметры поиска решения установите значения параметров, как показано на рисунке 2.9.
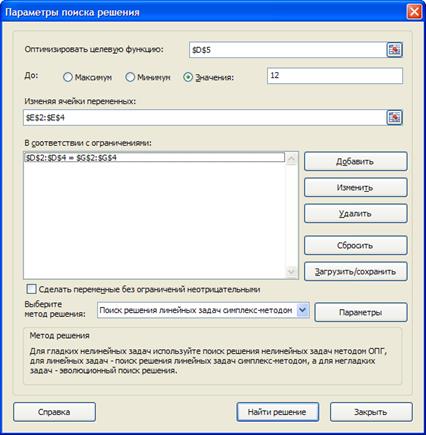
Рис. 2.9. Панель установки необходимых параметров поиска решения
Для этого:
1. В поле Оптимизировать целевую функцию: укажите адрес ячейки, в которую занесена целевая функция D5.
2. Установите переключатель До: в положение З начения:, а в поле ввода занесите значение целевой функции из ячейки G5 равное 12.
3. В поле Изменяя ячейки переменных: укажите диапазон ячеек, в которых будет находится искомое решение E2:E4.
4. В поле В соответствии с ограничениями: с помощью кнопки Добавить занесите ограничения D2:D4=G2:G4.
5. Флажок Сделать переменные без ограничений неотрицательными установите в положение Выключено.
6. В раскрывающемся списке Выберите метод решения: укажите Поиск решения линейных задач симплекс-методом.
21. После установки всех параметров, необходимых для решения системы уравнений, нажмите кнопку Найти решение.
22. В панели Результаты поиска решения изучить полученные результаты и нажать кнопку OK, чтобы сохранить найденное решение, которое должно выглядеть так, как показано на рисунке 2.10.
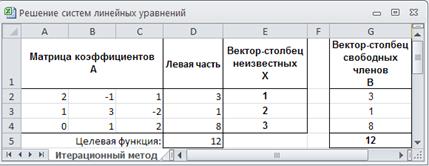
Рис. 2.10. Решение системы линейных уравнений(4) итерационным методом
23. Сравните результаты решения системы линейных уравнений (4) прямым и итерационным методами.
Вывод
Анализ результатов, представленных на рисунках 2.5 и 2.10 показывает, что векторы-столбцы неизвестных X вычисленные прямым и итерационным методами имеют одинаковые значения, следовательно, система (4) решена правильно.
Индивидуальные задания
Найти решение системы линейных уравнений прямым и итерационным методами и сравнить полученные результаты.
1. 
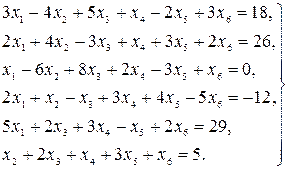
2. 
3. 
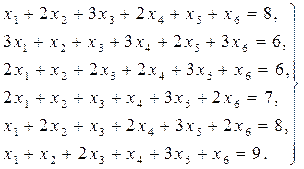
4. 
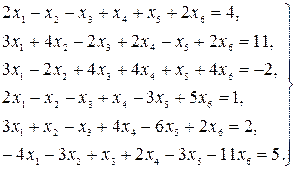
5. 
6. 
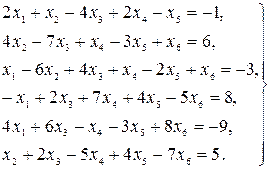
7. 
8. 
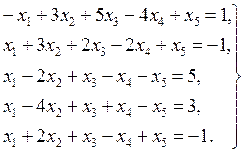
9. 
10. 
11. 
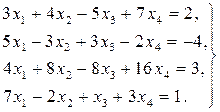
12. 
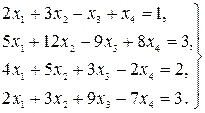
13. 
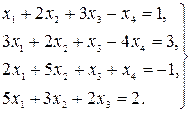
14. 
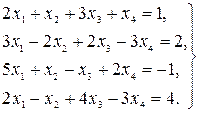
15. 
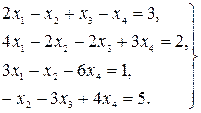
16. 
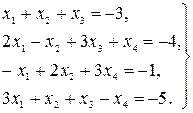
17. 
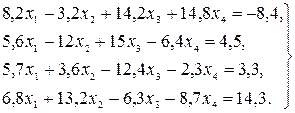
18. 
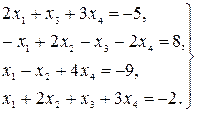
19. 
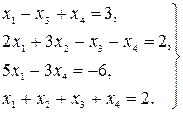
20. 
21. 
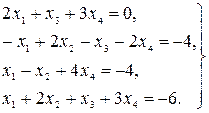
22. 
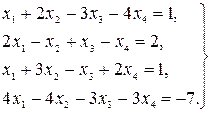
23. 
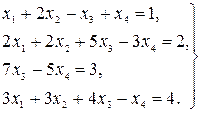
24. 
25. 
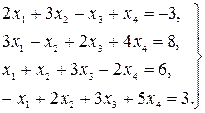
26. 
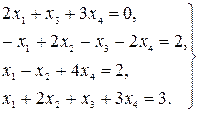
27. 
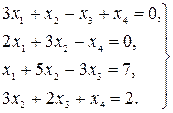
28. 
29. 
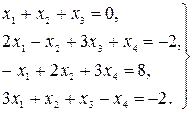
30. 
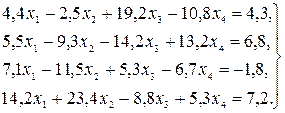
Каждому студенту необходимо выполнить контрольную работу и оформить ее в виде отчета. Отчет должен содержать следующие разделы.
1. Титульный лист, на котором указан вариант индивидуального задания.
2. Название каждой лабораторной работы.
3. Цель работы.
4. Формулировка индивидуального задания.
5. Этапы выполнения задания.
6. Выводы.
Пример оформления титульного листа приведен в Приложении.
Приложение
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ
АГРАРНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Обработка информации средствами электронных таблиц
Контрольная работа
по дисциплине «Информационные технологии»
студентов заочной формы обучения
Вариант №__
Выполнил: студент гр.____
подпись / Фамилия, инициалы/
Проверил:
подпись / Фамилия, инициалы/
Минск
БГАТУ
201_
