Шакирин А. И., Львова О. М.
Обработка информации средствами электронных таблиц
Методические указания для выполнения лабораторных работ
по дисциплине «Информационные технологии»
студентами заочной формы обучения
Минск
БГАТУ
Лабораторная работа №1
ВЫЧИСЛЕНИЕ КОРНЕЙ нелинейных уравнений
С ЗАДАННОЙ погрешНОСТЬЮ
Цель: изучить основные возможности приложения Microsoft Excel 2010 для вычисления корней нелинейных уравнений с заданной погрешностью.
Краткие теоретические сведения
Пусть задана непрерывная функция f(x) и требуется найти все или некоторые корни уравнения
f(x) = 0,(1)
где f(x) алгебраическая или трансцендентная функция. Такая задача довольно часто встречается в практике инженерных расчетов, причем функция f(x) может быть достаточно сложной, и в большинстве случаев получить точные значения корней уравнения (1), как правило, не удается. В этом случае корни уравнения (1) находят приближенно, с заданной погрешностью ε.
Задача вычисления корней нелинейного уравнения с заданной погрешностью ε решается в два этапа. На первом этапе определяется количество, характер, расположение корней и их приближенное значение. На втором этапе приближенные значения корней уточняют с помощью численного метода.
Большинство численных методов основано на последовательном уточнении значения корня от какого-то начального значения x 0 до значения x*, при котором обеспечивается заданная погрешность ε. Каждое повторное уточнение корня называется итерацией. Количество итераций, которое необходимо сделать, заранее не известно и зависит от вида функции f(x), от выбранного итерационного метода, заданной погрешности εи, наконец, удачного выбора начального приближения x 0.
На первом этапе для нахождения начального приближения корня x0 проще всего построить график функции f(x) в окрестности предполагаемого корня a ≤ x 0 ≤ b и найти точку пересечения функции f(x) с осью x. Полученное таким образом начальное приближение x 0 корня используется на втором этапе для вычисления корня x* итерационным методом до получения требуемой точности.
Примеры
1. Найти все действительные корни нелинейного уравнения
 (2)
(2)
с относительной погрешностью ε=10-5.
Методические рекомендации
1. Запустите приложение Microsoft Excel 2010: Пуск → Все программы → Microsoft Office → Microsoft Excel 2010. В окне Excel откроется новая рабочая книга с тремя листами.
2. Сохраните рабочую книгу в своей рабочей папке на диске или на личном внешнем носителе: вкладка Файл – команда Сохранить как. Дайте имя файлу Л.р.№3-пример.
3. Замените имя текущего рабочего листа. Для этого дважды щелкните левой кнопкой мыши по ярлычку рабочего листа с надписью Лист1 и наберите имя листа Пример1.
4. Для удобства поиска начального приближения корня x 0 занесите в ячейки A1, B1 и C1 начальное a, конечное b значения и шаг изменения h=(b-a)/10 аргумента x соответственно, как показано на рисунке 1.1.

Рис. 1.1. Начальное a, конечное b значения и шаг изменения h аргумента x
5. Сформируйте массив значений x. Для этого в ячейку с адресом A2 занесите формулу =A1, а в ячейку с адресом A3 формулу =A2+C$1. Использование абсолютной адресации по строкам в адресе C$1 необходимо чтобы запретить изменение соответствующего адреса при последующем копировании формулы. Затем выделите ячейку A3, наведите курсор мыши на маркер заполнения и протяните его вниз с нажатой левой кнопкой мыши до ячейки с адресом A12 включительно. Массив значений x должен выглядеть так, как показано на рисунке 1.2.
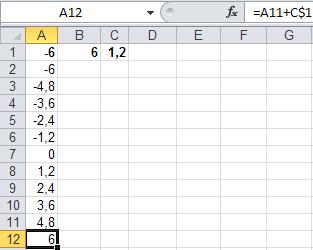
Рис. 1.2. Формирование массива значений x
6. Сформируйте массив значений функции
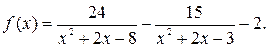 (3)
(3)
Для этого в ячейку с адресом B2 занесите формулу
=24/(A2*A2+2*A2-8)–15/(A2*A2+2*A2-3)–2
Затем выделите ячейку B2, наведите курсор мыши на маркер заполнения и протяните его вниз с нажатой левой кнопкой мыши до ячейки с адресом B12 включительно. Массив значений функции f(x) должен выглядеть так, как показано на рисунке 1.3.
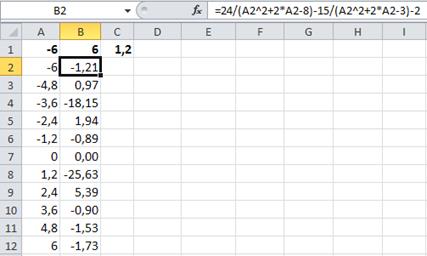
Рис. 1.3. Формирование массива значений функции f(x)
7. Постройте график функции f(x). Для этого выделите диапазон ячеек A2:B12, перейдите на вкладку Вставка, укажите тип диаграммы Точечная и выберите вид Точечная с гладкими кривыми. В построенной диаграмме удалите легенду и горизонтальные линии сетки так, как показано на рисунке 1.4.
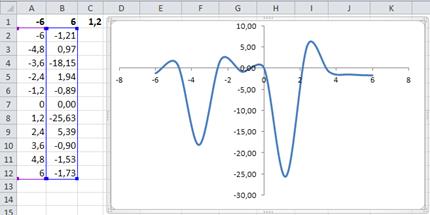
Рис. 1.4. График функции f(x)
Как следует из рисунка 1.4, график функции f(x) пересекает ось x в нескольких точках, следовательно, уравнение (2) имеет несколько корней. Изменяя значения a и b в окрестности предполагаемых корней, определим начальные приближения корней x 0.
8. Занесите в ячейку A1 значение a = - 5,5, а в ячейку B1 значение b = - 4,8, как показано на рисунке 1.5. Примем в качестве начального приближения первого корня x 1 значение - 5 и зафиксируем это значение на рабочем листе.
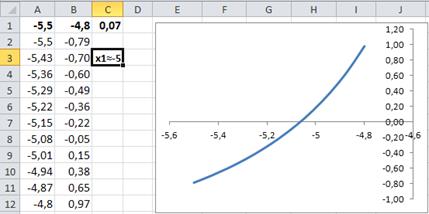
Рис. 1.5. Поиск начального приближения корня x 1
9. Занесите в ячейку A1 значение a = - 2,2, а в ячейку B1 значение b = - 1,5, как показано на рисунке 1.6. Примем в качестве начального приближения второго корня x 2 значение - 2 и зафиксируем это значение на рабочем листе.
10. Занесите в ячейку A1 значение a = - 0,5, а в ячейку B1 значение b = 0,5, как показано на рисунке 1.7. Примем в качестве начального приближения третьего корня x 3 значение 0 и зафиксируем это значение на рабочем листе.

Рис. 1.6. Поиск начального приближения корня x 2

Рис. 1.7. Поиск начального приближения корня x 3
11. Занесите в ячейку A1 значение a = 2,8, а в ячейку B1 значение b = 3,5, как показано на рисунке 1.8. Примем в качестве начального приближения четвертого корня x 4 значение 3 и зафиксируем это значение на рабочем листе.
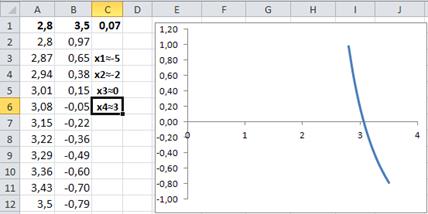
Рис. 1.8. Поиск начального значения корня x 4
Уточните значения корней с заданной относительной погрешностью  . Для уточнения корней используются итерации и надстройка Поиск решения.
. Для уточнения корней используются итерации и надстройка Поиск решения.
12. На вкладке Файл и выберите команду Параметры, а затем категорию Формулы.
13. Установите флажок Включить итеративные вычисления в положение Включено. Значение параметра Предельное число итераций:100 оставьте без изменений, а в поле Относительная погрешность занесите значение 1e-5.
14. Подключите надстройку Поиск решения. Для этого на вкладке Файл в команде Параметры перейдите в категорию Надстройки, в поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти.
15. В окне Надстройки найдите поле Доступные надстройки, установите флажок рядом с пунктом Поиск решения в положение Включено и нажмите кнопку ОК.
16. В ячейку A14 занесите надпись x1, в ячейку B14 занесите найденное начальное значение первого корня - 5, а в ячейку C14 занесите копию ячейки B2 – это целевая функция f(x) выражения (3), так как показано на рисунке 1.9.

Рис. 1.9. Ввод начального значения корня x 1 и целевой функции
17. Перейдите на вкладку Данные и в группе Анализ укажите Поиск решения.
18. В панели Параметры поиска решения установите значения параметров, как показано на рисунке 1.10.

Рис. 1.10. Панель установки необходимых параметров поиска решения
Для этого:
1. В поле Оптимизировать целевую функцию: укажите адрес ячейки, в которую занесена целевая функция C14.
2. Установите переключатель До: в положение З начения:, а в поле ввода занесите значение целевой функции равное 0.
3. В поле Изменяя ячейки переменных: укажите ячейку, в которой будет находится искомое решение B14.
4. Флажок Сделать переменные без ограничений неотрицательными установите в положение Выключено.
5. В раскрывающемся списке Выберите метод решения: укажите Поиск решения нелинейных задач методом ОПГ.
18. После установки всех параметров, необходимых для решения уравнения, нажмите кнопку Найти решение.
19. В панели Результаты поиска решения изучить полученные результаты и нажать кнопку OK, чтобы сохранить найденное решение, которое должно выглядеть так, как показано на рисунке 1.11.

Рис. 1.11. Результат вычисления первого корня x 1 c заданной погрешностью ε=10-5
20. Повторите расчет, задавая в ячейках B15, B16 и B17 начальные значения корней - 2, 0 и 3, соответственно. Полученные результаты должны выглядеть так, как показано на рисунке 1.12.

Рис. 1.12. Результаты вычисления корней нелинейного
уравнения (2) c заданной погрешностью ε=10-5.
2. Найти все действительные корни нелинейного уравнения
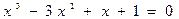 (4)
(4)
с относительной погрешностью ε=10-4.
Корни нелинейного уравнения с заданной погрешностью в некоторых случаях можно вычислить и без графических построений.
1. Замените имя текущего рабочего листа. Для этого дважды щелкните левой кнопкой мыши по ярлычку рабочего листа с надписью Лист2 и наберите имя листа Пример2.
2. На вкладке Файл и выберите команду Параметры, а затем категорию Формулы.
3. Установите флажок Включить итеративные вычисления в положение Включено. Значение параметра Предельное число итераций:100 оставьте без изменений, а в поле Относительная погрешность занесите значение 1e-4.
4. В ячейку A1 занесите надпись x1, в ячейку B1 занесите произвольное начальное значение первого корня, например, - 1, а в ячейку C1 занесите значение целевой функции – левую частьуравнения (4), как показано на рисунке 1.13.

Рис. 1.13. Ввод начального значения первого корня x 1 и целевой функции
5. Перейдите на вкладку Данные и в группе Анализ укажите Поиск решения.
6. В панели Параметры поиска решения установите значения параметров, как показано на рисунке 1.14.

Рис. 1.14. Панель установки необходимых параметров поиска решения
Для этого:
1. В поле Оптимизировать целевую функцию: укажите адрес ячейки, в которую занесена целевая функция C1.
2. Установите переключатель До: в положение З начения:, а в поле ввода занесите значение целевой функции равное 0.
3. В поле Изменяя ячейки переменных: укажите ячейку, в которой будет находится искомое решение B1.
4. Флажок Сделать переменные без ограничений неотрицательными установите в положение Выключено.
5. В раскрывающемся списке Выберите метод решения: укажите Поиск решения нелинейных задач методом ОПГ.
После установки всех параметров, необходимых для решения уравнения, нажмите кнопку Найти решение.
7. В панели Результаты поиска решения изучить полученные результаты и нажать кнопку OK, чтобы сохранить найденное решение, которое должно выглядеть так, как показано на рисунке 1.15.

Рис. 1.15. Результат вычисления первого корня x 1 c заданной погрешностью ε=10-4.
8. В ячейку A2 занесите надпись x2, в ячейку B2 занесите произвольное начальное значение второго корня, например, 0, а в ячейку C1 целевую функцию
 , (5)
, (5)
где  вычисленное значение первого корня, как показано на рисунке 1.16.
вычисленное значение первого корня, как показано на рисунке 1.16.

Рис. 1.16. Ввод начального значения второго корня x 2 и целевой функции
9. Перейдите на вкладку Данные и в группе Анализ укажите Поиск решения.
10. В панели Параметры поиска решения установите значения соответствующих параметров.
11. После установки всех параметров, необходимых для решения уравнения, нажмите кнопку Найти решение.
12. В панели Результаты поиска решения изучить полученные результаты и нажать кнопку OK, чтобы сохранить найденное решение, которое должно выглядеть так, как показано на рисунке 1.17.

Рис. 1.17. Результат вычисления второго корня x 2 c заданной погрешностью ε=10-4
13. В ячейку A3 занесите надпись x3, в ячейку B3 занесите произвольное начальное значение третьего корня, например, 2, а в ячейку C3 целевую функцию
 , (6)
, (6)
где 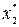 вычисленное значение второго корня, как показано на рисунке 1.18.
вычисленное значение второго корня, как показано на рисунке 1.18.

Рис. 1.18. Ввод начального значения третьего корня x 3 и целевой функции
14. Перейдите на вкладку Данные и в группе Анализ укажите Поиск решения.
15. В панели Параметры поиска решения установите значения соответствующих параметров.
16. После установки всех параметров, необходимых для решения уравнения, нажмите кнопку Найти решение.
17. В панели Результаты поиска решения изучить полученные результаты и нажать кнопку OK, чтобы сохранить найденное решение, которое должно выглядеть так, как показано на рисунке 1.19.

Рис. 1.19. Результат вычисления третьего корня x 3 c заданной погрешностью ε=10-4
18. Попробуйте продолжить процесс поиска корней аналогичным образом и убедитесь в том, что действительных корней уравнение (4) больше не имеет.
19. Подставьте вычисленные корни в уравнение (4) и убедитесь в том, что полученные корни удовлетворяют заданному уравнению.
Индивидуальные задания
Найти все действительные корни нелинейных уравнений с относительной погрешностью 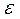 =10-4 двумя методами, рассмотренными в примерах 1 и 2. Сравнить полученные результаты и сделать выводы.
=10-4 двумя методами, рассмотренными в примерах 1 и 2. Сравнить полученные результаты и сделать выводы.
| № | Уравнение | Кол-во корней |
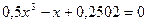
| ||
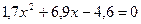
| ||
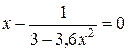
| ||
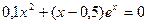
| ||
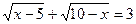
| ||
 
| ||

| ||

| ||

| ||

| ||

| ||
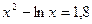
| ||
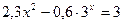
| ||

| ||

| ||
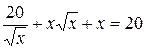
| ||
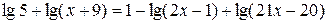
| ||
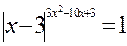
| ||

| ||

| ||
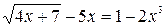
| ||

| ||
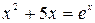
| ||
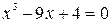
| ||
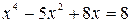
| ||

| ||
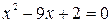
| ||
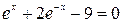
| ||
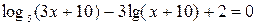
| ||
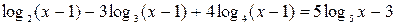
|
Лабораторная работа №2
Решение систем линейных уравнений
Цель: изучить основные возможности приложения Microsoft Excel 2010 для решения систем линейных уравнений.






