Лекция № 2
Функция нескольких переменных
В этой лекции будем говорить только лишь о функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать как правило x и y, а значение функции z.
Будем говорить, что задана функция двух переменных, если любой паре чисел (x, y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие единственное число, которое обозначается f (x, y) и называется значением функции f в точке (x, y).
Множество D называется областью определения функции.
Замечание: поскольку любую пару чисел x, y можно рассматривать как пару координат точки M на плоскости, вместо z = f (x, y) можно писать z = f (M).При этом аргументами функции будут координаты x, y точки M.
Частные производные
Определение: Частной производной по x функции z = f (x, y) в точке M 0(x 0, y 0) называется предел
,
если этот предел существует. Обозначается эта частная производная любым из следующих символов:
; 
; 
.
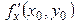Частная производная по x есть обычная производная от функции z = f (x, y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.
Совершенно аналогично можно определить частную производную по y функции z = f (x, y) в точке M 0(x 0, y 0):
= 
.
Приведем примеры вычисления частных производных. Как говорилось выше, для вычисления частной производной по x функции z = f (x, y) нужно положить переменную y равной константе, а при нахождении частной производной по y нужно считать константой переменную x.
Примеры. 1. 
.
2. 
Чаще пользуются более короткими обозначениями:
.
Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y. Они называются вторыми частными производными или частными производными второго порядка и обозначаются zxx ¢¢, zyy¢¢, zxy¢¢ или 
. Согласно определению 
; 
. Последняя частная производная второго порядка называется смешанной.
Экстремум функции двух переменных
Точка M 0(x 0, y 0) является точкой максимума (минимума) функции z = f (x,y), если найдется такая окрестность точки M 0, что для всех точек M (x,y) из этой окрестности выполняется неравенство f (x,y)< f (x 0 ,y 0) (f (x,y)> f (x 0 ,y 0)).
Точки максимума и минимума называются точками экстремума.
Сформулируем необходимое условие существования экстремума: Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.
Замечание: точки экстремума дифференцируемой функции надо искать только среди тех точек, в которых все первые частные производные равны нулю.
Там, где выполняется необходимое условие, экстремума может и не быть (здесь полная аналогия с функцией одной переменной).
Пример: z = xy; zx ¢ = y; zy ¢ = x; zx ¢(0,0) = 0; zy ¢(0,0) = 0.
Обе частные производные в точке (0,0) обращаются в 0. Однако точка (0,0) не является точкой экстремума, так как в ней самой z = 0, а в любой её окрестности есть точки, где z (x,y) > 0 (это точки, лежащие внутри первого и третьего координатных углов), и есть точки, где z (x,y) < 0 (это точки, лежащие внутри второго и четвертого координатных углов).
Для ответа на вопрос, является ли точка области определения функции точкой экстремума, нужно использовать достаточное условие экстремума:
Пусть zx ¢(x 0 ,y 0) = 0 и zy ¢(x 0 ,y 0) = 0, а вторые частные производные функции z непрерывны в некоторой окрестности точки (x 0 ,y 0). Введем обозначения: A = zxx ¢¢(x 0 ,y 0); B = zxy ¢¢(x 0 ,y 0); C = zyy ¢¢(x 0 ,y 0); D = AC - B 2.
Тогда, если D < 0, то в точке (x 0 ,y 0) экстремума нет.
Если D > 0, то в точке (x 0 ,y 0) экстремум функции z, причем если A > 0, то минимум, а если A < 0, то максимум.
Если D = 0, то экстремум может быть, а может и не быть. В данном случае требуются дополнительные исследования.
