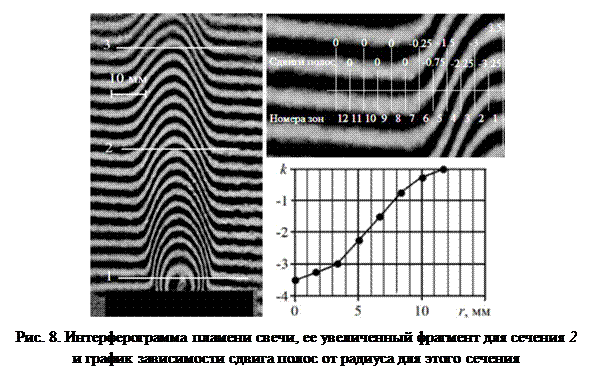
При проведении экспериментов в качестве исследуемого объекта использовалось пламя свечи. Для проведения расчетов было необходимо в выбранном сечении объекта определить сдвиг интерференционных полос относительно их положения при его отсутствии. На интерферограмме (рис. 8) выделены 3 сечения, для которых проводились расчеты. Так как невозмущенные интерференционные полосы не всегда идеально горизонтальны (см., рис. 3, б), определения сдвига полос k проводится следующим образом:
1. Для интерферограмм объекта и невозмущенного поля нумеруются интерференционные полосы (с точностью до постоянного целого числа). Так как плотность (коэффициент преломления) к центру пламени убывает, номер интерференционной полосы в этом направлении тоже должен убывать. Соответственно и для невозмущенного поля выбирается направление возрастания номера интерференционных полос.
 |
2. В выбранном сечении по горизонтальной координате s определяются в общем случае дробные значения номеров невозмущенных интерференционных полос k 01(s).
3. В том же сечении определяются номера интерференционных полос k (s) для пламени.
4. Поскольку положение полос различно для отдельных интерферограмм, с постоянным для всего поля сдвигом ∆ k 0(s) = ∆ k 0 = const, значение ∆ k 0 определяется в невозмущенной области объекта как ∆ k 0 = k 0(s н) ‒ k (s н).
5. Определяется положение полос, которое должно было бы быть без случайной добавки ∆ k 0 для невозмущенного поля k 0(s) = k 01(s) ‒ Δ k 0.
6. Находится k (xs) = k (xs) – k 0(xs).
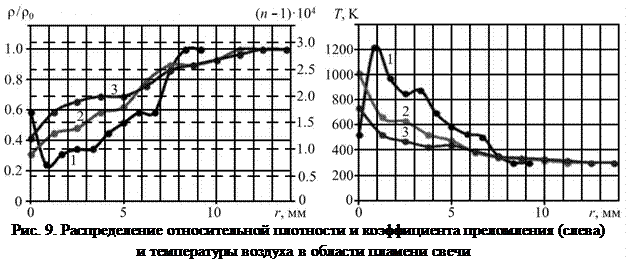
На рис. 8 приведен график сдвигов полос для 2-го сечения. С помощью написанной программы было рассчитано распределение коэффициента преломления и относительной плотности ρ / ρ0 (ρ0 ‒ плотность нормальной атмосферы), а также температуры в пламени свечи для трех сечений (см., рис. 9).
На полученных зависимостях четко наблюдается более высокая температура во фронте горения пламени. Для сечения в области фитиля наблюдается характерный минимум в центре, что соответствует известным экспериментальным данным. В этой области горения еще нет, а нагрев осуществляется в основном за счет теплообмена. Небольшие колебания на графиках, скорее всего, связаны не со структурой исследуемого объекта, а с возможными ошибками в экспериментальных данных. Поскольку задача является условно некорректной, то небольшие сдвиги в экспериментальных данных могут приводить к заметным ошибкам расчета. Но в целом, из полученных результатов и из тестовой задачи видно, что программа работает корректно.
 |
При расчетах предполагалось, что постоянная Гладстона-Дейла, которая различна для разных газов (составов газовых смесей), остается постоянной во всем объеме исследуемого объекта. То есть ее изменения, связанные с наличием продуктов горения, считались пренебрежимо малыми.
Основные результаты
В ходе выполнения работы я ознакомился с интерференционными методами исследования фазовых неоднородностей. Был изучен метод получения интерферограмм с формированием предметного и опорного пучков от отдельных источников. Разработан алгоритм расчета распределения плотности, показателя преломления и температуры в осесимметричных объектах и написана программа для его реализации. Зарегистрированы и обработаны интерферограммы пламени свечи. С использованием созданной программы получены распределения параметров воздуха в пламени свечи для трех сечений. Полученные данные хорошо согласуются с известными результатами других измерений. Полученные результаты предполагается использовать при создании программного приложения, для обработки интерферометрических данных в лабораторной работе по изучению оптической интерферометрии.
Список литературы
1. Бойко В. М., Оришич А. М., Павлов А. А., Пикалов В. В.Методы оптической диагностики в аэрофизическом эксперименте: Монография / Новосибирск: НГУ, 2009. 450 с.
2. Pavlov A. A., Golubev M. P., Pavlov Al. A. Method of phase Heterogeneity Interferogram Registration with a Reference Beam Forming from a Separate Light Source // Proceed. at XII Int. Conference on the Methods of Aerophysical Research. Novosibirsk, 28 June – 3 July, 2004. Novosibirsk, Russia, 2004. Vol. 2. P. 157–161.
3. Островский Ю. И., Бутусов М. М., Островская Г. В. Голографическая интерферометрия. Главная редакция физико-математической литературы издательства «Наука», 1971 г.






