Экспериментальная установка и регистрация интерферограмм

На рис. 2 представлена схема экспериментальной установки. Излучение от гелий-неонового лазера 1 с помощью объективов 2 и коллиматорной линзы 3 формируется в плоскопараллельный пучок, который служит предметной волной. После прохождения исследуемой фазовой неоднородности 4 и собирающей линзы 5 зондирующее излучение подается на регистрирующее устройство, включающее в себя светоделительный кубик 6, гелий-неоновый лазер 7, объектив 8 и приемную телекамеру с объективом 9. Лазер 7 служит источником опорной волны. Принципиально такая схема схожа с интерферометром Маха-Цандера. Однако опорный пучок формируется от отдельного лазера 7, однотипного лазеру 1.

Несмотря на то, что интерференция, как явление, существует всегда, напрямую использование такой схемы не позволяет регистрировать интерференционные картины. Это связано с тем, что излучение любого лазерного источника можно представить в виде отдельных цугов, фазы которых хаотически меняются. Длина среднестатистического цуга определяется длиной когерентности лазера. Поэтому при смене цуга любого из лазеров разность фаз между интерферирующими волнами меняется случайным образом. В результате, за время экспозиции T регистрируется сумма всех интерференционных картин, то есть однородное поле засветки.

Однако если время экспозиции сравнимо или существенно меньше времени когерентности лазерного излучения τ, то можно зарегистрировать интерференционную картину [1], [2]. В нашем случае время экспозиции T = 4 мкс. Время когерентности даже нестабилизированных по частоте генерации гелий-неоновых лазеров составляет, как правило, несколько миллисекунд. Это в принципе позволяет регистрировать интерферограммы с использованием отдельных лазеров для формирования опорной и предметной волн.

Однако ситуация осложняется тем, что частоты излучения даже однотипных лазеров могут отличаться на сотни мегагерц. При несовпадении частот интерферирующих волн на Δν интерференционные полосы будут сдвигаться с фазовой скоростью Δφ / Δ t = 2πΔν. Для регистрации достаточно контрастной для использования интерферограммы, необходимо чтобы за время экспозиции фазовый сдвиг Δφ был существенно меньше 2π. Обычно берут Δφ < π / 2. Это дает для максимальной разницы частот при наших условиях Δν_max < (4 T)^–1 ≈ 65 кГц.

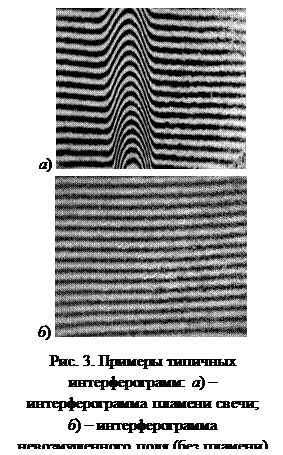
Для соблюдения необходимого условия на разницу частот, регистрация интерферограмм производилась следующим образом. Сначала включался один из лазеров. В результате нагрева резонатора его длина изменяется и, как следствие, меняется частота генерации. Для стабилизации частоты выжидалось 5-10 минут. Затем включался второй лазер, и начинался ввод серии кадров. При прогреве второго лазера частота его излучения так же менялась. Возникали моменты, когда частоты обоих лазеров были достаточно близки друг к другу. При этом на экране монитора отчетливо наблюдались интерференционные полосы. Ввод кадров останавливался. Из серии выбирались значимые кадры, которые в дальнейшем использовались для расчётов. На рис. 3 даны типичные примеры зарегистрированных данным способом интерферограмм.

3. Методика расчетов

Интерферограммы для некоторых типов объектов позволяют получить количественную информацию об изменении показателя преломления. Для газов это дает возможность получать информацию о распределении плотности, поскольку существует линейная связь между изменениями плотности и показателя преломления:

n = 1 + ξρ. (3)

Коэффициент ξ (постоянная Гладсона-Дейла) для разных газов имеет разные значения, но для конкретного газа (газовой смеси) остается постоянным в широком диапазоне температур и давлений.

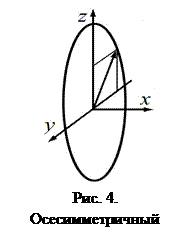
Существует ряд методов по обработке интерферограмм. Они делятся на аналитические и алгебраические. В данной работе использовался алгебраический метод Пирса [3]. Рассматривая симметричное относительно оси x (рис. 4) распределение плотности нагретого воздуха в сечении, найдем сдвиг фазы, используя соотношение (1):

.

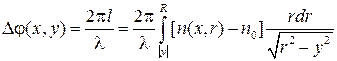Таким образом, сдвиг полос будет равен:

.

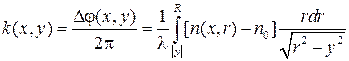Аналитические методы расчетов заключаются в поиске интегрального решения уравнения (2), также называемого интегральным уравнением Абеля. Оно имеет точное решение:

.

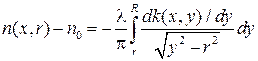Метод Пирса заключается в поиске решения уравнения (2) с помощью системы линейных уравнений. Если разделить сечение на m концентрических колец (см., рис. 5.) одинаковой ширины ∆ r = R / m с центром в области источника пламени, то интеграл можно заменить суммированием:

Рис. 5 поясняет процедуру расчета коэффициентов a_ij. Для упрощения вычисления принято, что l_ij = a_ij / ∆r. Площадь a_ij приблизительно вычисляется как площадь прямоугольника ∆r на l_ij, где l_ij – путь прохождения пучка через соответствующую зону. Можно показать, что:

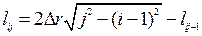. (4)

При i = j и i = 1: 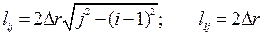. Данное приближение будет работать достаточно точно при разделении на большое количество зон.

В результате, расчет распределения коэффициента преломления сводится к решению системы линейных уравнений:

(5)

Это легко реализуется в программном коде. Если представить систему (5) в матричном виде

AX = B, (5.1)

то решение ищется в виде X = A ^‒1 B. Очевидно, что верхнетреугольная матрица A невырождена в данном случае всегда, а значит, имеет обратную матрицу. Поэтому система разрешима всегда.

Для расчета распределения температуры использовалось уравнение состояния идеального газа в случае постоянного давления для разных температур. Выбор постоянного значения давления обусловлен тем, что в нашем объекте (воздух в области пламени свечи) характерные скорости потока много меньше скорости звука, которая является определяющим параметром для скорости выравнивания давления. В результате имеем:

.

Используя соотношение (3) и учитывая, что n_i = n ₁ + ∆ n_i, получим: 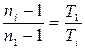, а для температуры i- той зоны .

Описание программы

Программа была написана на языке С++. Часть необходимых данных для проведения расчетов вводится в файл «data.txt» (при запуске консольного приложения выводится инструкция ввода данных). После открытия файла предлагается выбрать метод ввода сдвига полос (загрузить из файла, который нужно создать заранее и ввести имя в консоль, либо ввести сдвиги полос вручную). Полученные в ходе расчетов данные записываются в три текстовых файла («Распределение показателя преломления.txt», «Распределение температуры.txt» и «Распределение плотности.txt») для удобной работы с ними.

Программа позволяет реализовать следующие функции:

1. Для системы (5.1) заполнение матрицы A с использованием формулы (4), вектора B, используя в качестве входных данных количество зон m, длину волны λ, радиус исследуемой области – R и сдвиг интерференционных полос в каждой области k.

2. Нахождение обратной матрицы A ^-1 методом Гаусса.

3. Получение вектора-столбца, состоящего из ∆ n_i,соответствующих каждой зоне, в результате произведения A ^-1 и вектора-столбца B.

4. Расчет распределения коэффициента преломления, температуры и плотности с последующей записью в соответствующие файлы.

Для проверки алгоритма проводился тест. В качестве тестового объекта бралась простейшая математическая модель неоднородности в виде цилиндра. Показатель преломления вне цилиндра n ₀ = 0, внутри цилиндра n = 1. На рис. 6 даны графики распределения коэффициента преломления и сдвига полос в данной модели в зависимости от относительного радиуса r / λ. Для данной модели по сдвигу полос был восстановлен профиль показателя преломления. Тест проводился при разделении исследуемой области на 100 колец. Результаты расчетов полностью совпали с исходным значением показателя преломления. Это доказывает корректность и работоспособности алгоритма.

Целесообразность выбора в качестве тестового объекта цилиндра объясняется тем, что любой осесимметричный объект можно представить в виде суммы соосных цилиндров с положительным или отрицательным изменением показателя преломления (рис. 7). Если программа правильно рассчитывает распределение показателя преломления для отдельного цилиндра, то в силу линейности исходных уравнений, результат будет верен и для всего объекта.

Точность расчетов с использованием данного алгоритма напрямую зависит от количества кольцевых областей m. Чем их больше, тем меньше ошибка итогового результата. Однако в данной работе аналитический анализ ошибок расчета не проводился.