Примеры решения задач
Раздел Физики: Механика
Пример 1. 
Два тела массами m1 = 1 кг и m2 = 2 кг движутся по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях со скоростями v1 = 10 м/с и v2 = 15 м/с соответственно. После соударения первое тело остановилось. Какое количество теплоты выделится при ударе?
Дано: Решение
m1 = 1 кг Поверхность гладкая, значит на систему тел m1 и m2 в горизонталь-
m2 = 2 кг ном направлении внешние силы не действуют и можно воспользо-
v1 = 10 м/с ваться законом сохранения импульса:
v2 = 15 м/с 
, (1)
v´1 = 0 где v – скорость второго тела после удара.
_________ Введем оси x и y, как указано на рисунке и спроецируем на них
Q -? данное векторное уравнение:
OX) m1v1 = m2vx (2)
OY) m2v2 = m2vy, (3)
где vx и vy проекции неизвестной скорости 
.
Найдем их:
; 
(4,5)
Количество теплоты, которое выделится при ударе будет опреде-ляться как разность кинетической энергии системы тел до удара и после удара:
(6)
Ж
Ответ: при ударе выделилось 25 Дж теплоты.
Пример 2. Определить ускорение тела, соскальзывающего с наклонной плоскости, если угол наклона плоскости a =30°, а коэффициент трения между телом и наклонной плоскостью 0,3.
Дано: Решение
a =30° Эта задача на II закон Ньютона, алгоритм решения таких задач известен:
μ = 0,3 1. Расставим силы, действующие на тело:
_______ 
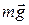- сила притяжения;
а -? 
- сила нормальной реакции опоры;
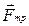- сила трения.
2. Запишем II закон Ньютона в векторном виде:
3. Запишем это уравнение в скалярном виде, спроецировав все векторные величины на выбранные оси. Ось x направим вдоль наклонной плоскости, а ось y – перпендикулярно ей.
OX) mg sin α - Fтр = mа (1)
OY) – mg cos α + N = 0 (2)
Учтем, что Fтр = μ·N (3)
Перепишем уравнения (1) и (2) в следующем виде с учетом (3):
mg sin α − μ·N = mа
mg cos α = N
Подствавив одно уравнение в другое, получим:
mg sin α − μ·mg cos α = mа
Отсюда: α = sin α − μ cos α
α = 0,24 м/с2.
Ответ: α = 0,24 м/с2.
Пример 3. Найти моменты инерции маховика в виде сплошного диска массой 0,5 кг и радиусом 50 см в трех случаях: 1) когда ось вращения проходит через центр масс диска; 2) когда ось вращения параллельна той, которая бы проходила через центр масс диска, но находится на расстоянии 20 см от него; 3) когда ось вращения проходит через точку лежащую на ободе маховика.
Дано: Решение
m = 0,5 кг В первом случае момент инерции находится по известной формуле:
R = 0,5 м I = mR2/2
a2 = 0,2 м I = 0,5·(0,5)2/2 = 0,0625 кг·м2.
a3 = 0,5 м Во втором случае применим теорему Штейнера:
_______ I = Iс + ma2,
а -? где Iс − момент инерции для оси вращения, проходящей через центр масс (мы его рассчитали в задании 1),
a − расстояние от оси вращения до центра масс.
I = 0,0625 + (0,5(0,2)2) = 0,0825 кг·м2.
В третьем случае также применим теорему Штейнера, только расстояние от оси вращения до центра масс будет равно a3 = 0,5 м:
I = 0,0625 + (0,5(0,5)2) = 0,1875 кг·м2.
Ответ: I1 = 0,0625 кг·м2, I2 = 0,0825 кг·м2, I3 = 0,1875 кг·м2.
Примечание: результаты можно округлять до сотых.
Пример 4. Платформа в виде диска массой 200 кг вращается по инерции около вертикальной оси, делая 40 об/мин.В центре платформы стоит человек массой 80 кг. Сколько оборотов в минуту будет делать платформа, если человек перейдет на край платформы? Момент инерции человека рассчитывать как для материальной точки.
Дано: Решение
mп = 200 кг Задача решается с использованием закона сохранения момента
ν1 = 0,67 с-1 импульса: L1 = L2
mч = 80 кг L1 = mпR2/2 · (2π ν1)2
_______ L2 = (mпR2/2 + mч · R2) · (2π ν2)2
ν2 -? где Iп = mпR2/2 − момент инерции платформы, Iч = mч · R2 − момент инерции человека.
Приравнивая оба уравнения и выражая ν2, находим:
_____________ _____________
mп (ν1)2 200 · (0,67)2
ν2 = √ −−−−−−−−−−−− = √ −−−−−−−−−−−−
| mп + 2mч | 200 + 2·80
Ответ: ν2 ≈ 0, 5 с-1.
Раздел физики: Молекулярная физика и термодинамика
Пример 1. Считая радиус каждого капилляра почвы равным 0,3 мм, найти высоту, на которую в них поднимается вода под действием капиллярных сил. Смачивание стенок капилляра считать полным.
Дано: Решение
r = 3·10-4 м Используем уравнение Борелли-Жюрена:
θ = 0° h = (2α cos θ)/ ρgr
ρ = 103 кг/м3 При полном смачивании cos θ = 1. Поэтому уравнение Борелли-Жюрена
α = 72 мН/м примет вид: h = 2α/ ρgr.
_______ h = (2·72·10-3)/ 103 · 9,8 · 3·10-4 ≈ 5 см.
h -? Ответ: h = 5 см.
Пример 2. Длинный, открытый с обоих концов капилляр заполнен водой и поставлен вертикально. Каков радиус капилляра, если высота столба оставшейся в нем жидкости 2 см? (Коэффициент поверхностного натяжения воды 7,4×10-2 Н/м, плотность воды 103 кг/м3, смачивание считать полным).
Дано: Решение
h = 2·10-2 м Используем уравнение Борелли-Жюрена:
θ = 0° h = (2α cos θ)/ ρgr
ρ = 103 кг/м3 При полном смачивании cos θ = 1. Поэтому уравнение Борелли-
α = 7,4×10-2 Н/м Жюрена примет вид:
_______ h = 2α/ ρgr.
r -? Отсюда: r = 2 α/ ρgh.
r = (2·7,4·10-2)/ 103 · 10 · 2·10-2 = 7,4·10-4 м = 0,74 мм.
Ответ: r = 0,74 мм.
Пример 3. Определить градиент плотности углекислого газа в почве, если через площадь 1 м2 ее поверхности за время 1 с в атмосферу прошел газ массой 8×10-8 кг. Коэффициент диффузии 0,04 см2/с.
Дано: Решение
Δs = 1·м2 Используем закон Фика:
Δt = 1 c m = − D·(Δρ/Δx)·Δs·Δt
m = 8·10-8 кг Отсюда: Δρ/Δx = m/ D·Δs·Δt
D = 0,04 см2/с Δρ/Δx = 8·10-8/0,04·1·1 = 2·10-2 кг/м4
_______
Δρ/Δx -? Ответ: Δρ/Δx = 0,02 кг/м4.
Пример 4. Какой путь пройдет жировой шарик диаметром 6 мкм в молоке, плотность которого 1030 кг/м3, за 6 ч? Плотность сливок 900 кг/м3. Коэффициент вязкости молока 1,8·10-3 Па·с.
Дано: Решение
ρм = 1030 кг/м3 Расставим все силы, действующие на всплывающий жировой
ρсл = 900 кг/м3 шарик: сила тяжести (направлена вниз), сила Архимеда (нап-
t = 21600 с равлена вверх), сила Стокса (направлена вниз). На рисунке по-
η = 1,8·10-3 Па·с кажем также вектор скорости и ось у (направлена вверх).
_____________ По второму закону Ньютона в проекции на ось у сумма всех сил,
s -? действующих на тело, равна нулю (движение шарика равномер-ное, ускорение равно нулю):
ОY) FА − mg − FС = 0
Массу можно представить в виде произведения плотности на объем:
m = ρ·V
Объем шарика:
V = 4·π·r3/3
Отсюда, сила тяжести равна:
mg = ρсл·g·4·π·r3/3
Выталкивающая сила (сила Архимеда):
FА = mмg = ρм·g·4·π·r3/3
Сила Стокса:
FС = 6·π·η· r·v
Подставляем все выражения в первую формулу:
6·π·η· r·v = ρм·g·4·π·r3/3 − ρсл·g·4·π·r3/3
Путь, который пройдет шарик равен:
s = v·t
6·π·η· r· s/ t = g·4·π·r3 (ρм − ρсл)/3
Отсюда выражаем s:
s = (2·g·r2·t (ρм − ρсл) /9·η)
s = (2·9,8·9·10-12·21600 (1030 − 900) /9·1,8·10-3) ≈ 0,03 м = 3 см.
Ответ: s = 3 см.
Примечание: к этой задаче рисунок привести обязательно.
Пример 5. Вычислить среднюю энергию поступательного движения молекул азота при температуре 137°С. (84,87×10-22 Дж)
Дано: Решение
Т = 410 К Среднюю энергию поступательного движения молекул азота
найдем по теореме Больцмана:
_____________ Екср = i·k·T/2,
Екср -? где i − число степеней свободы молекул азота.
Число степеней свободы поступательного движения молекул азота равно 3:
i = nпост = 3
k = 1,38·10-23 Дж/К − постоянная Больцмана.
Екср = 3·1,38·10-23·410/2 = 848,7·10-23 = 84,87×10-22 Дж.
Ответ: Екср = 84,87×10-22 Дж.
