Постоянная функция 
(
), степенная 
(
), показательная 
(
, 
), логарифмическая 
(, ), тригонометрические (
, 
, 
, 
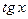) и обратные тригонометрические функции (
, 
, 
, 
) называются простейшими элементарными функциями.
Все функции, получаемые с помощью арифметических действий над простейшими элементарными функциями, суперпозицией этих функций, составляют класс элементарных функций.
1) Функция вида 
(
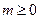, целое; 
, 
– числа) называется целой рациональной функцией или алгебраическим многочленом степени 
. Многочлен первой степени называется также линейной функцией.
2) Функция, представляющая собой отношение двух целых рациональных функций
называется дробно-рациональной функцией. Совокупность целых рациональных и дробно-рациональных функций образует класс рациональных функций.
3) Функция, полученная с помощью арифметических действий и суперпозиций над степенными функциями, не являющаяся рациональной, называется иррациональной функцией.
4) Всякая функция, не являющаяся рациональной или иррациональной называется трансцендентной.
II. Параметрический способ задания функции.
Определение: Параметрической функцией называется функция, у которой каждый аргумент зависит от некоторого параметра, либо от нескольких параметров.
Общий вид параметрической функции от одного параметра с двумя аргументами:
, где 
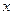и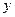 
– координаты произвольной точки 
, лежащей на данной линии, а 
– переменная, называемая параметром (он определяет положение т. 
на плоскости).
Например, если 
, то при 
получаем точку 
. Если параметр изменяется, то точка на плоскости перемещается, описывая линию – такой способ задания функции называется параметрическим. (Механический смысл параметрического уравнения: вследствие того, что точка перемещается по плоскости, уравнения называют уравнениями движения, линию – траекторией точки, при этом есть время).
Определение: Неявной функцией от двух переменных называется функция вида 
, т.е. мы не можем выразить явным образом одну из переменных функции с помощью другой переменной, но мы знаем зависимость между этими переменными.
Примеры неявных функций:
III. Полярные координаты.
Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки на плоскости. Одной из таких систем является прямоугольная (декартова) система координат.
Каждой точке на плоскости ставилась в соответствие пара чисел x и y, называемая ее координатами.
Другой практически важной системой координат на плоскости является полярная. Она задается точкой O, называемой полюсом, лучом Op, называемым полярной осью и единичным вектором 
того же направления, что и луч Op.
Тогда положение произвольной точки (не совпадающей с O) определяется двумя числами: ее расстоянием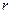 
от полюса и углом 
, образованным отрезком OM с полярной осью (направление против часовой стрелки считается положительным). Числа 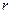и называются полярными координатами точки (полярный радиус и полярный угол).
Обозначение: 
.
Установим связь между прямоугольной и полярной системой координат. Для этого совместим полюс О с началом прямоугольной системы координат, а полярную ось – с положительным направлением оси Ох.
Пусть 
– прямоугольные, 
– полярные координаты точки М, тогда
(из прямоугольного треугольника см. рис)
- определяя величину , следует установить (по знакам x и y) четверть, в которой лежит этот угол и учесть, что 
(или 
).
Вопросы, задаваемые обучающимся:
- Определение функции.
- Способы задания функции.
- Параметрический способ задания функции.
- Как задаются полярные координаты?
Заключительная часть
Итак, мы рассмотрели определение функции, ее свойства, способы задания и основные элементарные функции, ввели понятие полярных координат, рассмотрели параметрический способ занятия функции.
Разработал: 
старший преподаватель кафедры,
капитан вн. службы Е.А. Шварев
«31» июля 2014 года
