Определение передаточных функций САР

Структурная схема САР электропривода постоянного тока строится по уравнениям в операторной форме для отдельных звеньев и представляет собой одну из форм математического описания системы. Исходные урав­нения отдельных звеньев разрешают относительно выходных координат так, чтобы в правой части находилась алгебраическая сумма произведений передаточных функций звена на изображения управляющих и возмущаю­щих воздействий; после этого можно построить структурную схему.

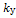
Рисунок 5. Структурная схема САР электропривода постоянного тока.

Построение структурной схемы целесообразно начать с уравнения элемента сравнения, для чего в левой части рисунка стрелками отобража­ются задающее воздействие, приложенное к одному из входов, к другому входу - сигнал обратной связи, приложенный с другим знаком. Это обсто­ятельство подчеркивается затемнением соответствующего сектора в изоб­ражении элемента сравнения.

Далее находим передаточную функцию разомкнутой системы авто­матического регулирования частоты вращения якоря электродвигателя по каналам задающего воздействия () и возмущающего воздействия ().

Передаточная функция по каналу задающего воздействия:

 

 

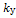
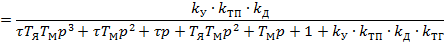
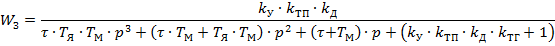
Передаточная функция по каналу возмущения:

 

 

 

 

 

 

 

 

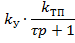
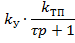
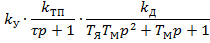
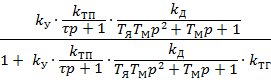
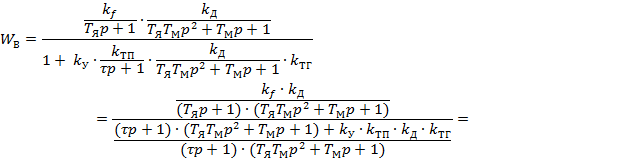
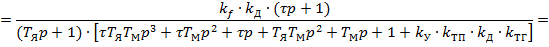
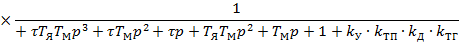
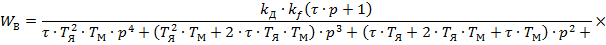
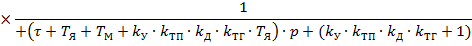
Т_я = L_я / R_я = 0,3/ 0,02 = 15;

;

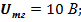
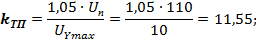
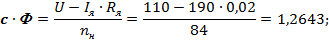
k_д = 1 / с ∙ Ф = 1 / = 0,79096;

Т_м = R_я ∙ J / (c ∙ Ф)² = 0,02·0,3 /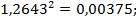

k_ʄ = R_я / c ∙ Ф = 0,02 / = 0,015819;

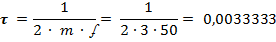
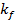
		0,015819	0,79096

Оценка устойчивости

В курсовой работе нужно выполнить оценку устойчивости САР электропривода постоянного тока по критерию Михайлова. При этом необходимо исследовать устойчивость САР электропривода постоянного тока как по каналу задающего воздействия, так и по каналу возмущения.

С помощью критерия Михайлова можно исследовать устойчивость систем автоматического регулирования любого порядка. Представим ха­рактеристическое уравнение разомкнутой автоматической системы в виде:

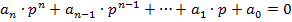
После замены p на 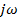получим уравнение комплексного вектора:

 

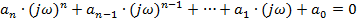
Затем представим его в виде суммы действительной и мнимой составляю­щих:

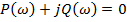
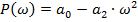
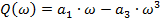
Для устойчивости системы автоматического управления необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от 0 до , начинаясь на вещественной положительной полуоси, обходил против часовой стрелки последовательно п квадрантов координатной плоскости, где п - порядок характеристического уравнения.

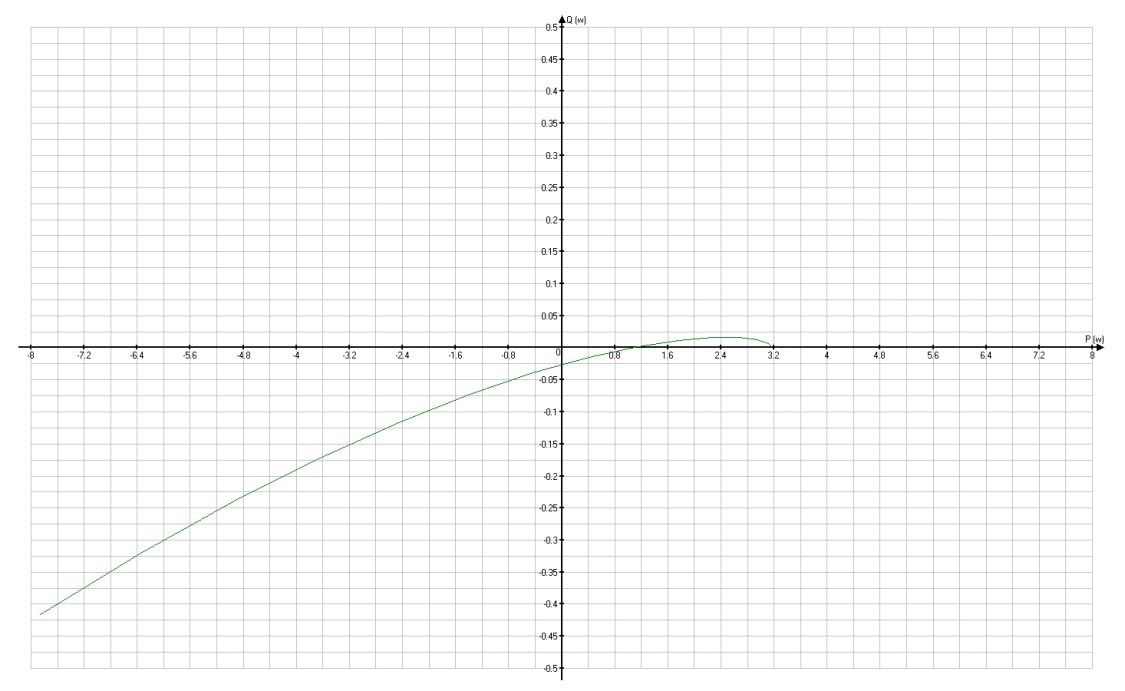
Годограф Михайлова для устойчивых систем имеет плавную спира­левидную форму и уходит в бесконечность в том квадранте, номер которо­го равен степени характеристического уравнения.

По каналу задающего воздействия:

 

 

 

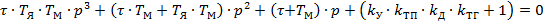
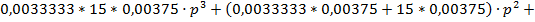
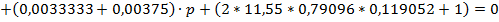
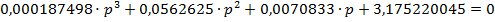
w	P	Q
	3,175141
	3,1188230	0,006899
	2,9498685	0,012673
	2,6682777	0,016194
	2,2740505	0,016336
	1,7671869	0,011975
	1,1476870	0,001982
	0,4155508	-0,01477
	-0,429221	-0,0394
	-1,386630	-0,07304
	-2,456675	-0,11682
	-3,639357	-0,17185

 

 

По каналу возмущения:

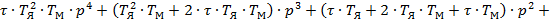
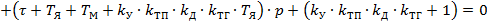
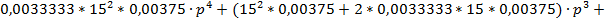
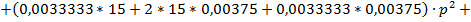
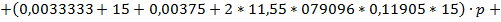
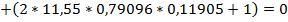
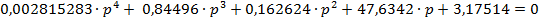
Q(w)

w	P	Q
	3,17514124
	3,01533269	46,78925
	2,56969045	88,50873
	1,93956468	120,0887
	1,29387239	136,4594
	0,86909732	132,551
	0,96929005	103,2938
	1,96606792	43,61807
	4,29861509	-51,546
	8,47368247	-187,268
	15,0655878	-368,618
	24,7162156	-600,666

P(w)

Заключение об устойчивости системы автоматического регулирования электропривода постоянного тока: система автоматического регулирования электропривода постоянного тока будет устойчивой т. к. обе системы устойчивые, потому что имеют плавную спиралевидную форму уходят в бесконечность в том квадранте, номер которого равен степени характеристического уравнения.