Доменная плавка относится к числу непрерывных металлургических процессов, в основу его механизма заложен принцип противотока, что обусловливает высокую экономичность протекающих при этом тепловых и массообменных процессов. Шихтовые материалы (в основном агломерат и кокс), загруженные на колошник доменной печи, медленно движутся вниз (время их пребывания в печи 6 - 12 ч), а им навстречу с довольно большой скоростью (время пребывания порядка нескольких секунд) поднимаются газы, образующиеся в результате сгорания кокса около дутьевых фурм. За это время газы отдают большую часть своего тепла шихтовым материалам и восстанавливают оксиды железа (косвенное восстановление) по схеме:
МеО + СО = Me + СО2;
С02 + С = 2СО.
Восстановлению оксидов металла и снижению температуры плавления материалов способствует также непосредственный контакт кокса с агломератом, особенно по мере приближения к распару и заплечикам, где преобладающим является прямое восстановление:
МеО + С = Me + СО;
МеО + СО = Me + СО2.
Для равномерного распределения газового потока по сечению печи большое значение имеет газопроницаемость сырых материалов. Так как дутье поступает в печь в периферийной области, то газы в первую очередь стремятся подниматься вдоль стенок печи. Для выравнивания сопротивления газовому потоку стремятся загружать печь таким образом, чтобы у стен располагался более толстый слой агломерата, газосопротивление которого больше, чем кокса, а в центральной части находилось больше кокса. Распределение материалов по сечению является важнейшим управлением сверху, действующим, однако, с большим запаздыванием, сравнимым с временем пребывания шихты. Имеются также более быстродействующие управляющие воздействия, направленные снизу. К ним относятся: распределение дутья по фурмам, изменение влажности и температуры дутья, расхода интенсификаторов (кислорода, природного газа или мазута), подаваемых в доменную печь с целью развития процессов косвенного восстановления (в том числе за счет водорода), что приводит к повышению производительности печи и снижению расхода кокса.
Таким образом, даже из приведенной выше краткой характеристики можно видеть, что доменная плавка является очень сложным процессом, распределенным как в пространстве, так и во времени. Математическому описанию этого процесса посвящено большое количество работ. Из-за невозможности сколько-нибудь полного их обзора остановимся лишь на одном достаточно простом примере, удобном с точки зрения пояснения процесса создания модели.
Рассмотрим с этой целью разработанную на заводе Кокура (Япония) модель доменной плавки, предназначенную для использования в системе автоматического управления температурным режимом печи (температурой чугуна).
Прежде чем перейти к конкретным вопросам построения модели следует вспомнить, что процесс моделирования состоит из ряда этапов. Первый из них (постановка задачи), связанный с анализом существующих представлений о процессе и учетом цели, кратко уже рассмотрен выше.
Второй этап состоит из двух ступеней: выбора структурной схемы модели и математического описания ее блоков. При разработке структурной схемы модели были приняты следующие упрощающие допущения:
1) распределение температуры и газового потока по сечению печи равномерное;
2) печь разделена на пять горизонтальных зон, в каждой из которых находятся определенные материалы и протекают соответствующие реакции;
3) сгорание топлива перед фурмами полное, а косвенное восстановление протекает стабильно;
4) находящиеся в каждой зоне материалы остаются неизменными;
5) учитываются только основные компоненты твердой и газообразной фаз;
6) в каждой зоне для твердой и газообразной фаз учитываются только средние температуры.
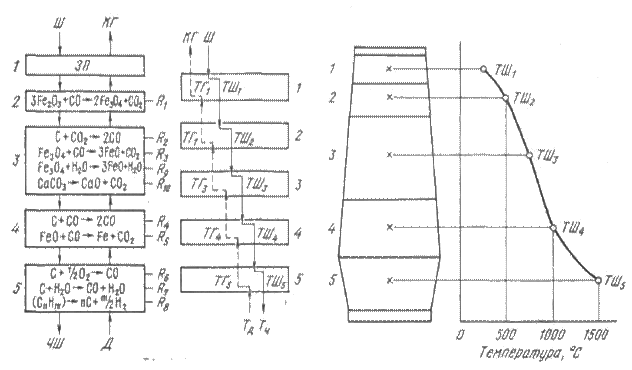Упрощенно структура модели представлена на рис. 3.
Рис. 3. К построению модели теплового состояния доменной плавки
Здесь и в приводимых ниже формулах приняты следующие условные обозначения:
Ш — шихта;
КГ — колошниковый газ;
ЧШ — чугун и шлак;
Д — дутье;
ЗП — зона подогрева;
TШ1 — ТШ5 — температуры шихты но зонам;
TГ1 — ТГ5 — температуры газа по зонам;
i=1,..., 5 — номера зон;
cШi, cГi — средние удельные теплоемкости шихты и газа;
Q Шi, Q Гi — находящиеся в зоне i количества шихты и газа;
vШi, vГi — скорости схода шихты и газового потока;
∆ Нj —- теплота реакции j;
qj — количество тепла, получаемого газом в результате реакции j;
αсi — коэффициент теплопередачи у стенки печи в зоне i;
αрi — коэффициент теплопередачи между газообразной и твердой фазами;
kc, kp — адаптивные коэффициенты теплопередачи;
Rj — скорость реакции j;
Rijx — индекс скорости реакции j в зоне i (если в зоне i протекает реакция j, то Rijx =1, если не протекает, то Rijx = 0);
Рн2М — содержание водорода в мазуте;
Т д, Т ч — температуры дутья и чугуна;
η Н2, — степень использования водорода.
На этапе математического описания ставится задача создания комбинированной (детерминированно-вероятностной) модели. Первая часть ее основана на законах сохранения вещества и энергии, рассмотренных на прошлом занятии. Вторая— на экспериментально-статистических методах (рассмотрим позже).
Составление материального баланса начинается с определения скоростей реакций. Скорость каждой реакции косвенного восстановления (R 1, R 3, R 5 ) выводится из баланса кислорода с учетом допущения 3 (см. выше). Скорость восстановления водородом (R 9 ) и расходование углерода (R 2, γR 4 ) можно вывести соответственно из баланса водорода и углерода, при этом принимается, что R 2 = γR 4. С учетом допущения 3 скорости реакций R 6, R 7, R 8при сгорании топлива перед фурмами определяются непосредственно по параметрам дутья. В результате получена система уравнений скоростей реакций
;
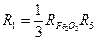R 2 = γ R 4;
;
;
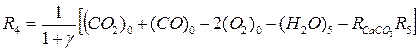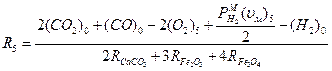; (1)
R 6 = 2 (О 2)5;
R 7 = (Н 2 О)5;
R 8 = (v м)5;
;
.
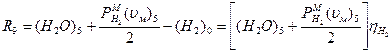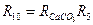По этим уравнениям можно рассчитать скорости реакций R 4, R 5 и R 9 в соответствии с составом колошникового газа.
Учитывая допущение 4, при определении скорости схода шихты и скорости газового потока принимают, что количество шихты и таза на выходе из зоны равно их количеству на входе в зону плюс продукты реакции, т. е.
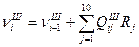; (2)
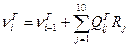. (3)
Изменение энтальпии в каждой зоне обусловлено нарушением теплового баланса; разницей между количествами тепла на входе и выходе зоны, теплот реакций, теплообмена между твердой и газообразной фазами, а также потерь тепла. В связи с этим уравнения теплового баланса для твердой и газообразной фаз в каждой зоне можно записать следующим образом:
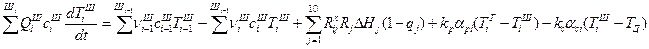. (4)
При расчете теплового баланса для газообразной фазы коэффициент теплопередачи αрi рассчитывался по эмпирической формуле. Эти взаимосвязи можно представить дифференциальным уравнением следующего вида:
, (5)
где Т = (Т1Ш,..., T 5Ш, Т 1Г,..., Т5Г);
С, А — элементы матрицы 10 х 10;
В — вектор-строка 10 х 1.
Так как при стационарном состоянии печи dT/dt = 0, то температуры твердой и газообразной фаз в каждой зоне можно рассчитать по измеряемым параметрам с использованием получаемого в этом случае соотношения Т = В/А. Адаптивные параметры теплопередачи k с и k pвыбираются при этом с помощью итеративной процедуры таким образом, чтобы расчетные температуры Т 1Г и T 5Ш совпадали с фактической температурой колошникового газа и жидкого чугуна. Далее в процессе экспериментальной проверки и использования модели подстраиваются по информации об обратной связи еще несколько параметров, учитывающих, в частности, конкретные условия протекания реакций R 4и R 5и степень использования, например, водорода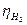 
. Для этого применяются алгоритмы, близкие по смыслу к адаптивным шаговым методам, например вида:
, (6)
где п — число циклов адаптации или управления;
β — подстроечный параметр алгоритма адаптации.
Для возможности использования рассмотренной выше модели [уравнения (1 – 6)] в качестве прогнозирующей в системе управления температурой чугуна необходимо знать динамические характеристики процесса по каналам управляющих воздействий: расходам мазута и кокса, влажности и температуре дутья.
Эта задача может быть сведена к экспериментальному определению зависимостей во времени от упомянутых входных факторов (временных характеристик) скоростей реакций R 4, R 5и температуры чугуна. С использованием методики, эти характеристики аппроксимируются апериодическим звеном первого порядка и чистым запаздыванием и представляются в виде весовой (импульсной) функции следующим образом:
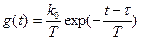, (7)
где τ – интервал времени;
k 0 – коэффициент передачи объекта;
Т – постоянная времени.
В результате для прогнозирующей модели уравнения скоростей реакций R 4 и R 5в системе (1) принимают вид:
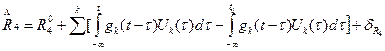, (8)
где R 40— скорость реакции в момент t 0;
U k(τ)— управляющее воздействие k;
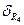— адаптивный член обратной связи, рассчитываемый по соотношению
.
Полученная выше прогнозирующая адаптивная модель [уравнения вида 1 - 7 с уточнениями типа (8)] составляет основу алгоритма системы управления температурой чугуна. Коротко принцип ее работы близок к рассмотренному на рис. 1 и 2. Спрогнозированное с помощью модели значение температуры чугуна с определенным интервалом опережения (например 12 ч) сравнивается с заданным для этого же момента времени. В случае их расхождения путем эксперимента на модели заранее выбираются значения управляющих воздействий, обеспечивающие выполнение задания на прогнозируемый момент времени. Обратная связь по отклонению прогнозируемых с помощью модели выходов от фактических используется для адаптации модели.
Исследование и экспериментальная проверка модели показали возможность прогнозирования температуры чугуна с точностью порядка 5°С, а построенная на основе этой модели система управления позволила существенно снизить расход топлива.
Основная литература
1. Цымбал В.П. Математическое моделирование металлургических процессов: Учебное пособие для вузов. М.: Металлургия, 1986. 240 с.
2. Царегородцев А.В. Математическое моделирование управляющих систем: Учеб. пособие.— М.: Изд-во РУДН, 2003. — 80 с.
Доцент кафедры Автоматизации
технологических процессов металлургии
и машиностроения
А.В. Манкевич
