Вариационное исчисление открыл Леонард Эйлер в первой половине XVIII в., попутно решив для его демонстрации задачу продольного изгиба стержня, и получил известную формулу для критической силы.
Предметом вариационного исчисления является отыскание неизвестных функций 
, реализующих максимум (минимум) или стационарное значение определенного интеграла (функционала).Например:
Если все функции , входящие в функционал, независимы между собой, то вариационная задачи называется свободной, а функционал – полным.
В несвободной вариационной задаче между варьируемыми параметрами имеются зависимости – уравнения связи (дополнительные условия), которые должны быть удовлетворены предварительно, т.е. до варьирования функционала.
Можно совершить переход от несвободной задачи с дополнительными условиями к свободной, используя метод множителей Лагранжа, в соответствии с теорией преобразования вариационных проблем.
Условия, при которых функционал имеет стационарное значение (максимум, минимум), называются (дифференциальными) уравнениями Эйлера и естественными (эйлеровыми ) граничными условиями. Функционал имеет стационарное значение (седловую точку), если 
(здесь имеется в виду вариация функционала по всем независимым переменным). Вопрос о наличии локального экстремума решается знаком второй вариации 
.
Вид уравнений Эйлера зависит от формы математической реализации стационарного значения функционала: аналитической, численной (конечно–разностной), и смешанной.
При аналитической форме уравнения Эйлера могут быть дифференциальными уравнениями с естественными граничными условиями. При численной форме, когда искомые функции отыскиваются в виде сеточных и функционал преобразуется в алгебраическое выражение путем замены интегрирования суммированием, а дифференцирование – численным дифференцированием по соответствующим конечно-разностным формулам, уравнениями Эйлера является система алгебраических уравнений с искомыми значениями в узлах сетки.
Система уравнений и граничных условий линейной ТУ включает:
три статических уравнения:
(7.2)
шесть геометрических уравнений:
(7.3)
шесть физических уравнений:
(7.4)
причем
; 
; 
;
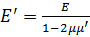статические граничные условия на участках 
:
(7.5)
где 
-направляющие косинусы); 
; 
геометрические граничные условия на участках 
:
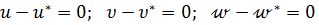(7.6)
Звездочкой отмечены заданные на контуре факторы.
Рассматривается полный функционал линейной теории упругости (7.7), в котором все компоненты векторов напряжений, деформаций и смещений считаются независимыми:
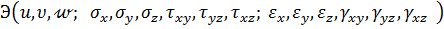(7.7)
Общий вариационный принцип. Истинные поля напряжений, деформаций и перемещений таковы, что полный функционал имеет стационарное значение.
Общая вариационная теорема. Для вариационного принципа , где Э – полный функционал (7.7), уравнениями Эйлера и естественными граничными условиями является весь комплекс статических, геометрических и физических уравнений теории упругости с соответствующими граничными условиями (2 – 6).
Из полного функционала теории упругости как свободной вариационной задачи могут быть получены различные частные функционалы, как несвободные вариационные задачи с дополнительными условиями.
Частные вариационные принципы. Из всех возможных полей напряженно-деформированного состояния упругого тела, удовлетворяющих дополнительным условиям, в действительности имеют место лишь те, которые придают соответствующему частному функционалу стационарное значение.
Частные вариационные теоремы. Для вариационного уравнения 
с некоторыми дополнительными условиями, где 
– частный функционал ТУ, уравнениями Эйлера являются те уравнения и естественные граничные условия, которые в совокупности с упомянутыми дополнительными условиями составляют полный комплекс уравнений и граничных условий ТУ, т.е. уравнений Эйлера и граничных условий для полного вариационного уравнения.
Отсюда следует тождественность постановки задач ТУ на основе полного и частного вариационных уравнений.
Примерами являются частные вариационные принципы Лагранжа, Кастильяно, Рейсснера для граничных условий и др.
Принцип минимума для перемещенийЛагранжа Э(u,v,w) получается, если в качестве дополнительных принять физические (7.4) и геометрические (7.3) уравнения, а также геометрические граничные условия (7.6) на контуре S2, т.е. возможными функциями перемещений u,v,w являются лишь те,которые удовлетворяют указанным дополнительным условиям, а из всех возможных функций перемещений действительными будут те, при которых
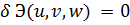. (7.8)
Уравнениями Эйлера для (7.8) будут статические уравнения (7.2) в области V0 и граничные условия (7.5) на участках контура S1.
Принцип минимума для напряжений Кастильяно Э(
) получается, если в качестве дополнительных принять физические (7.4) и статические (7.2) уравнения, а также статические граничные условия (7.5) на участках S1. Из всех возможных, т.е. удовлетворяющих дополнительным условиям функций напряжений , в действительности имеют место лишь те,при которых
Э()=0. (7.9)
Уравнениями Эйлера для (7.9) являются геометрические уравнения в напряжениях и граничные условия (7.6) на S2.
Функционал Рейсснера Э(u,v,w; 
) получается, если в качестве дополнительных принять физические уравнения (7.4).
Если в качестве дополнительных принять все статические, геометрические и физические уравнения (7.2)-(7.4) в области V0, то придем к функционалуграничных условий. Из данного функционала как условия стационарного значения следуют все граничные условия (7.5)-(7.6) на S1 и S2.
О классификации вариационных и разностных методов. Система полного и частных функционалов охватывает все возможные случаи постановки (формулировки) задач ТУ, в т.ч. нерассмотренные смешанные функционалы; взаимосвязь между ними – область математической физики.
Общность и строгость теории полного и частных функционалов может быть положена в основу классификации методов решения задач ТУ. Каждому из функционалов в зависимости от выбора комбинаций искомых функций может быть поставлен в соответствие один или несколько определенных методов расчета, т.е. все методы расчетов являются выражением общей идеи расчленения сложной системы на элементы. В ряде случаев такое расчленение сопровождается механической трактовкой; например, использование в строительной механике основной системы, получаемой из заданной путем наложения или снятия связей, является средством для выполнения дополнительных условий.
Кроме системы функционалов, можно показать связь их с методами аппроксимирующих функций для численного решения краевых задач ТУ. Аппроксимирующие функции подбираются так, что дополнительные условия удовлетворяются точно, а параметры при подходящих функциях – из условий приближенной реализации стационарного значения соответствующего функционала.
В методе Ритца-Тимошенко подходящие функции точно удовлетворяют определенной части граничных и других условий. Оставшаяся часть условий удовлетворяет приближенно с помощью соответствующего функционала (кроме граничных условий).
В методе Бубнова-Галеркина используется преобразованное вариационное уравнение с выделенными вариациями искомых величин. Для правильного конструирования уравнений этого метода в случае некоторых дополнительных условий могут быть использованы соответствующие различные частные функционалы без исключения.
В методе Треффца подходящие функции точно удовлетворяют всем уравнениям в области V0, а функционал граничных условий привлекается для приближенного удовлетворения граничных условий, и т.д.
Метод сеток (метод конечных разностей МКР) универсален, т.к. применим для реализации стационарного значения любого функционала. Дополнительные условия, представленные в конечно-разностном виде, вместе с уравнениями Эйлера в виде сеточных уравнений, составляют разрешающую систему сеточных уравнений. В смешанных методах (вариационно-стержневой, вариационно-разностный), имеющих также вариационное происхождение, сочетаются аналитический и численный подходы в зависимости от области рационального их использования. Например, когда граничные условия на двух противоположных краях трудно описать в виде аналитических подходящих функций, в качестве последних могут использоваться некоторые комбинации аналитических и конечно-разностных функций.
Многоконтактные задачи. Для упругих тел, скрепленных в отдельных точках, линиях, площадках, т.е. для многоконтактных задач, также возможно построение комплекса полного и частных функционалов в соответствии с теорией преобразования вариационных проблем.
Абовским Н.П. выведен комплекс функционалов теории ребристых пологих гибких оболочек и пластинок. Учитывая, что гладкие панели оболочек между ребрами могут иметь различные толщины, в т.ч. и нулевые, постоянные в пределах каждой панели, структура полного функционала составлена так, что выражения функционала для каждого из элементов связаны условиями сопряжения элементов между собой.
Можно показать, что методы строительной механики (методы сил, перемещений, смешанный); система функционалов для строительной механики стержневых систем, предложенная Гольденблатом И.И.; различные варианты метода конечных элементов (МКЭ) исходят из функционала граничных условий многоконтактной задачи. Если расчленить рассматриваемую систему (стержневую или континуальную) на элементы того или иного вида, выполнить сопряжение их в отдельных точках и принять в качестве дополнительных условий статические, геометрические и физические уравнения внутри области каждого из элементов, то в случае линейной задачи достаточно построить матрицы жесткости (податливости) для конечных элементов (КЭ). Решение задачи связано с функционалом граничных условий, из которого следуют в качестве естественных (эйлеровых) граничных условий (если справедлив принцип наложения), алгебраические уравнения классической строительной механики (в зависимости от того, в каких функциях решаются конечные элементы). Если форма, размеры КЭ и связи между ними будут приняты такими, какие по существу имеют место в методе сеток, то данная система КЭ явится механической интерпретацией модели, используемой в методе сеток. При таком подходе по Абовскому Н.П. между методом сеток (МКР) и соответствующим МКЭ не будет существенных различий.
Состояние равновесия или движения деформируемых систем наряду с дифференциальными уравнениями может описываться с помощью рассмотренных вариационных принципов, т.к. положение равновесия консервативной системы есть положение, в котором силовая функция работы всех сил системы имеет минимальное значение.
7.2. Изгиб упругих пластинок. Метод Ритца–Тимошенко
Сущность вариационных методов решения задач теории изгиба пластинок заключается в приведении основного дифференциального уравнения в частных производных С.Жермен-Лагранжа к системе линейных алгебраических уравнений или к обыкновенному дифференциальному уравнению.
Для приведения основного дифференциального уравнения изгиба пластинки к системе линейных алгебраических уравнений, приближенное значение функции прогибов 
можно выбирать в виде ряда с конечным числом членов:
(7.2.1)
где 
- линейные независимые фукции, удовлетворяющие граничным условиям задачи;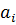 
-- постоянные параметры, подлежащие определению.
В зависимости от числа членов ряда (7.2.1) решение может быть получено с любой степенью точности.
Постоянные параметры 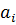выбирают из условий, чтобы функция (7.2.1) по возможности точнее представляла искомую функцию 
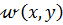. Из различных методов отыскания постоянных параметров 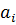рассмотрим два: метод Ритца–Тимошенко и метод Бубнова–Галеркина, которые относятся к прямым вариационным методам.
Метод Ритца первоначально был изложен Рэлеем (Дж. Уильям Стрэтт) для теории звука в 1877 г. и математически обоснован и развит Вальтером Ритцем в 1908 г.; С.П. Тимошенко называет его «метод Рэлея-Ритца», сейчас он больше известен как метод Ритца – Тимошенко.
Метод Ритца–Тимошенко основан на использовании известного из курса теоретической механики принципа возможных перемещений: для того, чтобы система, подчиненная идеальным удерживающим связям, находилось в равновесии, необходимо и достаточно, чтобы сумма элементарных работ всех приложенных к ней сил на всяком возможном перемещении равнялась нулю.
Рассматривая отдельно действие внешних и внутренних сил, принцип возможных перемещений можно представить следующим образом:
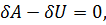(а)
где: 
- возможная работа внешних сил (объемных и поверхностных) на каком-либо возможном перемещении;
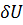- возможная работа внутренних сил, представляющая собой приращение потенциальной энергии на том же возможном перемещении с обратным знаком.
Пусть тело находится в равновесии под действием объемных сил, составляющие которых X, Y, Z, и поверхностных сил 
. Дадим частицам тела возможные перемещения, составляющие которых 
, и подсчитаем работу внешних сил на этих возможных перемещениях. Элементарная работа составляющей объемных сил Х, приходящейся на единицу объема, равна произведению этой силы на объем бесконечного малого элемента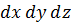 
и на возможное перемещение 
в направлении этой силы:
.
Точно так же элементарные работы составляющих объемных сил Y и Z равны соответственно:
Работа, производимая объемными силами во всем объеме тела V, равна интегралу по этому объему от суммы элементарных работ, совершаемых каждой из составляющих объемной силы:
(б)
Элементарная работа составляющей поверхностных сил 
, которая действует на бесконечно малом элементе поверхности ds, равна произведению равнодействующей этой составляющей на площадке ds на возможное перемещение 
в направлении этой составляющей:
Аналогично определяются и элементарные работы двух других составляющих поверхностных сил:
Работа, производимая поверхностными силами, действующими на всей поверхности тела s, равна интегралу по всей поверхности тела от суммы элементарных работ, совершаемых каждой из составляющих поверхностных сил:
. (в)
Таким образом, возможная работа всех внешних сил на возможных перемещениях равна суме работ объемных (б) и поверхностных (в) сил:
(г)
При вычислении возможной работы внешних сил варьировались только перемещения 
, а поверхностные силы оставалась постоянными, поэтому оператор в формуле (г) можно вынести из-под знаков интегралов, сделав общим для обоих интегралов:
(д)
Приращение потенциальной энергии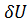 
в формуле (а) подсчитывается согласно интегралу:
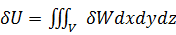, (е)
где 
- удельная потенциальная энергия, определяемая по формуле Клапейрона
W = 
.
Представляя в соотношении (а) оператор общим для обоих слагаемых, получаем:
. (ж)
Выражение, стоящее в скобках, представляет собой работу всех внешних и внутренних сил, приложенных к телу. Эта величина с обратным знаком является потенциальной энергией системы внешних и внутренних сил, действующих на упругое тело:
.(7.2.2)
Вводя это обозначение, вместо условия (ж) получаем следующее соотношение:
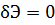. (з)
Так как первая вариация δ с точностью до бесконечно малых величин высшего порядка равна первому дифференциалу, то вместо условия (з) можно написать
,
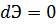а это условие означает, что потенциальная энергия системы Э имеет экстремальное значение.
В курсе теоретической механики доказывается теорема Лагранжа – Дирихле, на основании которой можно сформулировать следующий принцип минимума потенциальной энергии: из всех возможных перемещений упругого тела перемещения, удовлетворяющие условиям устойчивого равновесия, сообщают потенциальной энергии системы минимального значения.
Таким образом, потенциальная энергия системы (7.2.2):
, (7.2.3)
где потенциальная энергия 
, накапливаемая в упругом теле, определяется по формуле, полученной интегрированием по всему объему тела V формулы Клапейрона:
U= 
, (7.2.3а)
а работа объемных и поверхностных 
сил согласно формуле (д):
(и)
При изгибе пластинки объемными силами пренебрегают, а из составляющих поверхностных сил отлична от нуля только одна:
.
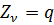Подставляя это выражение в формулу (и) и выбирая элемент поверхности ds в виде прямоугольника со сторонами dx и dy, получаем работу внешних сил при изгибе пластинки:
(7.2.4)
Если приближенное значение функции прогибов выбирать в виде ряда (7.2.1), то после подстановки этого значения в формулу (7.2.3) потенциальная энергия системы окажется функцией параметров :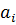
Чтобы найти значения параметров 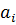, соответствующие минимуму потенциальной энергии системы, нужно приравнять нулю частные производные:
(7.2.5)
Производная квадратичной функции параметров 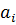оказывается линейной функцией этих параметров, поэтому соотношения (7.2.5) представляют собой систему 
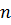линейных уравнений с 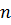неизвестными параметрами .
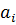Таким образом, метод Ритца–Тимошенко позволяет заменить задачу о нахождении решения дифференциального уравнения С.Жермен-Лагранжа задачей о нахождении минимума потенциальной энергии. Такая замена возможна в связи с тем, что как дифференциальное уравнение изгиба пластинки, так и вариационное уравнение (з) являются уравнениями равновесия упругого тела.
Рассматривая вариационное уравнение (з) в форме
, (к)
внесем в него выражения потенциальной энергии (7.2.3а), формулу приращения удельной потенциальной энергии Клапейрона, а также возможную работу всех внешних сил (г), и учтем, что вариация геометрических уравнений Коши дает
,
……… …… …… ……
,
… ……… ……… …… …..
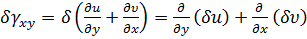В результате преобразований, опущенных из-за громоздкости, получим вместо (з) уравнение, в котором возможные перемещения , 
, 
ничем между собой не связаны; поэтому, чтобы последнее уравнение обращалось в тождество при любых значениях возможных перемещений, должны обращатся в нуль коэффициенты при этих возможных перемещениях. Таким образом, получим шесть уравнений: три уравнения представляют собой статические условия на поверхности в напряжениях(7.5), а три уравнения – дифференциальные уравнения равновесия (7.2). Следовательно, вариационное уравнение (к) заключает в себе дифференциальные уравнения равновесия (7.2) и статические граничные условия (7.5). Отсюда следует, что при использовании вариационного уравнения (к) для приближенного решения задач при выборе функции φi обязательными являются только геометрические граничные условия, а статические граничные условия и дифференциальное уравнение задачи удовлетворяются автоматически.
Таким образом, решение задачи об изгибе пластинки методом Ритца–Тимошенко состоит в следующем. Приближенное значение функции прогибов 
(x,y) выбираем в форме двойного ряда:
(л)
Функции 
должны удовлетворять геометрическим граничным условиям. Вычисляем приближенное значение потенциальной энергии системы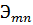 
. Для определения постоянных 
используем систему уравнений (7.2.5), которые в данном случае примут вид
(7.2..6)
Решив эту систему уравнений, найдем параметры ,которые подставим в функцию прогибов (л) и получим приближенное решение задачи об изгибе пластинки.
Следует заметить, что, хотя удовлетворение статических граничных условий в методе Ритца–Тимошенко необязательно, лучше по возможности выбирать функции так, чтобы они удовлетворяли всем граничным условиям, как геометрическим, так и статическим. В этом случае ряд быстрее сходится к точному решению, а при вычислениях бывает достаточно ограничиться одним-двумя членами ряда.
