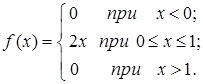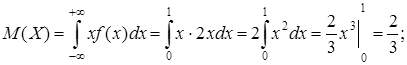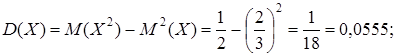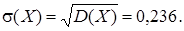Способы задания законов распределения дискретных
Случайных величин
1.1. Случайная величина называется дискретной, если ее значения можно пронумеровать 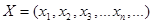 . Она может быть задана рядом распределения, многоугольником или функцией распределения.
. Она может быть задана рядом распределения, многоугольником или функцией распределения.
1.2. Рядом распределения называется совокупность всех частных значений х i и соответствующих им вероятностей 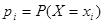 . Ряд распределения оформляется обычно в виде таблицы
. Ряд распределения оформляется обычно в виде таблицы
| xi | x1 | x2 | … | xn | … |
| pi | p1 | p2 | … | pn | … |
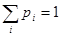
1.3. Многоугольником распределения называется графическое изображение ряда распределения.

1.4. Функцией распределения случайной величины Х называется функция F (x), равная вероятности того, что случайная величина примет значения меньшее выбранного значения, т.е.  . Функция F (x) вычисляется по формуле
. Функция F (x) вычисляется по формуле 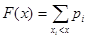 , где суммирование ведется по всем значениям i, для которых
, где суммирование ведется по всем значениям i, для которых  .
.
1.5. Свойства функции распределения
1. F (x) – функция неубывающая.
2.  .
.
3. 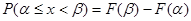 .
.
График имеет вид

Пример 1.1. Составить ряд распределения числа попаданий мячом в корзину при одном броске p = 0,3. Построить многоугольник и функцию распределения.
Решение. Случайная величина Х – число попаданий мячом в корзину при трех бросках. Она может принимать значения 0, 1, 2, 3. Соответствующие вероятности могут быть вычислены по формуле:
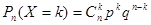 .
.
Этой формулой можно пользоваться, если независимые испытания производятся n раз, вероятность события в каждом испытании постоянна и равна p, a  .
.  – число сочетаний из n по k.
– число сочетаний из n по k.
Здесь 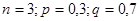 .
.
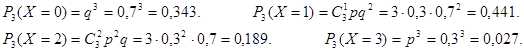
Ряд распределения
| xi | ||||
| pi | 0,343 | 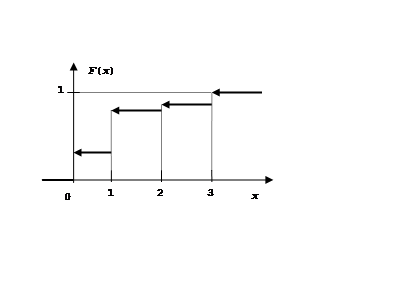 0,441 0,441
| 0,189 | 0,027 |
Многоугольник распределения Функция распределения
 |

Непрерывная случайная величина. Плотность распределения.
2.1. Случайная величина называется непрерывной, если ее функция распределения F (x) непрерывна.
Для описания непрерывных законов распределения чаще используется понятие плотности распределения:
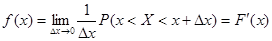 .
.
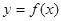 называют также дифференциальной функцией распределения, а ее график – кривой распределения.
называют также дифференциальной функцией распределения, а ее график – кривой распределения.
2.2. Свойства дифференциальной функции распределения.
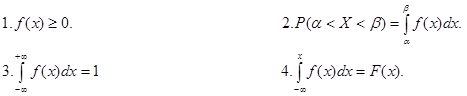
Учитывая свойство (4), функцию F (x) часто называют интегральной функцией распределения непрерывной величины Х.
Пример 2.1. Непрерывная случайная величина имеет интегральную функцию распределения:
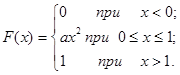
Найти  . Построить графики
. Построить графики  .
.
Решение. По условию задачи функция F (x) непрерывна. При х = 0 разрыва нет.  ;
; 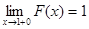 , чтобы при х = 1 не было разрыва, выбираем а = 1.
, чтобы при х = 1 не было разрыва, выбираем а = 1.
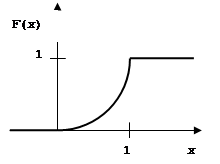
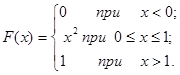
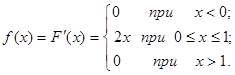

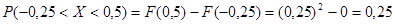 или
или
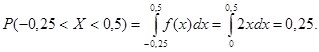
Числовые характеристики случайных величин
3.1. Основные числовые характеристики для дискретных случайных величин определяются по формулам:
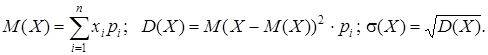
 – математическое ожидание случайной величины Х, которое характеризует среднее значение случайной величины, центр распределения.
– математическое ожидание случайной величины Х, которое характеризует среднее значение случайной величины, центр распределения.  – дисперсия, определяет рассеивание случайной величины около центра.
– дисперсия, определяет рассеивание случайной величины около центра. 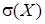 – среднее квадратичное отклонение.
– среднее квадратичное отклонение.
3.2. По аналогии с дискретным распределением математическое ожидание и дисперсия в случае непрерывной случайной определяется формулами:


3.3. Отметим еще формулу, удобную при вычислении дисперсии:
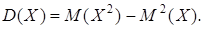
3.4. Свойства математического ожидания и дисперсии
1. 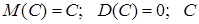 – неслучайная величина.
– неслучайная величина.
2. 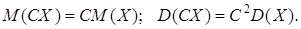
3. 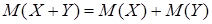 для любых X и Y.
для любых X и Y.
 для независимых случайных величин X и Y.
для независимых случайных величин X и Y.
4. 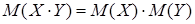 для независимых случайных величин X и Y.
для независимых случайных величин X и Y.
Пример 3.1. Вычислить математическое ожидание и дисперсию случайной величины примера 1.2. 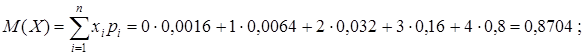
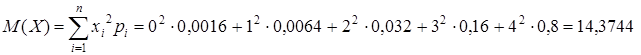
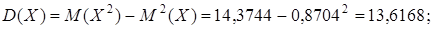
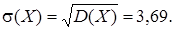
Пример 3.2. Вычислить математическое ожидание и дисперсию для непрерывной случайной величины примера 2.1.