ЛАБОРАТОРНАЯ РАБОТА № 46
«ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА»
Заведующий кафедрой ЕН и ОТД
профессор, к.т.н. А.И. Даутов
Составил: доцент Н.А. Авдонина
г. Кумертау
2015 г.
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
Приборы и принадлежности :
1. Кенотрон типа 2Ц2С на подставке
2. Соленоид
3. Амперметр на 2 А
4. Миллиамперметр на 10 мА
5. Вольтметр на 300 В
6. Реостаты R1, R2, R3, R4
Цель работы: определение удельного заряда электрона методом магнетрона
Краткие теоретические сведения
Непосредственное измерение массы электрона представляет значительную трудность ввиду её малости. Значительно легче определить удельный заряд электрона, т.е. отношение величины заряда к массе e/m, а по величине заряда e и удельное заряду можно найти массу m электрона. Для определения e/m могут применяться различные методы. В данной работе применён метод магнетрона.
Магнетрон представляет собой двухэлектродную электронную лампу с цилиндрическим катодом и коаксиальным с ним цилиндрическим анодом. Лампа помещена в однородное магнитное поле, силовые линии вектора В индукции которого направлены параллельно образующим электродов.
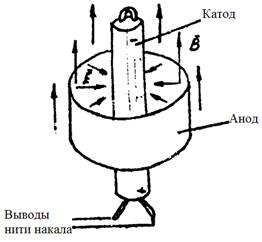
Рис. 1
Катод нагревает нить накала и испускает (эмитирует) электроны. Если к электродам подключить источник питания («+» к аноду, «-» к катоду), то в промежутке между электродами образуется электрическое поле, линии, напряжённости которого будут направлены по радиусу от анода к катоду. При этом на электроны со стороны электрического поля будет действовать сила:
Fк = - eE,
где е — заряд электрона;
Е — вектор напряженности электрического поля. Знак «-» показывает, что заряд электрона — отрицательный.
Изменение кинетической энергии электрона при его движении под действием силы Fк может быть найдено по формуле:
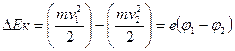, (1)
где φ1, φ2 — разность потенциалов начальной и конечной точек пути;
v1, v2 — начальная и конечная скорости электрона
На электрон, движущийся в магнитном поле, действует сила Лоренца, искривляющая траекторию его движения. Величина и направление силы Лоренца определяется формулой:
Fл = - [ v, В ] Q, (2)
где Fл — вектор силы Лоренца;
v — вектор скорости;
В — вектор магнитной индукции.
На рис.2 показано поперечное сечение магнетрона, где a и b — радиусы катода и анода соответственно. К электродам приложена разность потенциалов. Магнитное поле направлено перпендикулярно чертежу к читателю. На движущийся электрон в точке С действуют силы Fк и Fл. Сила Fк направлена вдоль радиуса к аноду. Сила Fл, согласно формуле (2), перпендикулярна вектору скорости электрона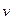 
и вектору индукции магнитного поля В. Направление сил Fк и Fл показано на рис.2. Так как обе силы лежат в плоскости чертежа, движение электрона происходит по плоской спирали переменного радиуса кривизны, зависящего от скорости движения электрона.
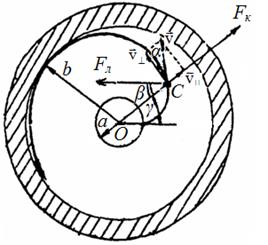
Рис. 2
Для упрощения задачи будем считать, что начальная скорость электрона у катода v = 0.
При В= 0 на электрон действует сила Fк, движение электрона (с учетом Iа= 0) будет прямолинейным вдоль радиуса (рис. 3а). При этом все электроны, эмитируемые катодом, будут достигать анода, создавая анодный ток Iа.
При В> 0 на электрон, кроме силы Fк, будет действовать сила Лоренца Fл, искривляющая траекторию движения электрона. Если В мала, кривизна траектории будет мала, и все электроны будут достигать анода (рис. 3б).
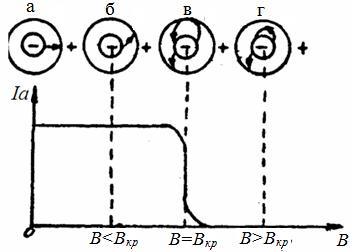
Рис. 3. Зависимость анодного тока магнетрона
от величины индукции магнитного поля
По мере увеличения В траектории будут искривляться все больше и при некотором «критическом» значении В=Вкр траектория электрона окажется касательной к поверхности анода (рис. Зв). При В>Вкр, кривизна траектории станет настолько значительной, что вылетев с катода, электрон будет описывать кривую, заканчивающуюся опять на катоде (рис. 3г). Его скорость в момент возвращения на катод уменьшится до нуля, после чего электрон начнет двигаться к аноду. Поскольку при этом ни один электрон не достигает анода, анодный ток Iа будет равен нулю.
Итак, при В<Вкр величина анодного тока не зависит от В, а при В>Вкр анодный ток вообще прекратится. При В=Вкр, происходит резкий спад (сброс) анодного тока до нуля (рис. Зв). Зная Вкр, можно найти отношение е/m.
Вывод рабочей формулы для расчёта удельного заряда электрона
Будем считать, что В=Вкр и, следовательно, траектория электрона касательна к поверхности анода (рис.2). Введём полярные координаты: радиус-вектор r (r=OC), и угол поворота радиуса вектора φ относительно вертикального направления ОА.
Вектор скорости электрона v можно разложить на составляющую, направленную перпендикулярно к радиусу, и составляющую, направленную вдоль радиуса. Считаем, что при вылете из катода при r= 0, vra = vφa = 0.
При r=b траектория электрона касательна к аноду. Следовательно, vrb = 0, vφb = vb. Для точки касания при r=b можно записать на основании формулы:
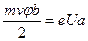, (3)
где Ua — разность потенциалов между анодом и катодом.
Отсюда, находим:
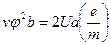. (4)
Для определения е/m этого уравнения не достаточно, т.к. неизвестна величина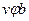 
. Согласно второму закону динамики для вращательного движения имеем:
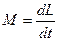. (5)
Момент количества движения электрона в любой момент времени равен:
. (6)
Сила Fе момент не создаёт, т.к. линия её действия проходит через точку О. Поэтому момент силы, действующей на электрон, задаётся только силой Fл (рис.2).
.
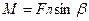Так как, в нашем случае: Fл=еvВкр (см. формулу (2), тогда:
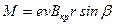. (7)
Из рис. 3 видно, что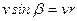 
, поэтому:
. (8)
Произведение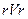 
можно записать так:
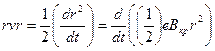. (9)
Тогда из уравнения (5) с учётом (6) и (9) получим:
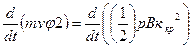. (10)
Это выражение представляет равенство производных двух функций. Т.к. функции, производные которых равны, могут отличаться лишь аддитивной постоянной, можно записать:
mvφr =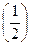 
еВкр r2+С. (11)
Постоянная С может быть определена из начальных условий. При r=0, vφ=0.
Тогда 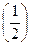еВкра2+С=0, откуда:
С=- 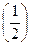еВкра2.
Подставляя значение С в (11), найдём зависимость vφ от радиуса для любой точки траектории:
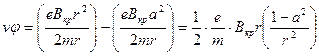. (12)
При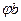 
:
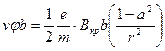. (13)
Возводя vφb в квадрат и подставляя в (4), получим:
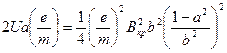. (14)
Из этого квадратного уравнения можно найти е/m. Так как решение е/m= 0 нас не интересует, находим:
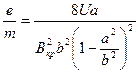. (15)
Описание установки
Установка (рис. 4) представляет собой кенотрон типа 2Ц2С 1, укрепленный на приборной панели клеммными зажимами 3, соединёнными с панелью лампы. На лампу надевается соленоид 4, представляющий собой многослойную катушку 5, намотанную на немагнитном каркасе 6, клеммы 7 служат для питания соленоида.
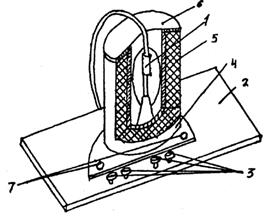
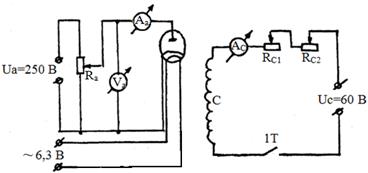
Рис. 4. Вид установки Рис. 5. Принципиальная схема установки
Электрическая схема установки приведена на рис. 5. Она состоит из трех электрических независимых цепей: цепи накала, цепи анода и цепи соленоида. Источником питания двух кенотронных ламп является выпрямитель. Цепь соленоида питается от отдельного селенового выпрямителя. Реостатом Rа и вольтметром Vа поддерживается анодное напряжение. Анодный ток измеряется миллиамперметром mА. Ток в цепи соленоида определяющим величину индукции магнитного поля, устанавливается реостатом Rс2 по амперметру Ас.
Выполнения работы:
1. Ознакомиться с аппаратурой и собранной схемой установки. Определить цену деления каждого прибора.
2. Подать напряжение на источники питания.
3. Включить (тумблером «сеть») источники питания.
4. Прогреть катод в течение 2-3 минут.
5. Подать анодное напряжение Uа1(Uа2) согласно указанного в табл. 1 варианта от универсального источника питания.
Таблица 1
| № варианта | |||||||
| Рекомендуемое анодное напряжение | Ua1 | ||||||
| Ua2 |
6. Увеличивая ток соленоида от сетевого выпрямителя до 2А — через 0,2 А, записывают в таблицу 2 для каждого значения силы тока соленоида Iс соответствующую силу анодного тока Iа.
Ток соленоида от сетевого выпрямителя подается через тумблер 1Т (на приборной панели), имеющий самовозврат. Самовозврат выполнен для защиты катушки соленоида от длительного протекания тока.
Необходимо снять 2 сбросовых характеристики при двух разных анодных напряжениях Uа1 и Uа2 (из таблицы 1).
Таблица 2
| № п/п | ||||||||||||
| Ic | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | ||
| Ua1 | Ia | |||||||||||
| Ua2 | Ia |
7. Снятые сбросовые характеристики построить в виде графиков обязательно на миллиметровой бумаге.
Обработка результатов
Примерный вид сбросовой характеристики показан на рис. 6. По ней можно видеть, что кривая состоит из пяти характерных участков. Такое отличие от рис. 3 объясняются тем, что электроны имеют разброс по тепловым скоростям, так что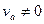 
.
Кроме того, лампа 2Ц 2С, применяемая в работе, имеет форму не цилиндра, а колпачка. Цилиндр с донышком (рис. 7). Поэтому кроме электронов «поперечных», т.е. двигающихся в поперечной плоскости магнетрона, имеются электроны продольные, т.е. двигающиеся параллельно оси или под некоторым углом к ней (рис. 7а).
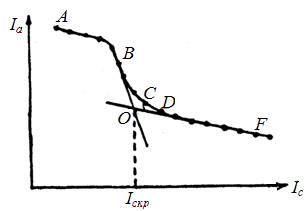
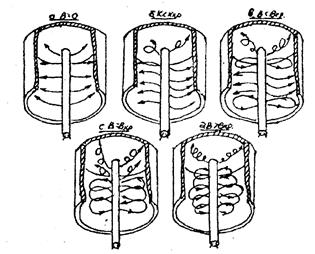
Рис. 6. Вид сбросовой характеристики Рис. 7
Движение электронов в магнетроне
Разберем явления, соответствующие разным участкам кривой (рис. 6):
1. Ход участка А при В<Вкр объясняется тем, что электроны, вылетающие с торца катода, сильно закручивается полем (рис.7 б), т.к. радиус кривизны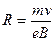 
тем меньше, чем меньше поперечная скорость. В результате образуется пространственный заряд, ослабляющий поле вблизи торца катода и уменьшающий анодный ток в направлении донышка. С ростом В этот заряд должен расти и уменьшать ток Ua.
2. При В <Вкр, но близкой к ней, часть «поперечных» электронов, имеющих максимальные тепловые скорости, закручиваются настолько, что не попадает на анод (участок В). Это и есть начало «сброса» (рис. 7в).
3. Однако при увеличении таких электронов с ростом вблизи цилиндрической части катода образуется пространственный заряд, который будет вытеснять электроны, близкие к торцу катода, в направлении донышка. В результате спад тока становится менее крутым (участок С).
4. При достаточно большом поле В>Вкр будут достигать анода лишь продольные электроны, вылетающие с торца. При этом рост поля приводит к росту пространственного заряда вблизи торца (см. пункт 1) и постепенному уменьшению тока (участок F сбросовой характеристики, рис. 7д).
5. Участок D является переходным от участка С к участку F. Существенные роли в расчёте не имеют, поэтому на основании приведённых рассуждений ток на участке D и F, а также переход участка В с участка С и D обусловлены наличием «прохладных» электронов.
Поэтому пересечение продолжений участков В и F (точка О на рис. 6) соответствует прекращению попадания на анод самых «медленных» «поперечных» электронов, т.е. таких, тепловой скорости, которых близки к нулю (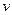
=О). Именно это условие положено в основу при выводе формулы (15). Поэтому Iс будет соответствовать току Iскр для точки О (рис. 7г).
Построение графиков следует делать тщательно. Линии должны быть плавными. Рекомендуемый масштаб по оси ординат — 2 мА в 1 см, по оси абсцисс 0,1-0,2 В в 1 см.
Найдя пересечение участков В и F, опускают перпендикуляр из точки О на ось абсцисс и определяют I скр.
Критическую индукцию магнитного поля находят по формуле:
Вкр=КIскр. (16)
Затем по формуле (15) рассчитывают значения е/m и находят их среднеарифметическое значение. Погрешность величины е/m определяют общим методом, исходя из формулы (15). Погрешность значений Iа, Iс, Uа берут согласно классу точности приборов. Параметры 2Ц2С и погрешность дается ниже: а = (0,095 ± 0,001) см, в = (0,95 ± 0,01) см, К = (0,014 ± 0,001) Тл/а
Контрольные вопросы
1. Что такое удельный заряд электрона?
2. Какие методы измерения удельного заряда Вы знаете?
3. Что называется магнетроном? Как он устроен?
4. Какие силы действуют на электрон в процессе движения в магнетроне и как они направлены?
5. Что такое критическое магнитное поле?
6. Какова форма траектории электрона при В < Вкр, В = Вкр, В > Вкр?
7. Расчётная формула определения удельного заряда электрона методом магнетрона?
8. Чем объяснить, несоответствие экспериментальной и теоретической сбросовых характеристик?
9. Каков тип и класс точности электроизмерительных приборов, применяемых в данной работе? Принцип действия приборов?
10. Какие причины (кроме погрешностей измерительных приборов) могут привести к ошибкам в определении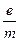 
?
Литература
1. Физический практикум. «Электричество и оптика». В.И. Иверова, «Наука», 1968, стр. 321.
2. «Электричество». С.Г. Калашников. «Наука», 1964, § 98, стр. 201-205.
3. Курс физики. Б.М. Яворский и др. «Высшая школа», 1964, т. II, гл. ХVII, § 18.1, 18.8, 18.4, 18.5.
4. Курс общей физики. Г.А.Зисман и О.М. Тодес. М., «Наука», 1965, т. II, гл. VIII, §36, 37.
