Лабораторна робота №4
Тема: Діофантові рівняння. Застосування конгруенції, їх властивостей та теорем Ейлера і Ферма.
Ціль: навчитись розвязувати Діофантові рівняння першого степеня, визначати остачу від ділення, розвязувати лінійні конгруенції та використовувати їх в прикладних задач цілочисельного розвязку.
Теоретичні відомості
Рівняння виду  , де
, де  - многочлен декількох змінних з цілими коефіцієнтами для яких потрібно знайти цілі розв’язки, називають діофантовими рівняннями. Названі вони ім’ям грецького математика Діофанта, який жив у ІІІ столітті н.е. Його книга «Арифметика» містила 189 задач з цілими числами, для кожної з яких наводилося один або декілька розв’язків.
- многочлен декількох змінних з цілими коефіцієнтами для яких потрібно знайти цілі розв’язки, називають діофантовими рівняннями. Названі вони ім’ям грецького математика Діофанта, який жив у ІІІ столітті н.е. Його книга «Арифметика» містила 189 задач з цілими числами, для кожної з яких наводилося один або декілька розв’язків.
Розв’язати діофантове рівняння означає:
a) з’ясувати, чи має рівняння хоча б один ненульовий розв’язок в цілих числах;
b) якщо рівняння має розв’язок в цілих числах, то з’ясувати скінченна чи нескінченна множина його розв’язків;
c) знайти всі цілі розв’язки рівняння.
Лінійні діофантові рівняння виду 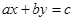 навчились розв’язувати ще до Діофанта. Стародавні греки знали, що якщо це рівняння має один цілий розв’язок
навчились розв’язувати ще до Діофанта. Стародавні греки знали, що якщо це рівняння має один цілий розв’язок  , то його буде задовольняти нескінченна множина пар
, то його буде задовольняти нескінченна множина пар  виду
виду 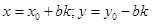 , де
, де  - будь яке ціле число.
- будь яке ціле число.
Математики Стародавньої Греції та Стародавньої Індії знали методи розв’язання деяких рівнянь другого степеня виду 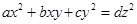 . Зокрема їм були відомі всі піфагорові трійки натуральних чисел
. Зокрема їм були відомі всі піфагорові трійки натуральних чисел  , що задовольняють рівняння
, що задовольняють рівняння  . Всі трійки взаємно простих піфагорових чисел стародавні математики знаходили за формулами
. Всі трійки взаємно простих піфагорових чисел стародавні математики знаходили за формулами 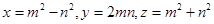 ,
,  - натуральні числа причому
- натуральні числа причому  .
.
Особливе місце серед діофантових рівнянь займає рівняння  , де
, де  - натуральне число. Французький математик П’єр Ферма довів, що при
- натуральне число. Французький математик П’єр Ферма довів, що при  рівняння
рівняння  не має розв’язків в натуральних числах
не має розв’язків в натуральних числах  .
.
Діофантові рівняння першого степеня
Рівняння виду 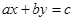 де
де  - числа, а
- числа, а 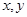 - змінні, називають діофантовим рівнянням першого степеня з двома змінними. Для розв’язання рівняння застосовують наступні теореми.
- змінні, називають діофантовим рівнянням першого степеня з двома змінними. Для розв’язання рівняння застосовують наступні теореми.
Теорема1. Якщо  - взаємно прості числа, то для будь якого цілого
- взаємно прості числа, то для будь якого цілого  , рівняння
, рівняння 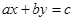 має хоча б один розв’язок в цілих числах.
має хоча б один розв’язок в цілих числах.
Теорема2. Якщо  мають спільний натуральний дільник
мають спільний натуральний дільник  , а ціле число
, а ціле число  не ділиться на
не ділиться на  , то рівняння
, то рівняння 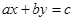 не має розв’язків в цілих числах.
не має розв’язків в цілих числах.
Теорема3. Якщо  взаємно прості числа, то рівняння
взаємно прості числа, то рівняння 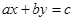 має нескінченну кількість розв’язків
має нескінченну кількість розв’язків 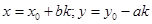 , які знаходять за формулами, де
, які знаходять за формулами, де  - будь який цілий розв’язок даного рівняння,
- будь який цілий розв’язок даного рівняння,  .
.
Частинний розв’язок  можна знайти підбором, для малих
можна знайти підбором, для малих  , а у випадку коли числа
, а у випадку коли числа  великі, то користуємось наступною теоремою.
великі, то користуємось наступною теоремою.
Теорема4. НСД( )
)  може бути записаний у вигляді
може бути записаний у вигляді  , де
, де  цілі числа.
цілі числа.
 знаходимо за алгоритмом Евкліда.
знаходимо за алгоритмом Евкліда.
Означення 1. Цілі числа  і
і  називають конгруентними за модулем
називають конгруентними за модулем 
 , де
, де  — ціле число, якщо їхня річниця
— ціле число, якщо їхня річниця 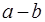 ділиться на
ділиться на  . Позначення:
. Позначення:

Якщо 
 і
і  не конгруентні за модулем
не конгруентні за модулем  , то пишуть
, то пишуть

Означення 2. Цілі числа 
 і
і  називають конгруентними ва модулем
називають конгруентними ва модулем  , де
, де  , якщо еони при діленні на
, якщо еони при діленні на  дають однакові остачі.
дають однакові остачі.
Означення 3. Цілі числа 
 і
і  називають конгруентними за модулем
називають конгруентними за модулем  , де
, де  , якщо існує таке ціле число
, якщо існує таке ціле число  , що
, що  .
.
Означення 1, 2, 3 рівносильні.






