Если интеграл имеет вид 
, то есть в функции присутствует какой-то множитель, который достаточно легко подлежит интегрированию, а в остальном множителе есть явная зависимость от его первообразной, то это значит, что подынтегральная функция есть производная от композиции 
. Тогда можно 
объединить и назвать 
, и далее 
можно будет повсеместно заменить на 
. Рассмотрим, как это действует, на примерах.
Пример. Вычислить 
.
Решение. = 
, фактически здесь уже подготовлена замена 
, более того, дифференциал пересчитывать не нужно, потому что под дифференциалом и так сформировано то же самое, что будет называться . То есть, это частный случай замены переменных, только более простой.
Итак, вид интеграла получается 
= 
.
Сделаем обратную замену, и вот ответ: 
.
Проверка: 
= 
= 
, то есть именно исходную подынтегральную функцию мы и получили.
Интегрирование по частям.
Существует более общий метод, чем подведение под знак дифференциала. Иногда вовсе не требуется, чтобы первообразная от того множителя, который подводится под dx, была как-то связана с остальной частью функции. Запишите формулу:
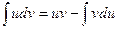
Такой короткий вид легче выучить наизусть, а теперь запишем более подробно, чтобы понять смысл.
.
Если есть два множителя, и один из них интегрируется довольно легко (он обозначен 
) то можно перейти к интегралу, в котором наоборот, 
понижено до производной, а повышено до первообразной. Иногда именно это помогает упростить дальнейшие вычисления.
Доказательство формулы.
Вспомним, что по правилу дифференцирования произведения, которое мы доказывали в прошлом семестре: 
= 
. Тогда 
= 
.
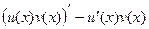Тогда и неопределённые интегралы от этих двух функций совпадают:
= 
.
Но первообразная от производной, это сама функция и есть, т.е.
.
Поэтому = 
.
Пример. Вычислить 
.
Решение. Если обозначить 
, 
, то при переходе к 
степенной понизится степень, в данном случае она вообще перейдёт в 1. А вот для второго множителя переходим к первообразной, но там не усложняется, остаётся точно так же как и было,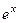 
. Поэтому на следующем шаге интеграл содержит вообще не два множителя, а один!
Составим таблицу:
|
| 
|
|
|
= 
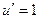
, тогда получаем ответ: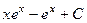 
.
Пример. Вычислить интеграл: 
Составим таблицу:
|
| 
|
|
| 
|
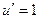
После применения формулы, останется интеграл, в котором всего лишь один множитель, а не два, потому что 
переходит в 1, и один из множителей исчезает.
= 
= 
.
А есть такие случаи, когда функция состоит не из 2 множителей, а всего из одного, но мы ведь всё равно можем считать, что второй множитель есть, только он равен 1.
Пример. 
.
| 
|
| 
|
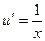
Здесь производная от подынтегральной функции устроена лучше и проще, чем сама функция, но правда, пришлось допустить некоторое незначительное усложнение типа функции при переходе от к 
.
= 
= 
= 
.
