ОСНОВНЫЕ СВОЙСТВА И ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
Электрическое поле (статическое) − поле неподвижных, электрически заряженных тел, заряды которых не изменяются во времени.
Электрическое поле обнаруживается как силовое взаимодействие заряженных тел. При этом различают положительные и отрицательные заряды. Заряды одного знака отталкиваются друг от друга, разного знака притягиваются.
В основе описания свойств электрического поля лежит закон Кулона, установленный опытным путем.
| Закон Кулона. Между покоящимися точечными зарядами действует сила, пропорциональная произведению зарядов, обратно пропорциональная квадрату расстояния между ними и направленная по прямой от одного заряда к другому (рис. 1.1): | ||
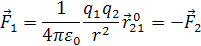
| (1.1) | |
где 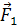 − сила, действующая на заряд
− сила, действующая на заряд 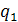 ;
; 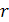 − расстояние между зарядами
− расстояние между зарядами 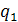 и
и 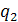 ;
; 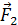 − сила, действующая на заряд
− сила, действующая на заряд 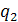 ;
; 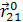 – единичный вектор, направленный от второго заряда к первому;
– единичный вектор, направленный от второго заряда к первому;  – электрическая постоянная.
– электрическая постоянная.
Точечными зарядами можно считать заряженные тела, размеры которых малы по сравнению с расстоянием между ними.
Основная единица измерения силы в международной системе единиц (СИ) − ньютон (Н); заряда − кулон (Кл): 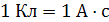 ; длины − метр (м).
; длины − метр (м).
Основными величинами, характеризующими электрическое поле, являются напряженность, электрический потенциал и разность потенциалов, или напряжение.
Напряженностью электрического поля называется мера интенсивности его сил, равная отношению силы 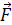 , действующей на пробный положительный точечный заряд
, действующей на пробный положительный точечный заряд 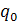 , вносимый в рассматриваемую точку поля, к значению заряда
, вносимый в рассматриваемую точку поля, к значению заряда
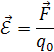
| (1.2) |
Так же как и сила 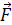 , напряженность электрического поля , напряженность электрического поля 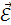 − векторная величина, т.е. характеризуется значением и направлением действия. Основная единица измерения напряженности электрического поля в СИ − вольт на метр (В/м).
Из формулы (1.1) следует, что напряженность электрического поля точечного заряда − векторная величина, т.е. характеризуется значением и направлением действия. Основная единица измерения напряженности электрического поля в СИ − вольт на метр (В/м).
Из формулы (1.1) следует, что напряженность электрического поля точечного заряда 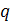 на расстоянии на расстоянии 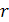 от него равна от него равна
| |
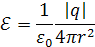
| (1.3) |
и направлена от точки расположения заряда к точке, где определяется напряженность, если заряд положительный (рис. 1.2, а), и в противоположную сторону, если заряд отрицательный (рис. 1.2, б). Если зарядов, создающих электрическое поле, несколько, то напряженность в любой точке поля равна сумме напряженностей от каждого из них в отдельности.
Пример 1.1.
Определить значение и направление действия напряженности электрического поля в точке А, расположенной на расстояниях 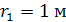 и
и  от точечных зарядов
от точечных зарядов 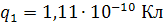 и
и 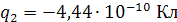 (рис. 1.3).
(рис. 1.3).
Решение. По формуле (1.3) определяем напряженности электрического поля в точке А от действия точечных зарядов 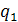 и и 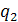
| ||
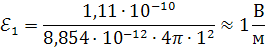
| ||
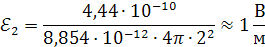
| ||
Направления векторов напряженности 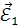 и и 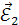 совпадают с направлениями действия сил на пробный положительный точечный заряд, если его расположить в точке А.
Напряженность совпадают с направлениями действия сил на пробный положительный точечный заряд, если его расположить в точке А.
Напряженность 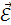 результирующего электрического поля в точке А направлена вдоль гипотенузы прямоугольного треугольника, катетами которого являются векторы напряженностей результирующего электрического поля в точке А направлена вдоль гипотенузы прямоугольного треугольника, катетами которого являются векторы напряженностей 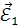 и и 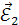 , и имеет значение , и имеет значение

| ||
Можно говорить о поле вектора 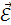 и изображать это поле линиями вектора − силовыми линиями. и изображать это поле линиями вектора − силовыми линиями.
| ||
| Если напряженность электрического поля во всех точках одинакова, то поле однородное, например, поле равномерно заряженной плоской пластины бесконечных размеров (рис. 1.4), а если различна, то поле неоднородно, например поле двух точечных зарядов (рис. 1.5). | ||
| Рис. 1.5 | ||
При перемещении вдоль произвольного участка длиной 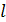 заряда
заряда 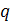 в электрическом поле под действием сил поля
в электрическом поле под действием сил поля 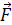 совершается работа
совершается работа
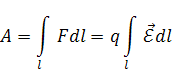
| (1.4) |
При этом работа по переносу заряда вдоль произвольного замкнутого контура равна нулю. Действительно, так как все свойства поля определяются относительным расположением зарядов, то перенос заряда по замкнутому контуру и возвращению в исходную точку означает первоначальные распределение зарядов и запас энергии. Это означает также, что с учетом (1.4) циркуляция вектора напряженности равна нулю
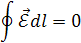
| (1.5) |
Условие (1.5) позволяет характеризовать электрическое поле в каждой точке функцией ее координат − электрическим потенциалом.
Электрический потенциал в данной точке электрического поля
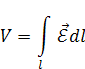
| (1.6) |
с учетом (1.4) численно равен работе, которую могут совершить силы электрического поля при переносе единичного положительного заряда из данной точки в точку, потенциал которой принят равным нулю.
Разность потенциалов двух точек 1 и 2, или напряжение между точками 1 и 2, электрического поля
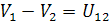
| (1.7) |
численно равна работе, которую могут совершить силы электрического поля при переносе единичного положительного заряда из точки 1 в точку 2.
Единица измерения электрического потенциала в СИ − вольт (В).
Влияние электрического поля на проводники и диэлектрики
Проводниками называются вещества, содержащие заряды, которые могут в них свободно перемещаться (свободные заряды).
К таким веществам относятся, например, металлы (см. табл. 2.1), содержащие свободные электроны, и электролиты, содержащие свободные положительно и отрицательно заряженные ионы.
Диэлектриками называются вещества, в которых свободные заряды отсутствуют. Однако внутри своих электрически нейтральных молекул они содержат связанные между собой положительные и отрицательные заряды. К таким веществам относятся, например, эбонит, гетинакс, асбоцемент и т. д. (см. табл. 1.1 ).
При наличии проводников и диэлектриков электрическое поле существует в том же вакууме, как если бы проводники и диэлектрики отсутствовали, а их влияние на электрическое поле сводится к появлению дополнительных зарядов, переместившихся в
этих веществах под действием электрического поля и в свою очередь создающих электрическое поле.
В проводниках свободные заряды под действием статического электрического поля свободно перемещаются, располагаясь на поверхности проводников. Статическое электрическое поле в проводниках существовать не может, так как в противном случае
было бы перемещение свободных зарядов.
| В диэлектриках под действием электрического поля происходит упругое смещение − поляризация − внутри молекул связанных зарядов (рис. 1.6, положительных зарядов − по направлению поля, отрицательных − в обратном направлении). |
Закон Гаусса. Сумма всех свободных и связанных зарядов, заключенных в объеме, ограниченном замкнутой поверхностью S, пропорциональна потоку вектора напряженности электрического поля через эту поверхность:
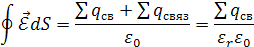
| (1.8) |
где  − относительная диэлектрическая проницаемость диэлектрика (безразмерная величина). Для вакуума
− относительная диэлектрическая проницаемость диэлектрика (безразмерная величина). Для вакуума 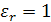 .
.
Произведение относительной диэлектрической проницаемости  на электрическую постоянную
на электрическую постоянную 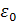 называется абсолютной диэлектрической проницаемостью:
называется абсолютной диэлектрической проницаемостью:
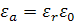
|
Пример 1.2.
Определить напряженность однородного электрического поля равномерно заряженной пластины с плотностью заряда  и разность потенциалов между точками 1 и 2, расположенными на расстояниях
и разность потенциалов между точками 1 и 2, расположенными на расстояниях 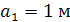 и
и 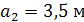 от заряженной пластины вдоль силовой линии поля (см. рис. 1.4).
от заряженной пластины вдоль силовой линии поля (см. рис. 1.4).
Решение. По теореме Гаусса (1.8) поток вектора напряженности электрического поля через поверхность куба с площадью граней S равен
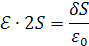
|
откуда
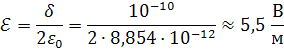
|
Разность потенциалов между точками 1 и 2 по формулам (1.6) и (1.7) равна

|






