және осы арқылы осьтер бойында болатын мүмкін үш орын ауыстыруды жоққа шығарады.
4. Саусақты шарды, ішкі диаметрі берілген шардың диаметріне тең саңлаулы қуыс шарға орналастырып, саусақтың диаметрін саңлаудың еніне тең етіп алсақ, IV кластық кинематикалық жұп (20-сурет) аламыз, бұл кинематикалық жұп звенолардың өз ара салыстырмалы қозғалысына төрт байланыс жасайды, мұнда байланыстар тендеулері мынадай түрде өрнектеледі:
, 
, 
, 
5. Жоғарыда көрсетілгең шар саңлауының ұзындығын саусақ диаметріне дейін қысқартсақ, V кластық кинематикалық жұп (21-сурет) аламыз, мұнда кинематикалық жұп звенолардың өзара салыстырмалы қозғалысына 5 байланыс жасайды, олар мынадай теңдеулермен өрнектеледі:
, , , 
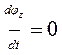
Бұл жағдайда кинематикалық жұп звеноларыньң өз ара салыстырмалы қозғалысы, яғни қалған еркіндік дәрежесінің саны бірге тең, (
) және бұл қозғалыстың кинематикалық теңдеуін былай өрнектеуге болады: 
мұндағы 
— саусақ осіне сәйкес болатын х осін айналу бұрышы.
Өзге звеномен өз ара жанасатын звено элементі (беттер, сызыктар және нуктелер) жанасу формасын анықтайды және жоғарыда көрсетілгендей, жанасу формасына қарай кинематикалық жұптар төменгі және жоғарғы жұпта р болып бәлінеді.
Кинематикалық жұптағы звено элементтерінің арасында тұрақты жанасу болуы қажет. Осындай жанасуды жүзеге асыруды кинематикалық жұптардың тұйықталуы деп атайды.
Тұйықталу геометриялық немесе күштік болады. Бірінші жағдайда тұйықталу кинематикалық жұптардың элементтерінің конструкциалық формалары арқылы жүзеге асырылады да екінші жағдайда звенолардың салмақ күші, арнайы қойылған пружинаның серіпімді күшінің немесе т.б күштердің әсері арқылы жүзеге асырылады.
Қолданылған әдебиеттер:
негізгі:
1. Арустамов Э. А. Оборудование предприятий (торговля): учеб. пособие. М: Дашков и Ко, 2000г.-420с.
2. Электротехника / Под Ред. В.С. Пантюшина М.-Наука и техника 2001 г.-410 с.
3. Борисов Ю.М. Электротехника- М. Наука и техника 1998 г.
4. Кутикович Ф.Г. Электротехника-М. Высшая школа 1999 г.-450 с.
қосымша:
1. Мурзин Ю.М., Волков Ю.И. Электротехника. - СПб.: Питер, 2007. - 443с.
2. Сборник задач по теоретическим основам электротехники. Под редакцией Л.А. Бессонова. - М.:Высшая школа, 2008
3. Атабеков Г.И. Теоретические основы электротехники. - М.: Высшая школа, 2006, ч.1,2,3
Бақылау сұрақтары:
1. Кинематикалық жұп деген не?
2. Байланыс деген не?
ДӘРІС 6
Тақырыбы: Механизмдердің кинематикасы. Механизмдерді кинематикалық зерттеудің негіэгі міндеттері мен методтары
Мақсаты: Механизмдерді кинематикалық зерттеудің негіэгі міндеттері мен методтары.
Дәріс тезистері:
1. Механизмдер кинематикасы
2. Механизмдердіқ кинематикалық анализі
3. Дифференциалдық қисық
Механизмдер кинематикасы уақыт факторын есепке ала отырып, ал әсер етуші күштерді ескермей звенолар мен олардың жеке нүктелерінің қозғалысын зерттейді.
Механизмді кинематикалық зерттеу деп, әдетте, графиктік кескіндеу мен есептеу нәтижесінде әрбІр звеноның орналасу калпын, звено нүктелерінің орын ауыстыруын немесе звенонық бұрылу бұрыштарын, звенолар нүктелерінің сызықтық жылдамдықтарын және үдеулерін, звенолардың бұрыштық жылдамдықтарын және бүрыштық үдеулерІн және механизмнің тағы да басқа кинематикалық параметрлерін анықтайтын процесті айтады.
Звено нүктелерініқ координаталарын, жылдамдықтарын және үдеулерін есептеу механизм жұмысының толық циклінің арасындағы бірқатар орналасу қалыптары үшін жасалады да, мұның өзі механизм нүктелерінің траекториялары мен орын ауыстыру графиктерін құру, жылдамдық пен үдеудің годографтары мен графиктерін жасау сияқты механизм жүмысына дүрыс баға беру үшін қажетті параметрлерді анықтауға мүмкіндік туғызады. Бұл айтылған кинематикалық элементтердің әрқайсысын білу машиналарды зерттеу және конструкциялау үшін қажет. Мысалы,механизм звеноларынық кейбір нүктелерінің траекториялары звеноның жүру жолдарын айқындау, машина корпустарының жобасын жасау үшін, кез келген жағдайда звенолардық орнын еркін ауыстыруына мүмкіндік беру және механизм звеноларынын, бір-бірімен зиянды қақтығысынан сақтау тағы басқалар үшін қажет.
Механизмнің звено нүктелерінің жылдамдығын анықтау, атап айтқанда, машиналардағы жүмыс процесінің жағдайын айқындау үшін қажет. Жьшдамдықты білген соң үдеуді анықтауда болады, ал үдеуді білу арқылы инерция күші мен оның түсу нүктесін табуға болады.
Шапшаң жүретін және ауыр звенолы машиналарда звенолардың қозғалысы біркелкі болмауына байланысты оларда инерция күші үлкен болады, сондықтан олардың беріктігін есептегенде бұл күшті ескеру қажет. Сөйтіп, машина жүмысының сапасын анықтау немесе күш анализі үшін кинематикалық анализ жасау жүмысы жүргізіледі. Онық үстіне кинематикалық анализ машиналардың синетезіне көшу үшін де бір басқыш болып табылады.
Механизмдердіқ кинематикалық анализі үшін графиктік, графоаналитикалық және аналитикалық методтар бар, бұлар жорарғы математика мен теориялық механиканың теоремалары мен ұғымдарына сүйенеді. Механизмдердің кинематикалык анализінің негізгі методтарын түсіндіру үшін механика мен математиканың кейбір қажетті түсініктеріне тоқтала кетейік.
Графиктік диффереициалдау және интегралдау
Графиктік дифференциалдау әдісі абсцисса осі мен қисыққа жургізілген жанама
 |
56-сурет. Жол графигі.
арасындағы бұрыштың тангенсы масштабта сәйкес нүктедегі туынды мәніне тең екендігіне негізделген. Қисықтағы кез келген нүктенің кисықтық центрінің орналасу жағдайы белгісіз болғандықтан, жанама сызықты дәл жүргізу мүмкін емес. Сондықтан практикада хордалар методы деп аталатын графиктік дифференциалдау методы қолданыдады. Бұл:методтың негізін төменгі қарапайым мысалдан байқауға болады.
.Нүктенің s=s(t) графигінің кез келген участогы. берілген делік (56-сурет). Қисыққа аb хордасын жургізгенде пайда болған ас және bc кесінділерін белгілі бір масштабта берілген жол S және уақыт t-ньң өсімшелері деп есептейік, яғни;
мұндағы 
һя — ординаталар (орын ауыстыру — жол) масштабы, м/мм; — 
абсцисса (уақыт) масштабы, сек/мм.
Координаталар системасының бас нүктесінен солға қарай ұзындығы кез келген шамалы полюс қашықтығы деп аталатын Н кесіндісін өлшей отырып, полюс Р-ны табамыз. Полюстен ab хордасына параллель етіп РА сәулесін жүргіземіз. Бұл сәуле А нуктесінде ордината осін киып өтеді. 
ОАР және аЬс үшбұрыштарының ұқсастық қасиеттерінен мынаны аламыз: 
Осыдан 
—орташа жылдамдық, яғни шамалап алғанда, қаралып отырған участоктың орта нүктесіндегі туынды мәні болып табылады. Сонымен РА сәулесінін, ордината осінің бойынан қиған ОА кесіндісі РА сәулесіне параллель хорда керіп түрған участоктағы туындынық орта мәні болып табылады.
Сөйтіп: 
Егер абсцисса.осі бойьнша t уақыт орнына 
бұрылу бұрышы салынған болса, нда
ас болады.
Бұдан: 
Бұл формуладан полюстік қашықтық артқан сайын масштабтық көбейткіштің сан мәні кішірейетінін, яғни дифференциалдық қисықтың графиктік ординаталары артатынын көруге болады. Осы айтылғандарға байланысты төменде графиктік дифференциалдаудың тәртібі баяндалады.
Дифференциалданатын қисықты оның жеке учаскелерінде жүргізілген хордалардан (57-сурет) тұратын сызық сызықпен алмастырамыз.
Графиктік дифференциалдаудың дәлдігін арттыру үшін абсцисса осіндегі бөліктерді әр учаске келеміндегі дифференциалданатын қисық учаскелері мен хордалар мүмкіндігінше бір-біріне неғүрлым жақын болатындай етіп, таңдап алу керек.
Координаталар системасының бас нүктесінен кез келген мөлшерлі Н полюс қашықтығын сол жаққа қарай өлшеп сала отырып, Р полюс нүктесін аламыз. Полюстен ординаталар осіне дейін әр хордаға сәйкес абсцисса осіндегі сәйкес учаскелердін, ортасынан түрғызылған ординаталар етіп аламыз. Осы ординаталардың төбе нүктелері арқылы жүргізілген қисық ізделіп отырған дифференциалдық қисық болады.. Дифференциалдық кисықтың,.шеткі нүкте жағдайлары экстраполяция арқылы анықталады, ол үшін соңғы 0—12 учаскесінен кейін абсцисса осінде, бірінші 0—1 учаскеге тең, қосымша учаске салынады, бүл қосымша учаскенің ортасынан бірінші учаскенің орта ординатасьша тең ордината түрғызылады соңғы және кейін қосылған учаскенін, орта ординаталарының төбе нүктелерін қоса отырып, мөлшері жағынан бастапқы нольдік ординатаға тең келетін шеткі 12-ординатанық шамасын анықтаймыз. Дегенмен, бұл айтылғандарды қолдану үшін диференциалданатын қисық пероидтық қисық болып, 0—12 уақыт интервалы бір толық циклге сай болуыньщ қажет екендіпн атап кетуіміз керек.
Дифференциалдық қисықты чертежге дифференциалданатын кисықпен бірге салуға немесе оны жеке, чертежде басқа жерінде көрсетуге де болады. бойымен қозғалатын нуктенің жылдамдық графигі v=s(t) немесе 
бойынша жоғарыда айтылған методпен үдеу қисығын алуға болады: 
немесе 
Жылдамдықтар қисығының графиктік дифференциалдануы 57-суретте көрсетілген. Егер дифференциалдық қисықты екінші рет дифференциалдаса, онда графиктік дифференциалдауға жіберілген кателіктер көбейе түседі. Сондықтан жазық топсалы механизмдерді кинематикалық анализдегенде графиктік дифференциалдауды екі рет қолдану жөн болмайды.
 |
57-сурет. Жол графигін хорда методымен графиктік дифференцнялдап, жылдамдык және үдеу графиктерш құру.
Графиктік интегралдауды графиктік дифференциалдауға кері бағытта жасаған дұрыс. Қисық 
бойынша оның интегралдық қисығын құру үшін алдымен абсцисса осінен алынған учаскелер ортасынан ординаталар жүргіземіз. Бұл ординаталарды ординаталар осіне көшіреміз. Одан кейін кез келген мөлшерлі полюс қашықтығы Н-ді өлшеп сала отырьш, алынған полюс Р мен ординаталар осіне көшірілген ординаталардық төбе нүктелерін сәулелер арқылы қосамыз. Әрбір учаске келемінде осы сәулелерге параллель кесінділер жүргіземіз.
Бүл кесінділер интегралдық кисықтың хордалары болып табылады. Алынған сынық сызықтар айналасында кисық сызық жүргізіп, іздеп отырған интегралдық кисықты табамыз. Егер бастапқы шарт бойынша интегралдау тұрақтысы нольге тен, болса, онда интегралдық қисық координаталар нүктесінен басталады да, ал нольге тең емес түрақты сан болса, интегралдық қисық шамасы сол сан мөлшеріне тең ордината осіндегі нүктеден басталады. Графиктік интегралдауда қисықтар масштабының ара қатынасы графиктік дифференциалдаудагы қатынас сияқты болады, яғни:
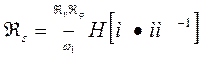
Қолданылған әдебиеттер:
негізгі:
1. Иоффе И.Л. Проектирование процессов и аппаратов химической технологии: Учебник для техникумов. - Л.: Химия, 1991.-352с.
2. Канторович З.Б. Основы расчета химических машин и аппаратов. - М.: Машиностроение, 1960.-744с.
3. Кафаров В.В. Принципы создания безотходных химических производств. - М.: Химия, 1982.-268с.
қосымша:
1. Кузнецов И., Троицкая Т.М. Защита воздушного бассейна от загрезнения вредными веществами химических предприятий. - М.: Химия, 1979.-340с.
Бақылау сұрақтары:
1. Механизмді кинематикалық зерттеу.
2. Механизмдердің кинематикалык анализінің негізгі методтарын түсіндіру үшін механика мен математиканың қажетті түсініктерін айтыңыз.
ДӘРІС 7
Тақырыбы: Жазық фигураның қозғалысы және оның нүктелернің жылдамдықтары мен үдеулері.
Мақсаты: Жазық фигураның орналасу қалпымен және оның нүктелернің жылдамдықтары мен үдеулерімен танысу.
Дәріс тезистері:
1. Жазық фигураның орналасу қалпысы.
2. Вектордың локальдық туындылары
Жазық фигураның орналасу қалпы ОМ кесіндісімен (58-сурет) берілген. ОМ фигурасы I орналасу қалпынан II орналасу калпына ауыстырылды делік. Бүл ауысуды екі бөлікке бөлейік. Әуелі фигураны Ілгерілемелі қозғалыспен V қалыпқа орын ауыстырайық, мүнда берілген фигураньң барлық нүктелері полюс ретінде алынған О нүктесі орын ауыстыратын ОО 1-ге тең қашықтыққа орын ауыстырады,
Ілгерілемелі орын ауыстыру векторы полюсті тандап алуға байланысты, ал Ө бұрылыс бүрышы бұл полюсті таңдап алуға байланысты емес екендігіне көңіл белу қажет.
Жазық фигураның ез жазықтығында кез келген орын ауыстыруын мынадай екі орын ауыстырудың, жиынтығы деп түсінуге болады:
а)полюсті таңдап алуға байланысты ілгерілемелІ орын ауыстыру;
 |
б) полюс айналасында айналу; бұрылу бағыты мен бұрышы полюсті тандап алуға байланысты емес.
58-сурет. Жазық фигураның қозғалысы.
Теориялық механика курсында бұл ереже кез келген шекті орын ауыстыру үшін дәлелденген, ал жеке қаралған шексіз кіші орын ауыстырудың жағдайы үшін векторлық формула беріледі.
58-суретттегі Р-ге тең ММ1} кесіндісі — жазық фигураның I қалыптан II қалыпқа өткендегі М нүктесінің толық орын ауыстыру векторы; алР0-ге тең ММ ' кесіндісі — полюс ретінде алынған 0 нүктеснен бірге М нүктесінің ілгерілемелі ауыспалы орын ауыстыру векторы; ММ1—полюс айналасындағы М нүктесінің салыстырмалы айналмалы орын ауыстыру векторы, сонда P=P0+MM
Егер бұрыш векторы 
болса, онда: 
Бұл формуладан нүктенің толық орын ауыстыру векторы үшін мына формула шыгады: 
формуласының оң және сол бәлігін векторлык дифференциалдағанда жазық фигураның нүкте жылдамдығы үшін мына өрнекті аламыз: 
Қарастырылып отырған М мен О нүктесі — жазық фигураның кез келген нүктелері. Сондықтан жазық фигураның (звеноның) кез келген нүктесінің жылдамдық векторы полюс ретінде алынған А нүктесінің
жылдамдық векторы мен А полюсінің айналасындары В нүктесінің айналу жылдамдығының векторлық қосындысына тең болады, яғни: 
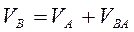
теңдеудің оң және сол бөлігін векторлық дифференциалдап, қарастырылып отырған В нүктесінің үдеу векторы үшін мына векторлык теңдеуді аламыз:
Демек, жазық фигураның (звенонық) кез келген В нүктесінің үдеу векторы 
полюс есебінде алынған (шартты ілгерілемелі козғалыс) А нүктесініц үдеуі 
. және фигураньң полюс маңындағы айналмалы қозғалысындағы (салыстырмалы айналмалы қозғалыс) В нүктесінің үдеу векторының 
қосындасына тең. векторы нормаль 
және тангенциалды үдеу 
векторларынан түрады.
Вектордың локальдық туындылары
Координаталардьң қозғалмайтын системасы ОХУZ -ке қатысты бүрыштық жылдамдығы 
мен айналатын координаталардың қозғалмалы системасы ОХ'У'Z, (59-сурет) және модулі мен бағыты бойынша да өзгеретін вектор а=а (t)- ны қарастырайық. Мүнда вектордьң бағыты координаталардың қозғалмайтын системасы ОХУZ, бойынша да, сондай ақ қозғалатын системасы ОХ'УZ,' бойынша да, өзгеретінін атай кету керек.
а вектордың координаталардың қозғалмалы системасы ОХ'У'Z.'-ке қатысты уақыт бойынша алынған туындысы абсолюттік туынды деп аталады да, 
немесе а таңбасымен белгіленеді.
а вектордың координаталардың қозғалмалы системасы ОХ 1 У 1Z1-ке қатысты уақыт (t) бойынша алынған туындысы салыстырмалы немесе локальдық туынды деп аталады да, немесе а таңбасымен белгіленеді.
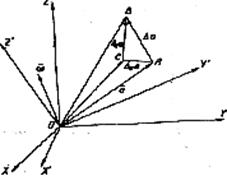
Абсолюттік және локальдық туындылардың арасында тәуелділік орнату үшін
59.сурет. Вектордьщ локальдық туындыларын анықтау.
59суретті қарастырайық, ондағы ОА — t моментіндегі а векторының орны; ОВ — t + 
t моментіндегі а векторының орны; ОС — а векторы әрқашан да қозралмалы системамен өзгеріссіз тәуелділікте болып тұрады деп есептегендегі моментіндегі а векторының орны; АВ = 
а—а векторының абсолюттік өсімшесі; СВ = a қозғалмалы система ОХ'УZ'-ға қатысты а векторьшық өсімшесі (салыстырмалы өсімше);
AC= ea-a — векторын қозғалмалы система ОХ'У'Z' мен әрқашан да өзгеріссіз тәуелділікте болады деп есептелген жағдайдағы қозғалмайтын системаға қатысты а векторының өсімшесі. 59-суреттен мыналарды анық көруге болады:
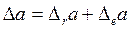
шегі а векторыныд ұшымен дәл келетін ОХ'У'2,' қозғалмалы системасы А нүктесініқңжылдамдығына тең. Жорарыдағы келісім бойынша координаталардың қозғалмалы системасы ОХ'У'2,' қозғалмайтын система ОХУ2-ке қарағанда о лездік бұрыштық жылдамдықпен айналады, сонымен ең соңында алатынымыз:
яғни а векторының (t) уақыт бойынша альнған абсолюттік туыпдысы а векторының салыстырмалы туындысы мен 
вектор шамасының векторлық қосындысына тең.
Қолданылған әдебиеттер:
негізгі:
1. Куркин В.И. Основы расчета и конструирования оборудования электровакуумного производства. Учебн. пособие. - 2-е изд. перераб. и доп. - М.: Высшая школа
2. Москвина И.П. Расчет и конструирование оборудования: Учебн. пособие. М.: МИЭМ
қосымша:
1. Кузнецов И., Троицкая Т.М. Защита воздушного бассейна от загрезнения вредными веществами химических предприятий. - М.: Химия, 1979.-340с.
Бақылау сұрақтары:
1. Жазық фигураның жиынтығы деген не?
2. Жазық фигураның қозғалысы қандай?
ДӘРІС 8
Тақырыбы: Механизмдердің синтезі. Жалпы мәліметтер. Жазық рычагты механизмдердің синтезі.
Мақсаты: Жалпы мәліметтермен жазық рычагты механизмдердің синтезі.
Дәріс тезистері:
1. Негізгі мағлұмат
2. Рычагты механизмдердің синтезі
Пайдасы аз үздікті технологиялық процестердің орнына үнемді, толығынан автоматтандырылған өндіріс өмірге енгізіліп жатқанда технологиялық процестердің же к елеген операцияларын және олардың арасындағы байланысты жүзеге асыруға бағытталған, құрылысы жағынан қарапайым және эксплуатацияда өнімді механизмдердіқ ролі арта түсуде. Соның ішінде звенолары өз ара төменгі II класты 88-сурет.Нуктелердін сызықтык удеулерін знықтау.кинематикалық жүп асайтын үлкен күшті бере алатын және технологиялық жағынан сенімді топсалы-рычагты механизмдер кең өріс алып отыр. Жазық стерженьді төменгі жүпты механизмдер көптеген машиналарда, автоматты линияларда, приборлар мен тетіктерде қолданылуда. Олардын, әр түрлі траекториялар жасауда бағыттауыш механизм есебінде және жетекші звено козғалысының берілген заңын атқаруда үлкен мүм кіндігі бар. Бүл механизмдердің артықшылығы негізінен қүрамына кіретін звенолардық төменгі жұптарымен анықталады, Төменгі жұптардың элементтері беттер болғандықтан, оларда жоғарғы кинематикалық жұптарға қарағанда меншікті қысым мен тозу аз мелшерде болады. Бұл жұптарды жасайтын звено элементтері қарапайым және дәл жасалады, өйткені жазықтықтар мен цилиндр беттерін дәлдікпен өңдеу технологиясы қазіргі күнде өте жақсы жетілдірілген. Топсалы-рычагты механизмдер конструкциялық жағынан қарапайым, эксплуатацияда сенімді, динамикалық жағынан орнықты, тозуға төзімді және жұдырықшалы механизмнен айырмашылығы олардың кинематикалық жүптардын, тұйықталуын туғызатын пружина т. б. тетіктерді қажет етпейтіндігінде. Бұл ерекшеліктер машинаның жетекші білігінің айналу саны және механизм звеноларына түсетін күш шамасы көбейген сайын арта түседі.
Топсалы-рычагты механизмдер, біріншіден, жұмыс звенолары белгілі траектория бойынша күрделі қозғалыста болатын машина-автоматтардың орындаушы механизмі ретінде кеңінен қолданылады, бүларға жалпы машина-автоматтар жатады, екіншіден, топсалы-рычагты механизмдер приборлар мен автоматтық бақылаушы және әр түрлі процестерді басқаратын системаларда функционалды механизмдер ретінде қолданылады.
Рычагты механизмдердің синтезі деп звенолар қозғалыстарынын берілген зандарына байланысты механизм параметрлерін анықтауды айтады. Синтез геометриялық, кинематикалық және динамикалық болып үш түрге бөлінеді.
Геометриялық синтезде жетектегі звеноның берілген қозғалу заңын қамтамассыз ету және берілген траекторияны жасау мәселелері қаралады.
Кинематикалық синтезде звенолардың немесе олардың жеке нүктелерінің жылдамдықтары немесе үдеулерінін берілген шамаларын қамтамасыз ету мәселелері шешіледі.
Динамикалық синтезде механизмдерді жобалау берілген күштерді немесе күштердің беріліс бұрыштарын есепке алу арқылы жүзеге асырылады. Жобаланған механизмнің, жұмыс қабілеті жақсы болу үшін геометриялық синтездің практикалық есептерін шешуде кинематикалық синтездіқ элементтері мен динамикалық синтездің элементтері (күш берілісінің шарттары) ескерілуі кажет.
Төрт звенолы механизмдердің, атап айтқанда, кривошипті-күйентелі механизм, кривошипті-тиекті және кулисалы механизмдерді синтездеу міндеті жиі кездеседі.
Алты звенолы механизмдерді синтездеу сирегірек кездеседі. Көп звенолы механизмдер үшін синтездің арнаулы теориясы жасалмаған.
Синтез есептерін шешу үшін графикік және аналитикалық метод тар қолданылады.
Графиктік методтың, артықшылығы оның қарапайымдылығы мен көрнектілігінде. Аналитикалык метод, графиктік методқа қарағанда, әлдеқайда дәл метод, бірақ онда есептеп шыгару барысында алынатын мәліметтерді бақылап отыруга мүмкіндік тумайды. Сондықтан негізінен синтездің графиктік методын қолданады.
Қолданылған әдебиеттер:
негізгі:
1. Кунву Ли. Основы САПР. ПИТЕР, 2004г.
2. Кондаков А.И. САПР технологических процессов и производств. ACADEMA, 2007
қосымша:
2. Бергхаузер Т., Шлив П. Системы автоматического проектирования AutoCad: Справочник. - М.: Радио и связь, 1989.-256с.
Бақылау сұрақтары:
1. Рычагты механизмдердің синтезі.
2. Динамикалық синтез не арқылы жүзеге асырылады.
ДӘРІС 9
Тақырыбы: Механизмдердің жұмыс істеу қабілеті. Төртінші кластық жазық, рычагты механизмдер синтезі
Мақсаты: Төртінші кластық жазық, рычагты механизмдер синтезі.
Дәріс тезистері:
1. Жоғары кластық жазық рычагты
2. Механизмдердің жұмыс істеу қабілеті.
3. Төртінші кластық жазық, рычагты механизмдер синтезі
Жоғары кластық жазық рычагты механизмдердің екінші және үшінші кластық механизмдермен салыстырғанда берілген қозғалыстарды сапалы түрде іске асырудьң жаңа мүмкіндіктерін тудырады. Осы механизмдердің көмегімен,
мысалы, бір немесе екі жетектеме звенолар үшін звеноның, берілген орын ауыстыруларымен қоса бір немесе екі кідіріс жасайтын есепті шығаруға болады.
Бүл механизмдердің синтезі үшін жазық фигураньң немесе нүктенің екі түрлі қалпының кинематикалық геометрнясын пайдаланған ықғайлы.
Төменде жетекші звеноға және тіреуішке Ассурдың. төртінші кластық әр түрлі ретті структуралық тобын қосудан пайда болган жазық механизмдер синтезінің кейбір есептерінің шешуі келтірілген.
Еесеп. Жетектегі звеносы берілген заң бойынша екі кідіріспен қозғалатын механизмдердің синтезі.
Бүл есепті шығару үшін Ассурдың төртінші кластық екінші ретті тобынан тұратын төртінші кластық механизмніқ схемасын (117-сурет) пайдаланамыз.
Берілген 
және 
(i—1, 2, 3, 4, 5) бүрыштардьщң парымен алғандағы мәндері, жетекші АВ және жетектегі 
звенолардьң орналасу қалыптарын анықтайды, мұнда және 
болады, ол жетектегі звеноның жетекші звеноның 
және 
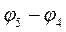бұрышқа бұрылуына сәйкес берілген уақыт аралығындағы екі үзілісін анықтайды.
Шешуі. 1. Екі еркіндік дәрежесі бар АВСDЕ кинематнкалық тізбектің звеноларынын, өлшемдерін және бастапқы қалпын ескереміз. ТІзбектің бастапқы
 |
жағдайы
және 
бұрыштары арқылы анықталады.17-сурет. Төртінші кластық екінші ретті Ассур тобынан тұратын
төртінші кластық механизмінің схемасы
2. Берілген 
және - 
- бұрыштармен анықталатын АВ және ДЕ
звеноларының, берілген пар-парымен алъшғандағы жағдайларын саламыз. Кідірістер болу үшін 
және деп алу керек.
3. Қозғалысты кері айналдыру әдісі бойынша Е нүктесі арқылы өз ара тең, бірақ ДЕ звеноның - бурыштық орын ауыстыруларына қарсы бағытталған айналу қозғалысын береміз. Бұл жағдайда ДЕ звеносы қозғалмайтын звено болады, А және С нүктелері радиустары ЕА және ДС болатын шеңберлер бойымен орын ауыстырады, В нүктесі қандай да бір қисық сызық сызады.
Кері айналдырылған қозғалыста Аi 1 Вi 1 Сi 1 нүктелердің лездік қалыптарын былайша салуға болады. Аi 1 нүктесі А нүктесін бұрышқа бүру арқылы анықталады. Сi 1 нүктесі сондай-ақ С нүктесін Е нүктесінің төңірегінде, бұрышқа бұру арқылы анықталады, оны ЕСі радиуспен Е нүктесінен жүргізген шенбер мен ДС радиуспен Д; нуктесінен жүргізілген шеңбердің қиылысқан жерінен табуға болады. Вi 1 нүктесін салу үшін Вi Сi радиуспен С' нүктесінен жүргізілген және АВ радиуспен Аi 1 нүктесінен жүргізілген екі доғаның қиылысқан нүктесін пайдаланамыз.
4. Кері айналдырылған козғалыста ЕД звеносы тоқтатылып қойылғандықтан есептің бүдан кейінгі шешімі қозғалмас звено ЕД аркылы бірнеше Вi 1 Сi 1 орындарымен берілген ВС звеносының жазықтығында айналма нүкте F пен G цеyтрін табуға тіреледі. Бұл мақсат үшін Бурместер геометриясын пайдаланамыз.
Табылған нүктелерді бірімен-бірін қосып, іздеп отырған АВСDЕFG механизмді табамыз.
Қолданылған әдебиеттер:
негізгі:
1. Қазақстан Республикасының үкімет қаулысы №918 19 тамыз 2002 ж. «Жобалау алды құжаттардың жеке түрлері, сонымен қатар жобалау (жобалау-сметалық) құжаттар бойынша сараптау жүргізу туралы ережелер»
2. Қазақстан Республикасының үкіметі 19 тамыз 2002 ж. №918 «Кейбір күш жоғалтқан Қазақстан Республикасының үкіметі шешімдерінің тізімі» қаулысына қосымша
3. Қазақстан Республикасының үкімет қаулысымен бекітілген 19 тамыз 2002 ж. №918 «Жобалау алды құжаттардың жеке түрлері, сонымен қатар жобалау (жобалау-сметалық) құжаттар бойынша сараптау жүргізу туралы ережелер»
4. ҚР ҚНжЕ А.2.2-1-2001 «Кәсіпорындар, ғимараттар және биналар құрылысына жобалық-сметалық құжаттарды өңдеу, бекіту және құрам реті туралы нұсқау». Астана, 2002.
қосымша:
1. ҚР ҚНжЕ 3.02-01«Тұрғын ғимараттар». Астана, 2002.
2. ҚР ҚНжЕ 3.02-02-2001 «Қоғамдық ғимараттар мен биналар». Астана, 2002.
3. СНиП 2.09.02-85* «Производственные здания». Москва, 1986.
Бақылау сұрақтары:
1.Механизмдердің синтезі үшін нені пайдаланған ықғайлы?
2. Төртінші кластық екінші ретті неден тұрады?
ДӘРІС 10
Тақырыбы: Жетектегі звеноның орташа жылдамдығының өзгеруінің берілген коэфиценті бойынша. қозғалыс заңдары
Мақсаты: Жетектегі звеноның орташа жылдамдығының өзгеру коэфиценті бойынша қозғалыс заңы.
Дәріс тезистері:
1. Жұдырықшалы механизмдер
2. Механизмдер жұмысының динамикалық шарттары
Жұдырықшалы механизмдер арқылы кез келген қозғалыс заңын теория жүзінде жүзеге асыруға болады, бірақ практикада профилі карапайым технологиялық методтармен өңделетін жұдырықшалы механизмнің кинематикалық және динамикалық шарттарын канағаттандыратын заңдарды қолданады.
Кинематикалық талаптар жүмыстың технологиялық шарттарымен анықталады, ал динамикалық талаптар динамикалық мүмкін күштермен анықталады.
Механизмдер жұмысының динамикалық шарттары үдеу аналогынық өзгеру заңына байланысты.
1.Қозғалыстың тең үдеттілген заңында механизмде A,B,C,D,E,F нүктелерінде жұмсақ соққылар болады.Бұл соққылар жетектегі звеноның кейбір соңғы шамадағы үдеулер өзгерісіне байланысты болады.
2. Екі қозғалыстың синусоидалы заңындағы жетектегі звеноның қозғалысы соққысыз болады
3. Косинусоидалы заңда жетектегі звеноның қозғаласы жетектегі звено жүрісінің басында және соңында жұмсақ соққылы болады.
4. Жетектегі звено қозғалысы сызықтық кемуші заңында жетктегі звено жүрісінің басында және соңында жұмсақ соққылы (A,C,D,F) болады.
5. Сызықтық өсуші заңда жетектегі звено қозғалысы оның орташа жүріс кезінде жұмсақ соққылы болады (В,Е). Мұнда үдеу лезде өз таңбасын өзгертеді.
6. Трапециалы заңда жетектегі звено қозғалысы соққысыз болады.
7. Жететемелі звено қозғалысының үдеуі тұрақты заңы. Егер жетектегі звено қозғалысының жылдамдығы тұрақты болса, онда жетектегі звено жүрісінің басында және соңында қатаң соққылар болуы мүмкін. Мұнда теориялық жағынан ұдеулер мен күштер мәні шексіздікке тең, ал практикалық жағынан өңдегендегі жұдырықшаның профилі дөңгелегі және материалдың серпімділігінің салдарынан үдеулер мен күштердің мәні шексіздікке тең болмайды.
Қолданылған әдебиеттер:
негізгі:
1.Технические и социально-экономические проблемы: эффективные пути их решения.: научная монография [под. ред. С.М. Ахметова]. Новосибирск: Изд. «СибАК». — 198 с.
2.Жакипбеков К.С.,Датхаев У.М., Жумабаев Н.Ж., Сакипова З.Б.Современное состояние привлечения инвестиций в фармацевтическую промышленность Республики Казахстан. Современная медицина: актуалные вопросы./Сб. Ст. по материалам XXVIII междунар. науч-практ. конф. № 2(28). Новосибирск: Изд. «СибАК», 2014. - С. 108-115.
Бақылау сұрақтары:
1. Механизмдер жұмысының динамикалық шарттары неге байланысты?
2. Кинематикалық талаптар қандай шарттармен анықталады?
