| a | b | c | |
| a | 0.5 | - | |
| b | 0.5 | ||
| c | - | 0.5 |
В данной матрице представлена следующая информация:
1. объекты a, b и c равноценны сами себе (по диагонали матрицы стоит 0.5),
2. объект a предпочтительнее объекта b,
3. объект b предпочтительнее c,
4. объекты a и с несравнимы.
В отличие от ранжирования, где должно выполняться условие о том, что, если а предпочтительнее b, а b предпочтительнее с, то а предпочтительнее с, попарное сравнение такого условия не предполагает. Попарное сравнение считается наиболее простым и надежным способом выявления предпочтений экспертов, потому что качественно сравнить объекты в парах, как правило, гораздо легче.
Множественное сравнение является развитием метода попарных сравнений, когда эксперту последовательно предлагают выбор из нескольких объектов, и в каждом выборе объекты надо упорядочить или указать лучший.
Непосредственное оценивание. Более сложным является попарное выражение предпочтений в числовом представлении. При этом эксперт может указать доли суммарной интенсивности для двух представленных объектов (суммарная интенсивность, как правило, устанавливается равной 1). Результаты экспертного оценивания в числовом выражении записывают в соответствующую матрицу.
Предположим, при сравнении трех вариантов развития предприятия a, b, c эксперт первой паре вариантов задает соотношение 0.6 и 0.4, для первого и третьего вариантов – 0.7 и 0.3, а для второго и третьего – 0.8 и 0.2. Матрица, отражающая результаты такого экcпертного оценивания будет иметь следующий вид:
| a | b | c | |
| a | 0.5 | 0.6 | 0.7 |
| b | 0.4 | 0.5 | 0.8 |
| c | 0.3 | 0.2 | 0.5 |
Перед экспертом также может быть поставлена задача указать, во сколько раз один элемент превосходит другой по важности. При этом задается балльная шкала предпочтений. Часто применяется семибальная шкала. При этом aij = 1, если элементы i и j равнопредпочтительны, aij = 3, если эксперт считает элемент i предпочтительнее j, aij=5, если у эксперта достаточно высокие основания считать элемент i предпочтительнее j, aij = 7, если у эксперта есть все основания считать элемент i предпочтительнее j.
Оценки эксперта записывают в матрицу. В этом случае по диагонали ставят 1 (элементы равноценны сами себе). Затем, начиная с первой строки матрицы, слева направо и сверху вниз последовательно записывают оценки соответствующей пары элементов, причем:
§ если элементы равнопредпочтительны, ставится 1,
§ если элемент текущей строки предпочтительнее элемента текущего столбца, то записывается соответствующая оценка (3, 5 и т.п.),
§ если элемент текущей строки уступает элементу текущего столбца, то оценка определяется по правилу  =
= 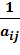
Возможны и другие варианты выставления оценок важности экспертами. Например, эксперта просят указать вероятность (в данном контексте ее называют субъективной) реализации определѐнного комплекса условий развития оцениваемых ситуаций с учетом некоторых неопределенных факторов, влияющих на развитие этих ситуаций (например, политических, социальных, инновационных, природных или других факторов).
Контрольные вопросы:
1. Назовите основные способы выражения предпочтений экспертов.
2. Что такое группировка?
3. В чем заключается бальное оценивание?
4. Что такое ранжирование и каким образом эта процедура позволяет оценить схожесть мнений экспертов?
5. Опишите возможности метода попарных сравнений. В каких методах он получил свое развитие?






