Любое экспертное решение может быть принято только на основе согласованных мнений экспертов. Поэтому подводя окончательные суждения, из экспертной группы исключают тех, чье мнение отличается от мнения большинства. При этом отсеиваются как неквалифицированные, так, возможно, и наиболее оригинальные мыслители, глубже большинства осознающие проблему. Если мнения разделились, то экспертов делят на две или более групп, имеющих сходные точки зрения внутри каждой группы.
Бывает, что вместо одной согласованной во мнениях, обнаруживаются две или несколько групп экспертов. В этом случае, либо изучается отдельно мнение каждой группы, либо считают, что опрос не достиг цели. Стремление обеспечить согласованность мнений экспертов в последнем случае может привести к одностороннему подбору экспертов, игнорированию всех возможных точек зрения.
Рассмотрим основные способы выражения предпочтений экспертов.
Начнем с качественных оценок, полученных в порядковых и номинальных шкалах. Работа с этими оценками позволяет: построить группировку, дать балльное оценивание, провести ранжирование, попарные и множественные сравнения.
Группировка (сортировка, классификация) состоит в том, что исследуемое множество разбивают на n классов и эксперт последовательно относит предлагаемые объекты к одному из классов. Внутри каждого класса объекты считаются равнопредпочтительными.
Балльное оценивание заключается в том, что каждому элементу исследуемого множества ставят в соответствие балл, заданный по заранее известным экспертам и неизменным правилам. Балльные оценки выбирают по специальной балльной шкале, имеющей определенное число делений. Чем больше число делений, тем на большее число классов разбивается множество, тем, с одной стороны, точнее, может оказаться оценка каждого объекта, а, с другой, тем сложнее экспертам оценить предпочтительность объекта.
В настоящее время распространены маркетинговые, социологические и иные опросы, в которых опрашиваемых просят выставить баллы объектам, изделиям, технологическим процессам, предприятиям, проектам, заявкам на выполнение научно-исследовательских работ, идеям, программам, политикам и т.п. Затем рассчитывают средние баллы и рассматривают их как обобщенные, итоговые оценки, выставленные коллективом опрошенных экспертов.
Ранжирование (упорядочение) – это представление объектов исследуемого множества в порядке убывания их предпочтительности с учетом какого-то одного или нескольких свойств, при этом допускается указание на равноценность объектов.
Как уже было отмечено, получаемые от экспертов мнения часто выражены в порядковой шкале, т.е. эксперт может сказать (и обосновать), что один тип продукции будет более привлекателен для потребителей, чем другой, один показатель качества продукции более важен, чем другой. Но он не в состоянии сказать, во сколько раз или на колько более важна одна характеристика по отношению к другой. Поэтому экспертов часто просят упорядочить объекты экспертизы в порядке возрастания (неубывания) интенсивности интересующей организаторов экспертизы характеристики. Ранг - это номер объекта экспертизы в упорядоченном ряду.
Формально ранги выражаются числами 1, 2, 3,..., но важно отметить, что с этими числами нельзя делать привычные арифметические операции. Например, хотя 2 + 3 = 5, но нельзя утверждать, что для объекта, стоящего на третьем месте в упорядочении (в другой терминологии - ранжировке), интенсивность изучаемой характеристики равна сумме интенсивностей объектов с рангами 1 и 2 (знания отличника не равны сумме знаний двоечника и троечника, хотя 5 = 2 + 3). Поэтому для анализа подобного рода качественных данных необходима не обычная арифметика, а другая теория, дающая базу для разработки, изучения и применения конкретных методов расчета.
Заметим, что оценить схожесть мнений экспертов в данном случае можно визуальным анализом, если исходную таблицу рангов объектов представить в виде другой таблицы, в которой столбцы переставлены таким образом, чтобы ранги, данные первым экспертом, располагались в порядке возрастания.
Предположим, исходная таблица рангов семи инвестиционных проектов имеет вид:
| x¹ | x² | x³ | 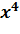
| 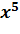
| 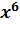
| 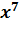
| |
| Эксперт 1 | |||||||
| Эксперт 2 |
После перестановки столбцов в соответствии с возрастанием рангов, данным первым экспертом, получим следующую таблицу:
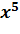
| 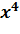
| x² | x¹ | 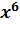
| x³ | 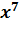
| |
| Эксперт 1 | |||||||
| Эксперт 2 |
Анализ таблицы показывает, что мнения экспертов достаточно близки. Обычно ранги присваиваются в порядке убывания привлекательности проекта, т.е. наиболее привлекательному варианту присваивается значение 1 и по мере уменьшения привлекательности они возрастают. Из таблицы видно, что оценки, данные лучшим проектам обоими экспертами, (x5 и x4) совпадают. В остальных случаях, хотя оценки и не совпадают, различие между ними в основном не превышает 1, лишь для 6-го проекта эта разница равна 2. В большинстве случаев совпадают направления ранжировки инвестиционных проектов, от меньшего значения ранга к большему: от 4-го ко 2-му, от 1-го к 6-му, от 3-его к 7-му, от 5-го ко 2-му, от 5-го к 1-му, от 5-го к 6-му, от 5-го к 3-му и т.д.
Не совпадают непосредственно оценки 1-го, 6-го, 3-го и 7-го объектов и порядок ранжировки от 2-го к 1-му, от 1-го к 6-му, от 6-го к 3-му и от 3-го к 7-му и от 6-го к 7-му. Однако, учитывая, что наибольшая несогласованность касается проектов, получивших низкие оценки предпочтительности, можно сказать, что этот разброс мнений не столь важен.
Попарное сравнение состоит в указании более предпочтительного объекта в паре объектов или их равноценности. Результаты попарного сравнения удобно представить в виде матрицы. На пересечении строки i и столбца j ставится 1, если объект i предпочтительнее объекта j, 0 - если объект j предпочтительнее объекта i, и ½ - если объекты равноценны и прочерк (—), если объекты несравнимы.






