a) -2cos х = 1; б) cos 2х - 1 = 0;
в) 2cos 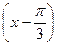 =
=  ; г)
; г) 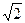 - 2cos
- 2cos  = 0.
= 0.
Очікувана відповідь: а) ±  +2πn, n
+2πn, n  Z; б) π n, n
Z; б) π n, n  Z;
Z;
в) 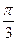 ±
±  +π n, n
+π n, n  Z; r)
Z; r) 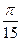 ±
± 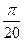 +
+  , n
, n  Z.
Z.
Повернемось до вирішення нашої проблеми: На початку заняття ми не вміли розв’язати рівняння: 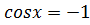 ,
, 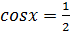
Як бачимо, це найпростіші тригонометричні рівняння відносно косинуса, обидва мають розв’язки: 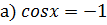 , x = π + 2πп, п
, x = π + 2πп, п  Z, як окремий випадок; б)
Z, як окремий випадок; б) 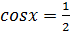 , x =
, x = 
 + 2πп, п
+ 2πп, п  Z, за загальним розв’язком.
Z, за загальним розв’язком.
4.2. Розв'язування найпростішого тригонометричного рівняння sin x = a.

1. Якщо | а | > 1, то рівняння не має розв'язків, поскільки | sin x |  1 для будь-якого x.
1 для будь-якого x.
2. Якщо | а | < 1, то, враховуючи те, що sin x — ордината точки Рx одиничного кола, маємо: ординату, рівну а, мають дві точки одиничного кола (на осі OY відкладаємо число а і через цю точку проведемо пряму, перпендикулярну до осі ординат (рис. 123), яка перетне коло у двох токах -  і
і 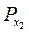 ):
):
x 1 = arcsin a + 2πп, п  Z,
Z,
x 2 = π - arcsin а + 2πп, п  Z.
Z.
Ці дві формули можна записати у вигляді однієї формули:
x = (-1) k arcsin a + πk, k  Z Z
| (1) |
Неважко впевнитися, що при парному k = 2п маємо:
x 1 = (-1)2 n arcsin а + 2π п або x 1 = arcsin a + 2πп, п  Z;
Z;
при непарному k = 2 n + 1 маємо:
x 2 = (-1)2 n +1 arcsin а + (2 n + 1)π;
x 2 = - arcsin а + 2πп + π;
x 2 = π - arcsin a + 2πп, п  Z.
Z.
Окремі випадки.
· Якщо а = 1, то, враховуючи те, що sin t — це ордината точки Pt(одиничного кола, маємо: ординату, рівну 1, має точка Рt утворена із точки Р 0(1;0) поворотом на кут  + 2πп, п
+ 2πп, п  Z.
Z.
Отже, t =  + 2πп, п
+ 2πп, п  Z.
Z.
· Якщо а = -1, то t = -  + 2πп, п
+ 2πп, п  Z. "
Z. "
· Якщо а = 0, маємо t = 0 + π п; t =πп, п  Z.
Z.
Розглянемо приклади.
Приклад 1. Розв'яжіть рівняння sinx = 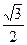 .
.
Розв'язання
Згідно з формулою (1) маємо: х = (-1) n arcsin 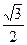 + π п, п
+ π п, п  Z.
Z.
Оскільки arcsin 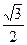 =
=  , то х = (-1) n
, то х = (-1) n  + π n, п
+ π n, п  є Z.
є Z.
Очікувана відповідь: (-1) n  + π n, п
+ π n, п  є Z.
є Z.
Приклад 2. Розв'яжіть рівняння sin х = -  .
.
Розв'язання
Згідно з формулою (1) маємо: х = (-1) n arcsin  + π п, п
+ π п, п  Z.
Z.
Оскільки arcsin  = -
= -  , то х = (-1) n ·
, то х = (-1) n · 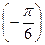 + π n, n
+ π n, n  Z; х = (-1) n +1 + π п, п
Z; х = (-1) n +1 + π п, п  Z.
Z.
Очікувана відповідь: (-1) n +1 + π п, п  Z.
Z.
Приклад 3. Розв'яжіть рівняння sin x =  .
.
Розв'язання
Оскільки  , то згідно з формулою (1) маємо: х = (-1) n arcsin
, то згідно з формулою (1) маємо: х = (-1) n arcsin 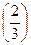 + π п, п
+ π п, п  Z.
Z.
Очікувана відповідь: (-1) n arcsin 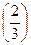 + π п, п
+ π п, п  Z.
Z.
Коментоване виконання вправ під керівництвом викладача (закріплення знань, формування вмінь і навичок, метод – навчальний тренажер)
Розв’язати найпростіші тригонометричні рівняння
a) 2sin х - 1 = 0; б) 2sin 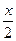 = - l;
= - l;
в) 2sin  = -
= - 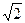 ; г) 2sin
; г) 2sin 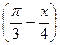 =
=  .
.
Очікувані відповіді: а) (-1) n 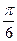 + π n, n
+ π n, n  Z; б) (-1) n+ 1
Z; б) (-1) n+ 1  + 2πп, п
+ 2πп, п  Z;
Z;
в) 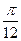 +(-1) n +1
+(-1) n +1 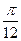 +
+ 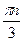 , п
, п  Z; г)
Z; г) 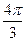 +(-l) n +1
+(-l) n +1 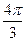 +4π n, п
+4π n, п  Z
Z
4.4. Розв'язування найпростішого тригонометричного рівняння tg x = a (ctg x = a).

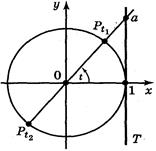 Розв'язування рівняння tg x = а зручно проілюструвати за допомогою лінії тангенсів (рис. 1). tg x — це ордината точки перетину прямої ОРx з лінією тангенсів. Відкладемо на осі тангенсів число а, через цю точку і початок координат проведемо пряму, яка перетне одиничне коло у двох точках
Розв'язування рівняння tg x = а зручно проілюструвати за допомогою лінії тангенсів (рис. 1). tg x — це ордината точки перетину прямої ОРx з лінією тангенсів. Відкладемо на осі тангенсів число а, через цю точку і початок координат проведемо пряму, яка перетне одиничне коло у двох точках  і
і  , тоді
, тоді
x = arctg а + π n, n  Z Z
| (1) |
Отже, рівняння tg x = а при будь-якому значенні а має розв'язок.
Рівняння ctg x = а, де а ≠ 0 рівносильне рівнянню tg x =  .
.
Проте можна довести, що розв'язки рівняння ctg x = а можна записати у вигляді: x = arcctg a + π п, n  Z
Z
Розглянемо приклади.
Приклад 1. Розв'яжіть рівняння tg x =  .
.
Розв'язання
По формулі (1) знаходимо х = arctg  + π п, п
+ π п, п  Z.
Z.
Оскільки arctg  =
=  , то маємо: х =
, то маємо: х =  + π п, п
+ π п, п  Z.
Z.
Очікувана відповідь:  + π п, п
+ π п, п  Z.
Z.
Приклад 2. Розв'яжіть рівняння tg х = 2.
Розв'язання
За формулою (1) маємо: х = arctg 2 + π п, п  Z.
Z.
Очікувана відповідь: arctg 2 + π п 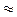 1,1 + π п, п
1,1 + π п, п  Z.
Z.
Приклад 3. Розв'яжіть рівняння ctg x –  = 0.
= 0.
Розв'язання
ctg х –  = 0; ctg х =
= 0; ctg х =  ; tg х =
; tg х =  , x = arctg
, x = arctg  + πп =
+ πп =  + π n, n
+ π n, n  Z.
Z.
Очікувана відповідь:  + π n, n
+ π n, n  Z.
Z.
5. Узагальнення та систематизація знань, умінь та навичок студентів. (бесіда,самостійна робота за індивідуальними варіантами з вибірковим контролем)
Як бачимо, при розв’язуванні найпростіших тригонометричних рівнянь необхідно виконати наступний алгоритм:
1. Визначити тип рівняння. (cosx = а, sinx = а, tgx = а чи ctgx = а).
2. Якщо це один із двох перших типів, то з’ясувати загальний чи окремий випадок.
3. Застосувати відповідну формулу.
Студентам пропонується самостійна робота за індивідуальними варіантами з вибірковим контролем по виконанню
6.Підведення підсумків заняття .(рефлексія)
Студентам пропонується дати відповідь на питання:
1. Як ви оцінюєте власну роботу на занятті?
2. Як ви оцінюєте роботу групи?
3. Де ви використаєте набуті знання?
4. Чи стануть вам у пригоді здобуті знання та вміння в майбутній професійній діяльності?
Викладач підводить підсумки заняття, відмічає роботу студентів, коментує отримані оцінки на занятті відповідно до складеної рейтингової таблиці.
7. Домашнє завдання. Вивчити конспект.






