Хід заняття
1. Організаційна частина. (метод - психолого – педагогічної підтримки роботи студентів на занятті) 2 хв.
Викладач з’ясовує присутність студентів на занятті, налаштовує їх на роботу, відповідає на питання студентів щодо домашнього завдання, встановлює психолого – педагогічний контакт з групою.
Викладач роз’яснює зміст роботи на занятті, розповідає про спосіб оцінки знань, умінь та навичок за допомогою рейтингової таблиці, в якій будуть відображені всі види роботи на занятті.
2. Перевірка домашнього завдання. (метод – навчальний тренажер) 5 хв
1. Студенти- чергові перевіряють наявність домашніх завдань своїх колег, роблять відмітки в рейтинговій таблиці.
2. На екрані висвітлено вправи домашнього завдання з помилками. Студентам необхідно виявити їх та виправити, аргументуючи свої кроки.
3. Підготовка до заняття. (метод – навчальний інструктаж).
Оголошується тема, мета та завдання заняття.
Тема заняття: Найпростіші тригонометричні рівняння
3.2. План заняття.
3.2.1. Найпростіше тригонометричне рівняння cos t = a. Тренувальні вправи.
3.2.2. Найпростіше тригонометричне рівняння sin t = a. Тренувальні вправи.
3.2.3. Найпростіші тригонометричні рівняння tg t = a, ctg t = a. Тренувальні вправи.
3.2.4. Розв’язування різних типів найпростіших тригонометричних рівнянь.
Мотивація пізнавальної діяльності студентів.
1. (метод – проблемної бесіди).
Усім відомо, що квадратні рівняння можна розв'язувати за допомогою формули їх коренів, що значно спрощує роботу. Ми вже познайомились з різними типами квадратних рівнянь, які можна віднести до функціональних рівнянь (квадратні показникові, ірраціональні та квадратні логарифмічні рівняння). Як відомо вони розв’язуються за допомогою підстановки і зводяться до звичайного квадратного рівняння, для якого давно виведені формули коренів, але в процесі знаходження коренів необхідно через підстановку повернутись до старої змінної. Так спробуємо розв’язати також квадратне рівняння: 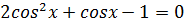
Проведемо заміну 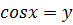 , тоді
, тоді 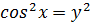 . Матимемо рівняння
. Матимемо рівняння
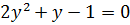
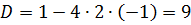 ,
, 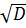 =3, тоді
=3, тоді
y1=  ; y2=
; y2= 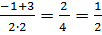 .
.
Отже, при повернені до старої змінної маємо рівняння виду:
 ,
, 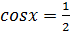 . Таке рівняння ми розв’язувати поки не вміємо. Розв’язуванню рівняння такого виду і присвячується наше занняття
. Таке рівняння ми розв’язувати поки не вміємо. Розв’язуванню рівняння такого виду і присвячується наше занняття
 У математиці розглядають рівняння, у яких невідоме (змінна) входить тільки під знак тригонометричних функцій, наприклад:cos t = 1, cos t + sin t = 0. Ці рівняння називаються тригонометричними рівняннями. На наступних заняттях ми будемо вивчати різні типи тригонометричних рівнянь, що будуть зводитись до відомих алгебраїчних рівнянь. Але, як правило, розв'язування будь-якого тригонометричного рівняння рано чи пізно зводиться до розв'язування найпростіших рівнянь: sin t = a, cos t = a, tg t = a, ctg t = a, яким присвячується наше заняття.
У математиці розглядають рівняння, у яких невідоме (змінна) входить тільки під знак тригонометричних функцій, наприклад:cos t = 1, cos t + sin t = 0. Ці рівняння називаються тригонометричними рівняннями. На наступних заняттях ми будемо вивчати різні типи тригонометричних рівнянь, що будуть зводитись до відомих алгебраїчних рівнянь. Але, як правило, розв'язування будь-якого тригонометричного рівняння рано чи пізно зводиться до розв'язування найпростіших рівнянь: sin t = a, cos t = a, tg t = a, ctg t = a, яким присвячується наше заняття.
Отже, наше завдання — вивести формули для розв'язування найпростіших тригонометричних рівнянь та навчитись розв’язувати різні типи найпростіших тригонометричних рівнянь.
3.4. Актуалізація опорних знань студентів. (фронтальна бесіда- бліц - опитування, математичний диктант, метод:контролю і взаємоконтролю самостійної роботи студентів)
1.Усне бліц- опитування.
· Яка функція називається оборотною?
· Необхідна умова оборотності функції.
· Достатня умова оборотності функції.
· Чи задовольняють умови оборотності тригонометричні функції  для довільних значень змінної x?
для довільних значень змінної x?
· Як ми вирішуємо цю проблему?
· Що називається арксинусом числа a?
· Що таке арккосинус числа a? Чому дорівнює арккосинус від’ємного аргументу?
· Що таке арктангенс числа a?
· Що таке арккотангенс числа a? Чому дорівнює арккотангенс від’ємного аргументу?
2.Математичний диктант
Варіант -1Варіант -2
1) arcsin 1; 1) arccos  ;
;
2) arcsin  ; 2) arccos
; 2) arccos  ;
;
3) arcsin 0; 3) arсcos (-l);
4) arccos 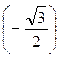 ; 4) arccos
; 4) arccos  ;
;
5) arcsin  ; 5) arctg
; 5) arctg  ;
;
6) arcctg 1; 6) arctg 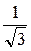 ;
;
7) arсtg 0; 7) arcctg 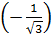 ;
;
8) arcctg(-  ); 8) arctg1
); 8) arctg1
Очікувані відповіді:
В-1 1) 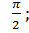 2)
2) 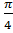 ; 3) 0; 4)
; 3) 0; 4)  ; 5) -
; 5) -  ; 6)
; 6)  ; 7) 0; 8)
; 7) 0; 8) 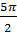 .
.
В-2 1) 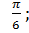 2)
2)  ; 3)
; 3)  ; 4)
; 4)  ; 5) -
; 5) -  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  .
.
Студенти в парах міняються виконаними завданнями та за наведеними відповідями перевіряють один одного виставляючи бали, що відповідають кількості вірних завдань.
4. Вивчення нового матеріалу .(методи – пояснювально – ілюстративний, навчальний тренажер, опора на життєвий досвід).
4.1. Найпростіше тригонометричне рівняння cosx = а.
1. Якщо | а | > 1, то рівняння cos x = а не має розв'язків, по-скільки |cos x | < 1 для будь-якого x.
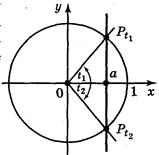
2. Якщо | а | < 1, то враховуючи те, що cos x — абсциса точки Рx одиничного кола, маємо: абсцису, рівну а, мають дві точки (рис. 122) одиничного кола(на осі ОХ відкладемо число а і через побудовану точку проведемо пряму, перпендикулярну до осі абсцис, яка перетне коло у двох точках 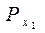 і
і 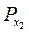 . Тоді
. Тоді
x 1 = arccos a + 2πп, п  Z,
Z,
x 2 = - arccos а + 2πп, п  Z.
Z.
Ці розв'язки можна об'єднати x = ± arccos a + 2πп, n  Z
Z

Окремі випадки
· Якщо а = 1, то, враховуючи те, що cos x — це абсциса точки Рt одиничного кола, маємо: абсцису, рівну 1, має точка Рt утворена із точки Р0 (1; 0) поворотом на кути 2πп, п  Z. Отже, x = 0 + 2πп = 2πп, п
Z. Отже, x = 0 + 2πп = 2πп, п  Z
Z
· Якщо а = -1, то маємо x = π + 2πп, п  Z.
Z.
· Якщо а = 0, то маємо x =  + πп, п
+ πп, п  Z.
Z.
Корені рівнянь: cos x = 1, cos x = -1, cos x = 0 також можна одержати із формули x = ± arccos a + 2πп, п  Z. Розглянемо приклади.
Z. Розглянемо приклади.
Приклад 1. Розв'яжіть рівняння cos x = 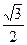 .
.
Розв'язання
Згідно з формулою (1) маємо:
х = ± arccos 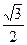 + 2πn, п
+ 2πn, п  Z.
Z.
Оскільки arccos 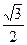 =
=  , то маємо: х = ±
, то маємо: х = ±  + 2π п, п є Z.
+ 2π п, п є Z.
Очікувана відповідь: ±  + 2π п, п
+ 2π п, п  Z.
Z.
Приклад 2. Розв'яжіть рівняння cos x = 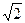 .
.
Розв'язання
Оскільки 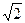 > 1, то рівняння коренів не має.
> 1, то рівняння коренів не має.
Очікувана відповідь: коренів немає.
Приклад 3. Розв'яжіть рівняння cos x = -  .
.
Розв'язання
Згідно з формулою (1) маємо: х = ±arccos  + 2πп, п
+ 2πп, п  Z.
Z.
Оскільки arccos  = π - arccos
= π - arccos  = π -
= π - 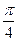 =
= 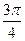 , то
, то
x = ± 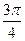 + 2π n, n
+ 2π n, n  Z.
Z.
Очікувана відповідь: ± 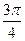 + 2π n, n
+ 2π n, n  Z.
Z.
Приклад 4. Розв'яжіть рівняння cos x = 0.
Розв'язання
Дане рівняння задовольняє вигляд окремого випадку тригонометричного рівняння. Тому його розв’язком буде x=  + π п, п
+ π п, п  Z.
Z.
Очікувана відповідь:  + π п, п
+ π п, п  Z.
Z.
Коментоване виконання вправ під керівництвом викладача. (закріплення знань, формування вмінь і навичок, метод – навчальний тренажер)






