Учебные материалы для выполнения

КОНТРОЛЬНОЙ РАБОТЫ № 2

Основные формулы

· Закон Кулона

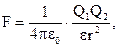
где F – сила взаимодействия двух точечных зарядов Q₁ и Q₂; r – расстояние между зарядами; e - диэлектрическая проницаемость среды; e₀ – диэлектрическая постоянная:

· Закон сохранения заряда

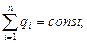
где - алгебраическая сумма зарядов, входящих в изолированную систему; n – число зарядов.

 

• Напряженность электрического поля

Е = F/q,

где F — сила, действующая на точечный положительный заряд q, помещенный в данную точку поля.

• Поток вектора напряженности Е электрического поля:

а) через произвольную поверхность S, помещенную в неодно­родное поле,

где а — угол между вектором напряженности Е и нормалью п к элементу поверхности; dS — площадь элемента поверхности; Еп — проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное элек­трическое поле,

Ф_Е=EScosa.

• Поток вектора напряженности Е через замкнутую поверхность

где интегрирование ведется по всей поверхности.

• Теорема Остроградского — Гаусса. Поток вектора напря­женности Е через любую замкнутую поверхность, охватывающую заряды q₁, q₂,…, q_n,

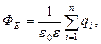
где — алгебраическая сумма зарядов, заключенных внутри

замкнутой поверхности; п — число зарядов.

• Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда,

• Напряженность электрического поля, создаваемого металли­ческой сферой радиусом R, несущей заряд q, на расстоянии r отцентра сферы:

а) внутри сферы (г < R)

Е=0;

б) на поверхности сферы (г = R)

в) вне сферы (г > R)

• Принцип суперпозиции (наложения) электрических полей, со­гласно которому напряженность Е результирующего поля, создан­ного двумя (и более) точечными зарядами, равна векторной (гео­метрической) сумме напряженностей складываемых полей:

Е= Е₁+Е₂+…+ Е_п.

В случае двух электрических полей с напряженностями Е₁ и Е₂ модуль вектора напряженности

где а — угол между векторами Е₁ и Е₂.

• Напряженность поля, создаваемого бесконечно длинной рав­номерно заряженной нитью (или цилиндром) на расстоянии r от ее оси,

где t — линейная плотность заряда.

Линейная плотность заряда есть величина, равная отношению заряда, распределенного по нити, к длине нити (цилиндра):

• Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,

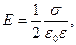
где s — поверхностная плотность заряда.

Поверхностная плотность заряда есть величина, равная отно­шению заряда, распределенного по поверхности, к площади этой поверхности:

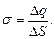
• Напряженность поля, создаваемого двумя параллельными бес­конечными равномерно и разноименно заряженными плоскостями с одинаковой по модулю поверхностной плотностью s заряда (поле плоского конденсатора)

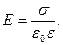
Приведенная формула справедлива для вычисления напряжен­ности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.

• Электрическое смещение D связано с напряженностью Е элек­трического поля соотношением

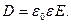
Это соотношение справедливо только для изотропных диэлек­триков.

• Циркуляция вектора напряженности электрического поля есть величина, численно равная работе по перемещению единичного положительного точечного заряда вдоль замкнутого контура. Циркуляция выражается интегралом по замкнутому контуру где 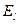— проекция вектора напряженности Е в данной точке контура на направление касательной к контуру в той же точке.

В случае электростатического поля циркуляция вектора напря­женности равна нулю:

• Потенциал электрического поля - величина равная отно­шению потенциальной энергии точечного положительного заряда, помещенную в данную точку поля, к этому заряду:

j= П/q,

1. или потенциал электрического поля есть величина, равная отноше­нию работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду:

j = A/q.

2. Потенциал электрического поля в бесконечности условно принят равным нулю.

Отметим, что при перемещении заряда в электрическом поле работа А_ВС внешних сил равна по модулю работе А_СП сил поля и противоположна ей по знаку:

А_ВС= - А_СП.

• Потенциал электрического поля, создаваемый точечным заря­дом q на расстоянии г от заряда,

• Потенциал электрического поля, создаваемого металлической, несущей заряд q сферой радиусом R, на расстоянии r от центра сферы:

внутри сферы (r < R) ;

на поверхности сферы (r = R) ;

вне сферы (r > R)

Во всех приведенных для потенциала заряженной сферы фор­мулах e есть диэлектрическая проницаемость однородного безгра­ничного диэлектрика, окружающего сферу.

• Потенциал электрического поля, созданного системой точеч­ных зарядов, в данной точке в соответствии с принципом суперпо­зиции электрических полей равен алгебраической сумме потенциа­лов j₁, j₂,…, j_n, создаваемых отдельными точечными зарядами q₁, q₂,…, q_n:

• Энергия W взаимодействия системы точечных зарядов q₁, q₂,…, q_n определяется работой, которую эта система зарядов может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой

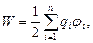
где j_i — потенциал поля, создаваемого всеми n - 1 зарядами (за исключением i-го) в точке, где расположен заряд q_i.

• Потенциал связан с напряженностью электрического поля со­отношением

Е = - gradj.

В случае электрического поля, обладающего сферической сим­метрией, эта связь выражается формулой

или в скалярной форме

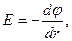
а в случае однородного поля, т.е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению,

E = (j₁ - j₂)/d,

где j₁ и j₂ — потенциалы точек двух эквипотенциальных по­верхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.

• Работа, совершаемая электрическим полем при перемещении точечного заряда Q из одной точки поля, имеющей потенциал j₁, в другую, имеющую потенциал j₂,

или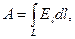

где E_l — проекция вектора напряженности Е на направление перемещения; dl — перемещение.

В случае однородного поля последняя формула принимает вид

А = qE^.l cos a,

где l— перемещение; a — угол между направлениями вектора Е и перемещения l.

• Электрическая емкость уединенного проводника или конден­сатора

С =D q / D j

где D q — заряд, сообщенный проводнику (конденсатору); Dj — изменение потенциала, вызванное этим зарядом.

• Электрическая емкость уединенной проводящей сферы ра­диусом R, находящейся в бесконечной среде с диэлектрической проницаемостью e,

Если сфера полая и заполнена диэлектриком, то электроемкость ее от этого не изменяется.

• Электрическая емкость плоского конденсатора

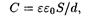
где S — площадь пластин (каждой пластины); d — расстояние между ними; e — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электрическая емкость плоского конденсатора, заполненного п слоями диэлектриком толщиной d_i каждый с диэлектрическими проницаемостями e_i (слоистый конденсатор),

• Электрическая емкость сферического конденсатора (две кон­центрические сферы радиусами R₁ и R₂, пространство между ко­торыми заполнено диэлектриком с диэлектрической проницаемо­стью e)

• Электрическая емкость цилиндрического конденсатора (два коаксиальных цилиндра длиной l и радиусами R₁ и R ₂, простран­ство между которыми заполнено диэлектриком с диэлектрической проницаемостью e)

• Электрическая емкость С последовательно соединенных конденсаторов:

в общем случае

 

где n — число конденсаторов;

в случае двух конденсаторов

в случае n одинаковых конденсаторов с электроемкостью С₁ каждый

 

• Электрическая емкость параллельно соединенных конденсато­ров:

в общем случае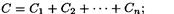

в случае двух конденсаторов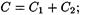

в случае та одинаковых конденсаторов с электроемкостью С₁ каждый С = пС₁.

• Энергия заряженного проводника выражается через заряд Q, потенциал j и электрическую емкость С проводника следующими соотношениями:

• Энергия заряженного конденсатора

где С — электрическая емкость конденсатора; U — разность потенциалов на его пластинах.

• Объемная плотность энергии (энергия электрического поля, приходящаяся на единицу объема)

где Е— напряженность электрического поля в среде с диэлек­трической проницаемостью e; D— электрическое смещение.

• Сила постоянного тока

где Q — количество электричества, прошедшее через поперечное сечение проводника за время t.

• Плотность электрического тока есть векторная величина, рав­ная отношению силы тока к площади S поперечного сечения про­водника:

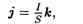
где k — единичный вектор, по направлению совпадающий с на­правлением движения положительных носителей заряда.

• Сопротивление однородного проводника

где r — удельное сопротивление вещества проводника; l — его длина.

• Проводимость G проводника и удельная проводимость g ве­щества

• Зависимость удельного сопротивления от температуры

где r и r₀ — удельные сопротивления соответственно при t и 0°С; t — температура (по шкале Цельсия); a — температурный коэффициент сопротивления.

• Сопротивление соединения проводников:

последовательного

параллельного

Здесь R_i — сопротивление i-го проводника: п — число провод­ников.

• Закон Ома:

для неоднородного участка цепи

для однородного участка цепи

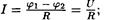
для замкнутой цепи (j₁=j₂) I = e /R

Здесь (j₁ - j₂) — разность потенциалов на концах участка цепи; e₁₂ — ЭДС источников тока, входящих в участок; U — напряжение на участке цепи; R — сопротивление цепи (участка цепи.

• Правила Кирхгофа. Первое правило: алгебраическая сумма сил токов, сходящихся в узле, равна нулю, т. е.

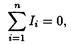
где n — число токов, сходящихся в узле.

Второе правило: в замкнутом контуре алгебраическая сумма напряжений на всех участках контура равна алгебраической сумме электродвижущих сил, т. е.

где I_i — сила тока на i-м участке; R_i — активное сопротивление на i-м участке; ξ _i — ЭДС источников тока на i-м участке; п — число участков, содержащих активное сопротивление; k — число участков, содержащих источники тока.

• Работа, совершаемая электростатическим полем и сторонними силами в участке цепи постоянного тока за время t,

• Мощность тока

• Закон Джоуля — Ленца

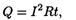
где Q — количество теплоты, выделяющееся в участке цепизавремя t.

Закон Джоуля — Ленца справедлив при условии, что участок цепи неподвижен и в нем не совершаются химические превращения.

ЭЛЕКТРОМАГНЕТИЗМ

Основные формулы

• Закон Био — Савара — Лапласа

где dB — магнитная индукция поля, создаваемого элементом про­водника с током; m — магнитная проницаемость; m₀ = 4p×10^-7 Гн/м — магнитная постоянная; d l — вектор, равный по моду­лю длине dl проводника и совпадающий по направлению с током (элемент проводника); I — сила тока; r — радиус-вектор, про­веденный от середины элемента проводника к точке, магнитная индукция в которой определяется.

Модуль вектора dB выражается формулой

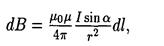
где a — угол между векторами d l и r.

• Магнитная индукция В связана с напряженностью Н магнит­ного поля (в случае однородной, изотропной среды) соотношением

или в вакууме

• Магнитная индукция в центре кругового проводника с током

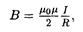
где R — радиус кривизны проводника.

• Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,

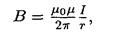
где r — расстояние от оси проводника.

Магнитная индукция поля, создаваемого отрезком проводника,

 

При симметричном расположении концов проводника относительно точки, в которой определяется магнитная ин­дукция, -cosj₂ = cosj₁ = cosj и, следовательно,

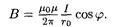
• Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси),

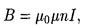
где n — число витков, приходящихся на единицу длины соленоида; I — сила тока в одном витке.

• Принцип суперпозиции магнитных полей: магнитная индук­ция В результирующего поля равна векторной сумме магнитных индукций B₁, B ₂,…, В_п складываемых полей, т. е.

В частном случае наложения двух полей

а модуль магнитной продукции

где a — угол между векторами В₁ и В₂.

• Закон Ампера. Сила, действующая на проводник с током в магнитном поле,

где I — сила тока; I — вектор, равный по модулю длине I про­водника и совпадающий по направлению с током; В — магнитная индукция поля.

Модуль вектора F определяется выражением

где а — угол между векторами I и В.

• Сила взаимодействия двух прямых бесконечно длинных парал­лельных проводников с токами I₁ ц 1₂, находящихся на расстоянии d друг от друга, рассчитанная на отрезок проводника длиной I, выражается формулой

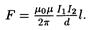
• Магнитный момент контура с током

где S — вектор, равный по модулю площади S, охватываемой контуром, и совпадающий по направлению с нормалью к его плоскости.

• Механический момент, действующий на контур с током, по­мещенный в однородное магнитное поле,

Модуль механического момента

где a — угол между векторами р_т и В.

• Потенциальная (механическая) энергия контура с током в магнитном поле

• Сила, действующая на контур с током в магнитном полe, изменяющемся вдоль оси x,;

где — изменение магнитной индукции вдоль оси Ох, расcчитанное на единицу длины; а — угол между векторами р_т и B.

• Сила F, действующая на заряд Q, движущийся со скоростью v в магнитном поле с индукцией В (сила Лоренца), выражается формулой

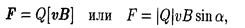
где a — угол, образованный вектором скорости v движущейся частицы и вектором магнитной индукции В.

• Работа по перемещению замкнутого контура с током в маг­нитном поле

А =I DФ,

где DФ — изменение магнитного потока, пронизывающего поверх­ность, ограниченную контуром; I — сила тока в контуре.

• Основной закон электромагнитной индукции (закон Фарадея— Максвелла)

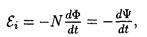
где e _i — электродвижущая сила индукции; N — число витков контура; y— потокосцепление.

Частные случаи применения основного закона электромагнитной индукции:

а) разность потенциалов U на концах проводника длиной l, движущегося со скоростью v в однородном магнитном поле,

где a — угол между направлениями векторов скорости v и маг­нитной индукции В;

б) электродвижущая сила индукции ξ_i, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью w в однородном магнитном поле с индукцией В

где wt — мгновенное значение угла между вектором В и вектором нормали п к плоскости рамки.

• Количество электричества Q, протекающего в контуре,

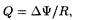
где R — сопротивление контура; Dy — изменение потокосцепления.

• Электродвижущая сила самоиндукции ξ_i, возникающая в зам­кнутом контуре при изменении силы тока в нем,

где L — индуктивность контура.

 

• Потокосцепление контура

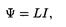
где L — индуктивность контура.

• Индуктивность соленоида (тороида)

Во всех случаях вычисления индуктивности соленоида (тороида) с сердечником по приведенной формуле для определения магнитной проницаемости следует пользоваться графиком зависимости В от Н (см. рис. 24.1), а затем формулой

• Мгновенное значение силы тока I в цепи, обладающей актив­ным сопротивлением R и индуктивностью L:

а) после замыкания цепи

где Е — ЭДС источника тока; t — время, прошедшее после замыкания цепи;

б) после размыкания цепи

где I₀ — сила тока в цепи при t = 0; t — время, прошедшее с момента размыкания цепи.

• Энергия W магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, определяется формулой

где I — сила тока в контуре.

• Объемная (пространственная) плотность энергии однородного магнитного поля (например, поля длинного соленоида)

 

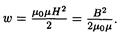
Примеры решения задач

Пример 1. Тонкий стержень длиной l = 30 см несёт равномерно распределённый по длине заряд с линейной плотностью t = 1 мкКл/м. На расстоянии r₀ = 20 см от стержня находится заряд Q₁ = 10 нКл, равноудаленный от концов стержня. Определить силу F взаимодействия точечного заряда с заряженным стержнем.

Решение. Закон Кулона позволяет вычислить силу взаимодействия точечных зарядов. По условию задачи, один из зарядов не является точечным, а представляет собой заряд, равномерно распределённый по длине стержня. Однако если выделить на стержне малый участок длиной dl, то находящийся на нём заряд d Q = tdl можно рассматривать как точечный и тогда по закону Кулона сила взаимодействия между зарядами Q₁ и d Q:

(1)

где r – расстояние от выделенного элемента до заряда Q₁.

Из чертежа следует, что и , где r₀ – расстояние от заряда Q₁до стержня. Подставив эти выражения r и dl в формулу (1), получим

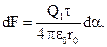(2)

Следует иметь в виду, что d F – вектор, поэтому, прежде чем интегрировать, разложим его на две составляющие: d F₁, перпендикулярную стержню, и d F₂, параллельную ему.

Из рисунка видно, что dF₁ = dF×cosa, dF₂ = dF×sina. Подставляя значение dF из выражения (2) в эти формулы, найдём:

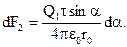
Интегрируя эти выражения в пределах от -b до +b, получим

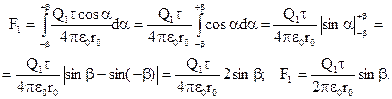
В силу симметрии расположения заряда Q₁ относительно стержня интегрирования второго выражения даёт нуль:

Таким образом, сила, действующая на заряд Q₁,

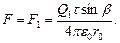(3)

Из рисунка следует, что 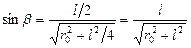. Подставив это выражение sinb в формулу (3). Получим

(4)

Произведём вычисления по формуле (4):

 

Пример 2. Электрическое поле создано бесконечной плоско­стью, заряженной с поверхностной плотностью s=400 нКл/м², и бесконечной прямой нитью, заряженной с линейной плотностью t = 100 нКл/м. На расстоянии r = 10 см от нити находится точечный заряд Q = 10 нКл. Определить силу, действующую на заряд, ее направление, если заряд и нить лежат в одной плоскости, параллельной заряженной плоскости.

Решение. Сила, действующая на заряд, помещенный в поле,

F = Eq, (1)

где Е — напряженность поля в точке, в которой находится за­ряд q.

Определим напряженность Е поля, создаваемого, по условию задачи, бесконечной заряженной плоскостью и бесконечной заря­женной нитью. Поле, создаваемое бесконечной заряженной плос­костью, однородно, и его напряженность в любой точке

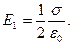(2)

Поле, создаваемое бесконечной заряженной линией, неоднород­но. Его напряженность зависит от расстояния и определяется по формуле

(3)

Согласно принципу суперпозиции элек­трических полей, напряженность поля в точке, где находится заряд Q, равна век­торной сумме напряженностей Е₁ и Е₂ , (рис. 14.5): Е= Е₁ + Е₂. Так как векто­ры Е₁ и Е₂ взаимно перпендикулярны, то

Подставляя выражения Е₁ и Е₂ по формулам (2) и (3) в это равенство, получим

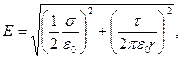или

Теперь найдем силу F, действующую на заряд, подставив вы­ражение Е в формулу (1):

(4)

Подставив значения величин Q, e₀, s, t, p и r в формулу (4) и сделав вычисления, найдем

F = 289 мкН.

Направление силы F, действующей на положительный заряд Q, совпадает с направлением вектора напряженности Е поля. Напра­вление же вектора Е задается углом а к заряженной плоскости. Из рисунка следует, что

tg a = , откуда a = arctg ().

Подставив значения величин s, t, p и r в это выражение и вычислив, получим

а = 51°34'.

 

Пример 3. Две концентрические про­водящие сферы радиусами R₁ = 6 см и R₂ = 10 см несут соответственно заряды Q₁= 1 нКл и Q₂ = - 0,5 нКл. Найти на­пряженность Е поля в точках, отстоящих от центра сфер на расстояниях r₁ = 5 см, r₂ = 9 см и r₃ = 15 см. Построить график Е(r}.

 

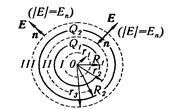Решение. Заметим, что точки, в которых требуется най­ти напряженности электрического поля, лежат в трех областях: область 1(r < R₁}, область II(R₁ < r₂ < R₂), область III(r₃ > R₂).

1. Для определения напряженности Е₁ в области I проведем сферическую поверхность S₁ радиусом r₁, и воспользуемся теоре­мой Остроградского — Гаусса. Так как внутри области I зарядов нет, то согласно указанной теореме получим равенство

(1)

где E_n — нормальная составляющая напряженности электрическо­го поля.

Из соображений симметрии нормальная составляющая Е_п долж­на быть равна самой напряженности и постоянна для всех точек сферы, т. е. E_n = E₁ = const.

Поэтому ее можно вынести за знак интеграла. Равенство (1) примет вид

Так как площадь сферы не равна нулю, то

E₁=0,

т. е. напряженность поля во всех точках, удовлетворяющих условию r₁ < R₁, будет равна нулю.

2. В области II сферическую поверхность проведем радиусом r₂. Так как внутри этой поверхности находится заряд Q₁, то для нее, согласно теореме Остроградского — Гаусса, можно записать равенство

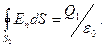(2)

Так как E_n = Е₂ == const, то из условий симметрии следует

или откуда

.

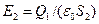Подставив сюда выражение площади сферы, получим

(3)

3. В области III сферическую поверхность проведем радиу­сом r₃. Эта поверхность охватывает суммарный заряд Q₁ + Q₂.Следовательно, для нее уравнение, записанное на основе теоремы Остроградского — Гаусса, будет иметь вид

Отсюда, использовав положения, примененные в первых двух случаях, найдем

(4)

Убедимся в том, что правые части равенств (3) и (4) дают единицу напряженности электрического поля:

Выразим все величины в единицах СИ (Q₁ =10^-9 Кл, Q₂ = - 0,5 ×10^-9 Кл, r₂ = 0,09 м, r₂ = 0,15 м, 1/(4pe₀) = 9 × 10⁹ м/Ф) и произведем вычисления:

Е₂ = 9×10⁹ В/м =1,11×10³ В/м =1,11кВ/м;

Е₃ = 9×10⁹ 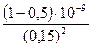В/м = 200В/м.

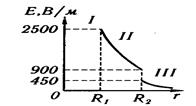4. Построим график Е(r). В области I (r₁ <.R₁) напряжен­ность Е = 0. В области II(R₁ £ r < R₂) напряженность Е₂(r) изменяется по закону 1/г². В точке r = R₁ напряженность E₂(R₁) = = 2500 В/м. В точке r = R₂ (r стремится к R₂ слева) E₂(R₂) = 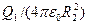= 900 В/м. В области III (r>R₂) Ез(r) изменяется по закону 1/r², причем в точке r = R₂ (r стремится к R₂ справа) E₃(R₂)= = 450 В/м. Та­ким образом, функция Е(r) в точках r = R₁ и r = R₂, терпит разрыв. График зависимости Е(r) представлен на рис.

Пример 4. По тонкой нити, изогнутой по дуге окружности радиусом R, равномерно распределен заряд с линейной плотностью t = 10 нКл/м. Определить напряженность Е и потенциал j электрического поля, создаваемого таким распределенным зарядом в точке О, совпадающей с центром кривизны дуги. Длина I нити составляет 1/3 длины окружности и равна 15 см.

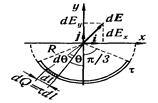Решение. Выберем оси координат так, чтобы начало координат совпадало с цен­тром кривизны дуги, а ось у была сим­метрично расположена относительно концов дуги. На нити выделим элемент длины dl. Заряд dQ = tdl, находящийся на выделенном участке, можно считать точеч­ным.

Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность dE поля, создаваемого зарядом dQ:

где r — радиус-вектор, направленный от элемента dl к точке, напряженность в которой вычисляется. Выразим вектор dE через проекции dEx и dEy на оси координат:

где i и j — единичные векторы направлений (орты). Напряженность Е найдем интегрированием:

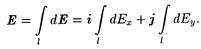
Интегрирование ведется вдоль дуги длины l. В силу симметрии интеграл dEx равен нулю. Тогда

где

Так как r=R=const и dl=Rdu, то

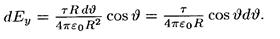
Подставим найденное выражение dEy в (1) и, приняв во внимание симметричное расположение дуги относительно оси Оу, пределы интегрирования возьмем от 0 до p/3, а результат удвоим:

Подставив указанные пределы и выразив R через длину дуги (3 l = 2pR), получим

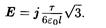
Из этой формулы видно, что вектор Е совпадает с положительным направлением оси Оу. Подставив значение т и l в последнюю формулу и сделав вычисления, найдем

Определим потенциал электрического поля в точке О. Най­дем сначала потенциал dj, создаваемый точечным зарядом dQ в точке О

Заменим r на R и произведем интегрирование:

Так как l = 2pR/3, то

Произведя вычисления по этой формуле, получим

Пример 5. Электрон без на­чальной скорости прошел раз­ность потенциалов U₀ = 10 кВ и влетел в пространство между пластинами плоского конденса­тора, заряженного до разности потенциалов U₁ = 100 В, по ли­нии АВ, параллельной пласти­нам. Расстояние d между пластинами равно 2см. Длина пластин конденсатора в направлении полета электрона равна 20 см. Определить расстояние ВС на экране Р, отстоящем от конденсатора на l ₂ = 1 м.

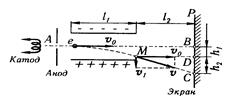Решение. Движение электрона внутри конденсатора склады­вается из двух движений:

1) по инерции вдоль линии АВ спостоянной скоростью v ₀, приобретенной под действием разности потенциалов U₀, которую электрон прошел до конденсатора;

2) равномерно ускоренного движения в вертикальном направлении к положительно заряженной пластине под действием постоянной силы поля конденсатора. По выходе из конденсатора электрон будет двигаться равномерно со скоростью v, которую он имел в точке М в момент вылета из конденсатора.

Из рисунка видно, что искомое расстояние

|ВС| = h₁ + h₂,

где h₁ — расстояние, на которое сместится электрон в верти­кальном направлении во время движения в конденсаторе; h ₂ — расстояние между точкой D на экране, в которую электрон попал бы, двигаясь по выходе из конденсатора по направлению началь­ной скорости v ₀, и точкой С, в которую электрон попадет в действительности.

Выразим отдельно h₁ и h ₂.

Пользуясь формулой длины пути равномерно ускоренного дви­жения, найдем

где а — ускорение, полученное электроном под действием поля конденсатора; t — время полета электрона внутри конденсатора.

По второму закону Ньютона а = F/m, где F — сила, с которой поле действует на электрон; т — его масса. В свою очередь, F = еЕ = eU₁ /d, где е — заряд электрона; U₁ — разность потен­циалов между пластинами конденсатора; d — расстояние между ними.

Время полета электрона внутри конденсатора найдем из фор­мулы пути равномерного движения t = v₀ t, откуда

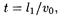
где t₁ — длина конденсатора в направлении полета электрона. Выражение скорости v ₀ найдем из условия равенства работы, со­вершенной полем при перемещении электрона, и приобретенной им кинетической энергии: mv /2 = eUo. Отсюда

Подставляя в формулу (1) последовательно значения а, F, t и v из соответствующих выражений, получим

Длину отрезка h₂ найдем из подобия треугольников MDC и векторного:

где v₁ — скорость электрона в вертикальном направлении в точке М; l₂, — расстояние от конденсатора до экрана.

Скорость v₁ найдем по формуле v₁ = at, которая с учетом выражений для а, F и t примет вид

Подставив выражение v₁ в формулу (3), получим

или, заменив v по формуле (3), найдем

Окончательно для искомого расстояния |ВС| будем иметь

Подставив значения величин U₁, Uo, d, l₁ и l₂ в последнее выражение и произведя вычисления, получим

Пример 6. Два плоских конденсатора одинаковой электроемко­сти С₁ = С₂ = С соединены в батарею последовательно и подключе­ны к источнику тока с электродвижущей силой ξ. Как изменится разность потенциалов U₁ на пластинах первого конденсатора, если пространство между пластинами второго конденсатора, не отклю­чая источника тока, заполнить диэлектриком с диэлектрической проницаемостью e = 7?

Решение. До заполнения второго конденсатора диэлектриком разность потенциалов на пластинах обоих конденсаторов была оди­накова: U₁ = U₂ = e /2. После заполнения электроемкость второго конденсатора возросла в e раз:

Электроемкость первого не изменилась, т. е. С = С. Так как источник тока не отключался, то общая разность по­тенциалов на батарее конденсаторов осталась прежней, она лишь перераспределилась между конденсаторами. На первом конденса­торе

где Q — заряд на пластинах конденсатора. Поскольку при после­довательном соединении конденсаторов заряд на каждой пластине и на всей батарее одинаков, то

где

Таким образом,

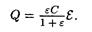
Подставив это выражение заряда в формулу (1), найдем

Чтобы найти, как изменилась разность потенциалов на пласти­нах первого конденсатора, вычислим отношение:

После подстановки значения e получим

Следовательно, разность потенциалов на пластинах первого кон­денсатора после заполнения второго конденсатора диэлектриком возросла в 1,75 раза.

Пример 7. Конденсатор электроемкостью C₁ = 3 мкФ был заряжен до разности потенциалов U₁ = 40 В. После отключения от источника тока конденсатор был соединен параллельно с дру­гим незаряженным конденсатором электроемкостью С₂ = 5 мкФ. Определить энергию DW, израсходованную на образование искры в момент присоединения второго конденсатора.

Решение. Энергия, израсходованная на образование искры, равна

где W₁ — энергия, которой обладал первый конденсатор до при­соединения к нему второго конденсатора; W₂, — энергия, которую имеет батарея, составленная из первого и второго конденсаторов.

Подставив в равенство (1) формулу энергии заряженного конденса­тора W = CU²/2 и приняв во внимание, что общая электроемкость параллельно соединенных конденсаторов равна сумме электроем­костей отдельных конденсаторов, получим

где С₁ и C₂ — электроемкости первого и второго конденсаторов; U₁ — разность потенциалов, до которой был заряжен первый конденсатор; U₂ — разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U₂ следующим образом: U₂ = . Подставив это выражение U₂, в формулу (2), получим

После простых преобразований найдем

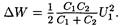
Выполнив вычисления, получим DW=1,5 мДж.

 

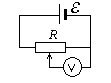Пример 8. Потенциометр с сопротивлёением 100 Ом подключен к источнику тока, ЭДС которого равна 150 В и внутреннее сопроти­вление r = 50 Ом. Определить по­казание вольтметра с сопротивлением R_B = 500 Ом, соединенного проводником с одной из клемм потенциометра и подвижным контактом с сере­диной обмотки потенциометра. Какова разность потенциалов между теми же точками потенциометра при отклю­ченном вольтметре?

Решение. Показание U₁ вольтметра, подключенного к точкам -A и B (рис.), определяется по формуле

 

где I₁ — сила тока в неразветвленной части цепи; R₁ — сопро­тивление параллельно соединенных вольтметра и половины потен­циометра.

Силу тока I₁ найдем по закону Ома для всей цепи:

где R — сопротивление внешней цепи.

Внешнее сопротивление R есть сумма двух сопротивлений:

Сопротивление R₁ параллельного соединения может быть най­дено по формуле,

,

откуда

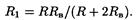
Подставив в эту формулу числовые значения величин и произ­ведя вычисления, найдем

Подставив в выражение (2) правую часть равенства (3), опре­делим силу тока:

Если подставить значения I₁ и R₁ в формулу (1), то найдем показание вольтметра:

Разность потенциалов между точками А и В при отключен­ном вольтметре равна произведению силы тока I₂, на половину сопротивления потенциометра, т. е. U₂ = I₂(R/2), или

Подставив сюда значения величин f, Л и г, получим

 

Пример 9. Сила тока в проводнике сопротивлением R=20 Ом нарастает в течение времени Dt = 2 с по линейному закону от I₀ = 0 до I_max = 6 А. Определить количество теплоты Q ₁, выделившееся в этом проводнике за первую секунду, и Q ₂ — за вторую, а также найти отношение этих количеств теплоты Q ₂/ Q ₁.

 

Решение. Закон Джоуля — Ленца Q = I²Rt применим в случае постоянного тока (I = const.). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно ма­лого промежутка времени и записывается в виде

Здесь сила тока I является некоторой функцией времени. В нашем случае

где k — -коэффициент пропорциональности, равный отношению приращения силы тока к интервалу времени, за который произо­шло это приращение:

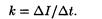
С учетом равенства (2) формула (1) примет вид

Для определения количества теплоты, выделившегося за конеч­ный промежуток времени Dt, выражение (3) следует проинтегри­ровать в пределах от t₁ до t₂.

При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t₁ = 0, t₂ = 1 с и, следовательно,

а за вторую секунду — пределы интегрирования t₁ = 1 с, t₂ = 2 с и тогда

Следовательно,

т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду.

Пример 10. Длинный провод с током I = 50 А изогнут под углом a = 2p/3. Определить магнитную индукцию В в точке А. Расстояние d = 5 см.

Решение. Изогнутый провод можно рас­сматривать как два длинных провода, концы которых соединены в точке О. В соответствии с принципом суперпозиции магнитных полей магнитная индукция В в точке А будет равна геометрической сумме магнитных индукций В₁ и В₂ полей, создаваемых отрезками длинных проводов 1 и 2, т. е. В = В₁ + В₂. Магнит­ная индукция B₂ равна нулю. Это следует из закона Био — Савара — Лапласа, согласно которому в точках, лежащих на оси проводника, dB = 0([d lr ] = 0).

Магнитную индукцию В₁ найдем, восполь­зовавшись формулой (3), полученной в при­мере 3:

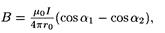
где r₀ — кратчайшее расстояние от провод­ника 1 до точки А

В нашем случае a₁ ® 0 (проводник длин­ный),

a₂ = a = 2p/3(cosa₂ = cos(2p/3)) = —1/2. Расстояние r₀ = dsin(p — a) = dsin(p/3) = d 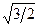. Тогда магнитная индук­ция

Так как В = В₁ (В₂ = 0), то

 

Вектор В сонаправлен с вектором B₁ и определяется правилом правого винта. На рис. 21.6 это направление отмечено значком х (перпендикулярно плоскости чертежа от нас).

Проверка единиц аналогична выполненной в примере 1.

Произведем вычисления:

Пример 11. По двум параллельным прямым проводам длиной l = 2,5 м каждый, находящимся на расстоянии d = 20 см друг от друга, текут одинаковые токи I=1 кА. Вычислить силу F взаимодействия токов.

Решение. Взаимодействие двух проводников, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой проводник. Предположим, что оба тока (обозначим их I₁ и I₂) текут в одном направлении.

Вычислим силу F_1,2, с которой магнит­ное поле, созданное током I₁, действует на проводник с током I₂. Для этого проведем магнитную силовую линию так (штриховая линия на рис.), чтобы она касалась проводника с током I₂. По касательной к силовой линии проведем вектор магнитной индукции B₁. Модуль магнитной индукции В₂ определяется соот­ношением

Согласно закону Ампера, на каждый элемент второго провод­ника с током I₂ длиной dl₂ действует в магнитном поле сила

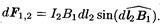
Так как отрезок dl перпендикулярен вектору B₁, то

и тогда

Подставив в выражение (2) В₁ из (1), получим

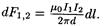
Силу F_1,2 взаимодействия проводников с током найдем инте­грированием по всей длине второго проводника:

Заметив, что I1 = I2 = I и l2 = l, получим

Убедимся в том, что правая часть этого равенства дает единицу силы (Н):

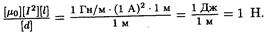
Произведем вычисления:

Сила.F_1,2 сонаправлена с силой dF_1,2 и определяется (в данном случае это проще) правилом левой руки.

Пример 12. Электрон, имея скорость v = 2 Мм/с, влетел в однородное магнитное поле с индукцией В = 30 мТл под углом а = 30° к направлению линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон.

 

Решение. Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца, перпендикулярная век­торам магнитной индукции В и скорости v частицы:

где Q — заряд частицы