(4.11)
Вторая строчка в определении (4.11) может быть использована в качестве признака принадлежности произвольной точки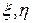 
базисному треугольнику 
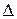. Произвольная функция 
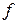со значениями 
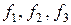может быть представлена на элементе 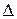разложением по базису:
. (4.12)
Градиенты линейных базисных функций (4.11) – это векторы
(4.13)
Обратим внимание, что градиенты линейных базисных функций не зависят от координат.
Коэффициенты элементных матриц выражаются через интегралы от базисных функций и их произведений. Поэтому вычислим следующие интегралы
,
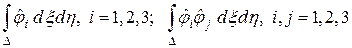а также интегралы от базисных функций и их произведений по границе.
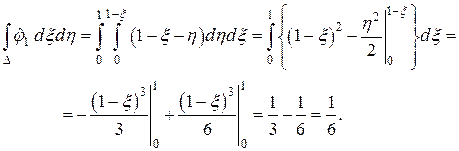
Аналогично получаем
.
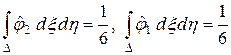Интегралы от произведений.
Аналогично вычисляются интегралы
.
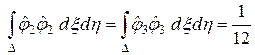Оставшиеся интегралы от произведения разных базисных функций равны
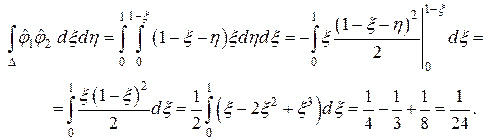
Аналогично
.
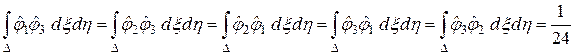Итак,
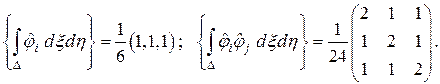(4.14)
Теперь, используя разложение (4.12) произвольной функции 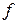по базису 
, легко подсчитать интеграл (4.9) этой функции по области:
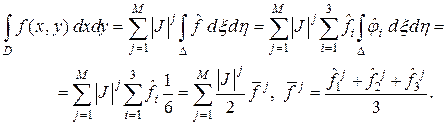(4.15)
Вторая формула (4.14) определяет матрицу масс (3.4):
(4.16)
Используя формулу (4.7), разложение (4.12) и градиенты базисных функций (4.13), выведем формулу дифференцирования произвольной функции .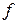
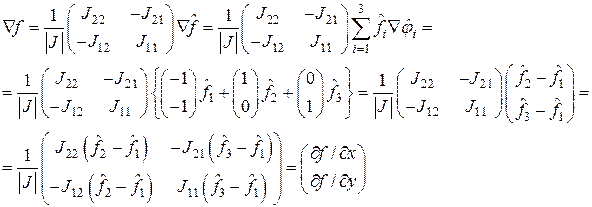(4.17)
Вспомним, что согласно (3.5) элементы матрицы жесткости определялись как
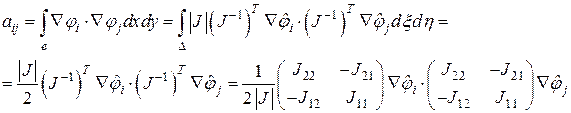
Вычислим вначале
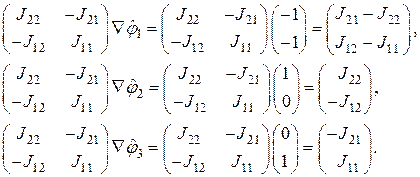
Теперь нетрудно подсчитать элементы матрицы жесткости, попарно перемножая скалярно выписанные вектора:
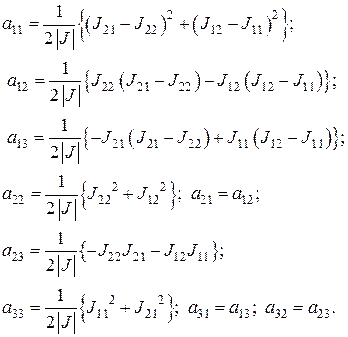(4.18)
Итак, все элементные матрицы и векторы, необходимые для сборки системы МКЭ, определены. Напомним, что в линейной алгебраической системе уравнений (4.3)
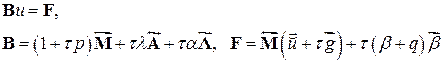(4.19)
матрица масс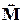 
собирается из элементных вкладов (4.16), матрица жесткости 
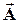состоит из элементов (4.18), компоненты матрицы 
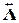определены в (3.7) интегралами по границе, вектора 
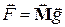и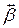 
состоят из компонент (3.8) и (3.9). Вспомним, как это выглядело для треугольника, у которого узлы 1 и 3 граничные:
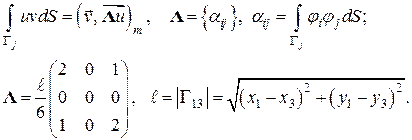(4.20)
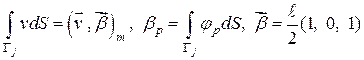(4.21)
Лекция 5. Программирование МКЭ
Структура данных
Нам необходимы глобальная матрица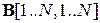 
и глобальный вектор 
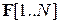системы МКЭ, а также вектор неизвестных узловых значений 
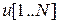. Здесь 
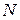‑ число узлов МКЭ сетки. Сразу отметим, что матрица 
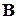разрежена, поэтому на практике хранят толко ее ненулевые элементы. Вопросы компактного хранения и алгебры разреженных матриц будут рассмотрены в следующем курсе, посвященном решению сеточных уравнений. Пока формально, для ясности понимания, будем использовать заполненные матрицы.
Type
float=extended;
TGlobMat=array[1..N;1..N] of float;
TGlobVec= array[1..N] of float;
sGlobMat=^TGlobMat;
sGlobVec=^TGlobVec;
Var
B:sGlobMat;
U,F: sGlobVec;
Сама сетка, как уже отмечалось, хранится в двух таблицах.
Type
TTable1=record
x,y:float;
b:integer;
end;
TTable2=record
n1,n2,n3:integer;
end;
arTab2=array[1..M] of TTable2;
arTab1= array[1..N] of TTable1;
sTab1=^arTab1;
sTab2=^arTab2;
Var
Tab1:sTab1;
Tab2:sTab2;
