Вектора и матрицы в интегральном тождестве (3.10) определены на каждом конечном элементе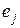 
и имеют размерности 
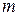и 
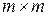по числу узлов в элементе. Для произвольного элементного вектора 
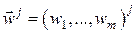определим расширенный элементный вектор 
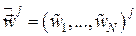длиной 
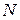(по числу узлов МКЭ-сетки), у которого отличны от нуля только 
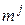компонент 
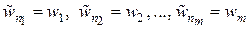. Например, для элемента 28 сетки, показанной на рис. 3.2, 
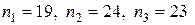(это записано в строке 28) таблицы связности. Поэтому компоненты элементного вектора 
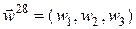образуют ненулевые компоненты расширенного элементного вектора
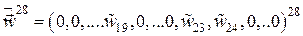
Аналогично для произвольной элементной матрицы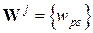 
размерности 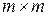определим расширенную элементную матрицу 
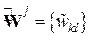размерностью 
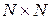, у которой отличны от нуля только 
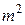компонентов, равных 
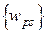и расположенных в позициях 
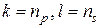. Для нашего треугольника 
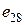это элементы
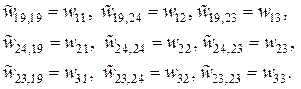
По существу, расширенные элементные вектора и матрицы получаются из элементных векторов и матриц рассылкой их элементов на нужные позиции в соответствии с глобальной нумерацией узлов элемента, определенной таблицей связности.
Замечательное свойство расширенных векторов и матриц определяется расположением в них нулей и выражается следующими равенствами
.
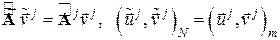Используя эти свойства, можно переписать интегральное тождество (3.10) а терминах расширенных векторов и матриц:
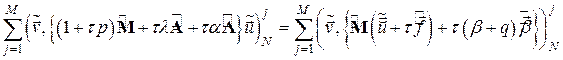(4.1)
Определим, далее, глобальные вектора и матрицы как сумму расширенных элементных векторов и матриц:
.
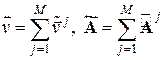В этих терминах можно переписать равенство (4.1) в виде
.
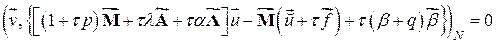Поскольку глобальный вектор 
в последнем равенстве может выбираться произвольно, то это значит, что выражение в фигурных скобках должно равняться нулю. Так мы приходим к глобальной системе уравнений МКЭ
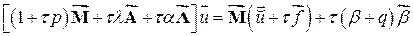(4.2)
или
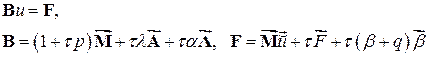(4.3)
Матрица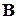 
этой системы складывается из глобальных матриц масс 
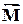, жесткости 
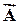и матрицы 
, порожденной граничными условиями 3-го рода. Каждая из этих матриц, в свою очередь, представляет собой сумму вкладов от соответствующих элементных матриц. Структура правой части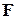 
уравнения (4.3) аналогична в том смысле, что также представляет собой сумму вкладов от всех элементных векторов. Такая структура системы уравнений МКЭ определяет алгоритм поэлементной сборки ее матрицы и правой части. Вначале все элементы глобальной матрицы 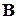и глобального вектора правой части 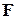обнуляются, затем в цикле по конечным элементам 
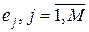вычисляются элементные матрицы и вектора и добавляются к соответствующим элементам 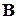и 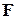. Это соответствие определено в таблице 2, где для каждого элемента 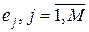указаны глобальные номера его узлов. Непосредственно из алгоритма сборки видно, что матрица 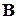будет разреженной: в ее 
-ую строку, соответствующую -му узлу сетки, очевидно попадут вклады от элементов, инцидентных данному узлу (список таких элементов содержится в таблице 4). При этом номера столбцов -ой строки, куда попадут эти вклады, совпадает со множеством глобальных номеров узлов инцидентных -му узлу сетки элементов. Эти номера и перечислены в -ой строке таблицы 3. Аналогично производится поэлементная сборка вектора 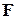правой части системы уравнений МКЭ.
Итак, чтобы собрать систему уравнений МКЭ нужно
1. Триангулировать область 
, т.е. построить МКЭ-сетку.
2. Определить базисные функции на каждом конечном элементе.
3. Вычислить элементные вклады с помощью интегралов (3.4), (3.5), (3.6), (3.7), (3.9).
4. Выполнить поэлементную сборку глобальных векторов и матриц.
Проблемы 1 и 4 нами решены, а задачи 2 и 3 решаются с помощью т.н. базисного элемента, на котором легко и однообразно вводятся базисные функции и выполняются операции дифференцирования и интегрирования.
