Самостоятельная подготовка

ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Дисциплина состоит из 2-х учебных модулей и экзамена.

Модуль 1

Таблица 5.1

Виды аудиторных занятий и самостоятельной работы	Сроки проведения или выполнения,недели	Трудоёмкость,часы	Примечание
Лекции	1-8
Упражнения	1-9
Домашние задания текущие	1-9
Контроль по модулю №1

Модуль 2

Таблица 5.2

Виды аудиторных занятий и самостоятельной работы	Сроки проведения или выполнения,недели	Трудоёмкость,часы	Примечание
Лекции	9-17
Упражнения	10-17
Домашние задания текущие	10-17
Контроль по модулю №2

Модуль 1: Интегралы

Лекции

Лекция 1. Первообразная и ее свойства. Неопределенный интеграл, его свойства, связь с дифференциалом. Таблица основных неопределенных интегралов. Интегрирование подстановкой и заменой переменного. Интегрирование по частям.

ОЛ-1, § 1.1–1.4; ОЛ-3, гл. X, § 1–3, § 10–14; ОЛ-5, гл. 5, § 5.1–5.2.

Лекция 2. Рациональные дроби. Разложение правильной рациональной дроби в сумму простейших (без док-ва). Интегрирование основных типов функций. Примеры интегралов, не выражающихся через элементарные функции.

ОЛ-1, § 1.1–1.6; § 3–4; ОЛ-1, § 2.1–2.4; ОЛ-3, гл. X, § 4–14, гл. VII § 1–2; ОЛ-5, гл. 5, § 3-5.

Лекция 3. Определенный интеграл как предел интегральных сумм. Теорема об интегрируемости кусочно-непрерывных функций (без док-ва). Геометрическая интерпретация определенного интеграла. Основные свойства определенного интеграла. Теоремы об оценке и о среднем значении.

ОЛ-1, § 6.1–6.2, 6.5–6.8; ОЛ-3, гл. XI, § 1–3; ОЛ-5, гл.6, § 6.1–6.2.

Лекция 4. Определенный интеграл с переменным верхним пределом, теорема о его производной. Формула Ньютона — Лейбница. Вычисление определенных интегралов подстановкой и по частям. Интегрирование периодических функций, интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат.

ОЛ-1, § 6.9–6.10; ОЛ-3, гл. XI, § 4–6; ОЛ-5, гл.6, § 6.3–6.4.

Лекции 5-6. Несобственные интегралы по бесконечному промежутку (I-го рода). Несобственные интегралы от неограниченных функций на отрезке (II-го рода). Признаки сходимости несобственных интегралов. Абсолютная и условная сходимости. Несобственные интегралы с несколькими особенностями.

ОЛ-1, § 7.1–7.6, 7.8; ОЛ-3, гл. XI, § 7; ОЛ-5, гл. 6, § 6.8–6.11.

Лекции 7-8. Вычисление площадей плоских фигур, ограниченных кривыми, заданными в декартовых координатах, параметрически и в полярных координатах. Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения. Вычисление длины дуги кривой и площади поверхности вращения.

ОЛ-1, § 9.1–9.5; ОЛ-3, гл. XII, § 1, 2, 4, 5; ОЛ-5, гл. 7, § 7.1–7.5.

Упражнения

Занятие 1. Непосредственное интегрирование по таблице. Интегрирование методом подстановки.

Ауд.: ОЛ-8, гл.6, §1: 6.15, 6.23, 6.24, 6.27, 6.29, 6.35, 6.37, 6.40, 6.42, 6.43, 6.44, 6.48 6.52, 6.53, 6.56, 6.60, 6.62, 6.65, 6.74, 6.79, 6.83, 6.89, 6.95, 6.98, 6.100, 6.102, 6.107 или

ОЛ-9, гл.4, §1: 1032, 1040, 1044, 1046, 1050, 1062, 1063, 1065, 1066, 1073, 1075, 1080, 1093, 1082, 1086, 1095, 1104, 1119, 1133, 1137, 1145, 1149,1153, 1159, 1163, 1167, 1179, 1189.

Дома: ОЛ-8, гл.6, § 1: 6.20, 6.22, 6.25, 6.32, 6.38, 6.39, 6.41 6.45, 6.46, 6.47, 6.49, 6.54, 6.57, 6.61, 6.66, 6.68, 6.72, 6.76, 6.80, 6.85, 6.86, 6.92, 6.97, 6.101, 6.104, 6.106, 6.112 или

ОЛ-9, гл.4, § 1: 1037, 1041, 1057, 1069, 1070, 1074, 1077, 1083, 1085, 1094, 1108, 1096, 1101, 1114, 1120, 1130, 1146, 1152, 1154, 1162, 1172 1182, 1188.

Занятие 2. Интегрирование по частям.

Ауд.: ОЛ-8, гл. 6, § 1: 6.129, 6.130, 6.132, 6.135, 6.124, 6.128, 6.136, 6.143, 6.151, 6.157, 6.144, 6.146, 6.147, 6.155, 6.156 или

ОЛ-9, гл. 4, § 3: 1214, 1219, 1236, 1231, 1213, 1223, 1227, 1234, 1235, 1252, 1253, 1245, 1237, 1228, 1242, 1246.

Дома: ОЛ-8, гл. 6, § 1: 6.125, 6.131, 6.140, 6.142, 6.127, 6.138, 6.145, 6.152, 6.153, 6.154, 6.137, 6.141 или

ОЛ-9, гл. 4, § 3: 1215, 1217, 1229, 1232, 1244, 1237, 1241, 1254, 1239, 1249, 1222, 1226.

Занятие 3. Интегрирование выражений, содержащих квадратный трехчлен.

Ауд.: ОЛ-8, гл. 6, § 2: 6.158, 6.161, 6.163, 6.165, 6.271, 6.250, 6.254, 6.255, 6.257, 6.259, 6.260, 6.264, 6.275 или

ОЛ-9, гл. 4, § 4: 1225, 1259, 1261, 1262, 1265, 1266, 1269, 1271, 1272, 1274, 1277, 1278, 1279.

Дома: ОЛ-8, гл. 6, § 2:, 6.159, 6.160, 6.162, 6.164, 6.251, 6.252, 6.253, 6.256, 6.258, 6.265, 6.280 6.276, 6.277 или

ОЛ-9, гл. 4, § 4: 1258, 1260, 1263, 1267, 1270, 1268, 1273, 1275, 1276.

Занятие 4. Интегрирование рациональных дробей.

Ауд.: ОЛ-8, гл. 6, § 2: 6.167, 6.168, 6.177, 6.171, 6.179, 6.178, 6.174, 6.185, 6.186, 6.188 или

ОЛ-9, гл. 4, § 5: 1282, 1284, 1286, 1289, 1290, 1298, 1308, 1313, 1314.

Дома: ОЛ-8, гл. 6, § 2: 6.129, 6.170, 6.173, 6.180, 6.181, 6.184, 6.187, 6.189 или

ОЛ-9, гл. 4, § 5: 1283, 1285, 1292, 1295, 1296, 1297, 1305, 1307, 1311.

Занятие 5. Интегрирование тригонометрических функций.

Ауд.: ОЛ-8, гл. 6, § 2: 6.190, 6.191, 6.195, 6.197, 6.198, 6.201, 6.203, 6.206, 6.209, 6.212, 6.213, 6.216 или

ОЛ-9, гл. 4, § 7: 1338, 1341, 1345, 1347, 1350, 1351, 1355, 1359, 1365, 1366.

Дома: ОЛ-8, гл. 6, § 2: 6.192, 6.194, 6.196, 6.199, 6.202, 6.204, 6.208, 6.210, 6.211, 6.214, 6.215, 6.217 или

ОЛ-9, гл. 4, § 7: 1339, 1340, 1344, 1346, 1348, 1352, 1358, 1362, 1367, 1368, 1372.

Занятие 6. Интегрирование тригонометрических функций. Интегрирование некоторых иррациональных функций.

Ауд.: ОЛ-8, гл. 6, § 2: 6.219, 6.222, 6.225, 6.226, 6.238, 6.240, 6.242, 6.244, 6.261, 6.262, 6.264, 6.266, 6.267 или

ОЛ-9, гл. 4, § 6, 7: 1377, 1382, 1388, 1380, 1389, 1318, 1320, 1322, 1325, 1403, 1405, 1407, 1411, 1412.

Дома: ОЛ-8, гл. 6, § 2: 6.218, 6.223, 6.224, 6.227, 6.239, 6.241, 6.243, 6.245, 6.263, 6.256, 6.268, 6.269 или

ОЛ-9 гл. 4 § 6, 7: 1373, 1378, 1381, 1389, 1387, 1315, 1317, 1319, 1321, 1323, 1324, 1404, 1406, 1408, 1413.

Занятие 7. Контрольная работа «Техника интегрирования».

Занятие 8. Вычисление определенного интеграла. Его свойства и геометрическая интерпретация.

Ауд.: ОЛ-8, гл. 6, § 4: 6.326, 6.337, 6.340, 6.346, 6.350, 6.379, 6.387, 6.390, 6.395, 6.399, 6.406, 6.364(б, в), 6.365 (а, в), 6.366 (а, г), 6.369, 6.370, 6.378 (в задачах 6.326, 6.337, 6.340, 6.399, 6.406 дать геометрическую интерпретацию) или

ОЛ-9, гл. 5, § 2, 4–6: 1521, 1529, 1534, 1536, 1538, 1576, 1587, 1590, 1592, 1598, 1592, 1598, 1599, 1600, 1610(а, б), 1611 (а, в), 1612, 1614, 1619, 1621 (в задачах 1521, 1529, 1536, 1599, 1600 дать геометрическую интерпретацию).

Дома: ОЛ-8, гл. 6, § 4: 6.328, 6.336, 6.341, 6.347, 6.386, 6.394, 6.400, 6.403, 6.464 (а), 6.365 (б), 6.366 (б, в), 6.368, 6.371 (в задачах 6.336, 6.338, 6.341, 6.399, 6.347 дать геометрическую интерпретацию) или

ОЛ-9, гл.5, § 2, 4–6: 1522, 1527, 1537, 1539, 1541, 1589, 1591, 1593, 1601, 1602, 1610 (в), 1611 (б), 1613, 1618, 1620 (в задачах 1527, 1537, 1541, 1601 дать геометрическую интерпретацию).

Занятие 9. Вычисление площадей плоских фигур в декартовой и полярной системах координат.

Ауд.: ОЛ-8, гл. 6, § 6: 6.453, 6.456, 6.467, 6.478, 6.479, 6.483, 6.486, 6.488 или

ОЛ-9, гл. 5, § 7: 1623, 1624, 1633, 1638, 1650, 1655, 1658, 1663.

Дома: ОЛ-8, гл. 6, § 6: 6.457, 6.464, 6.468, 6.480, 6.481, 6.484, 6.487, 6.492 или

ОЛ-9, гл. 5, § 7: 1626, 1634, 1636, 1645, 1653, 1656, 1657, 1661.

Занятия 10-11. Несобственные интегралы. Исследование несобственных интегралов на сходимость. Вычисление объемов тел по площадям поперечных сечений, вычисление объемов тел вращения. Приложения определенного интеграла в физике.

Ауд.: ОЛ-8, гл. 6, § 5, 6: 6.411, 6.417, 6.419, 6.424, 6.433, 6.435, 6.437, 6.441, 6.426, 6.428, 6.430, 6.432, 6.443, 6.445, 6.447, 6.449, 6.451, 6.533, 6.535, 6.536, 6.538, 6.540, 6.541, 6.543, 6.560, 6.573, 6.581 или

ОЛ-9, гл.5, § 3, 9: 1551, 1552, 1555, 1556, 1560, 1562, 1546, 1549, 1550, 1558, 1559, 1570, 1573, 1571, 1707, 1708, 1688, 1691, 1692, 1694, 1701 (в), 1702, 1703.

Дома: ОЛ-, гл. 6, § 5, 6: 6.412, 6.418, 6.420, 6.434, 6.436, 6.439, 6.429, 6.431, 6.442, 6.444 6.446, 6.448, 6.534, 6.537, 6.542, 6.544, 6.561, 6.574, 6.582 или

ОЛ-9, гл. 5, § 3, 9: 1554, 1559, 1563, 1565, 1547, 1557, 1566, 1567, 1572, 1646, 1683, 1691 (а), 1697, 1709, 1689, 1695, 1697, 1701 (б) 1704.

Занятия 12-13. Вычисление длины дуги и площади поверхности вращения.

Ауд.: ОЛ-8, гл. 6, § 6: 6.494, 6.500, 6.506, 6.507, 6.509, 6.519 (а), 6.523 (б), 6.527, 6.530 или

ОЛ-9, гл.5, § 8, 10: 1665, 1667, 1669, 1676, 1680, 1715, 1722 (б), 1723 (в), 1725.

Дома: ОЛ-8, гл. 6, § 6: 6.499, 6.504, 6.511, 6.519 (б), 6.523 (а), 6.526, 6.529, 6.531 или

ОЛ-9 гл. 5 § 8, 10: 1666 1670, 1678, 1679, 1716, 1722(а), 1723(б), 1726.

Занятие 14. Контроль по модулю 1 (РК №1).

Модуль 2: Дифференциальные уравнения

Лекции

Лекция 1. Обыкновенное дифференциальное уравнение (ОДУ) первого порядка, его решения. Частное и общее решения. Интегральные кривые. Задача Коши для ОДУ первого порядка. Теорема Коши о существовании и единственности решения ОДУ (без вывода). Решение ОДУ первого порядка: с разделяющимися переменными, однородные ОДУ, линейные ОДУ (однородные и неоднородные), уравнения Бернулли. Геометрическая интерпретация ОДУ первого порядка. Изоклины. Геометрическое решение ОДУ с помощью изоклин.

ОЛ-2, § 1.1-1.3, 2.1, 2.2, 2.4, 3.1–3.4; ОЛ-4, гл. ХШ, § 1–5, 7–9, 3, 11, 12; ОЛ-6, гл. 1, § 1.1, 1.2, 1.3, 1.4.

Лекция 2. ОДУ n-го порядка. Частное и общее решения. Задача Коши для ОДУ n-го порядка и ее геометрическая интерпретация (при n=2). Теорема Коши о существовании и единственности решения ОДУ (без док-ва). Краевая задача. Понижение порядка некоторых типов ОДУ n-го порядка.

ОЛ-2, § 4.4, 11.1, 11.2; ОЛ-4, гл. XIII, § 16–18; ОЛ-6 гл.1, § 1.11, 1.13, 1.14.

Лекции 3-4. Линейные дифференциальные уравнения (ЛДУ) n-го порядка, уравнения однородные и неоднородные. Теорема о существовании и единственности решения. Дифференциальный оператор L[y], его свойства. Линейное пространство решений однородного ЛДУ. Линейно зависимые и независимые системы функций на отрезке. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно зависимых функций. Теорема о вронскиане системы линейно независимых решений однородного ЛДУ. Теорема о структуре общего решения однородного ЛДУ. Размерность пространства решений и фундаментальная система решений однородного ЛДУ. Формула Остроградского — Лиувилля и ее следствия. Понижение порядка однородного ЛДУ при известном частном решении.

ОЛ-2, § 6.1–6.3; ОЛ-4, гл. XIII, § 20; ОЛ-6, гл.1, § 1.15.

Лекции 5-6. Однородные ЛДУ с постоянными коэффициентами. Характеристическое уравнение однородного ЛДУ. Построение общего решения по корням характеристического уравнения (вывод для n=2). Неоднородные ЛДУ, структура их общего решения. Теорема о наложении частных решений. Метод Лагранжа вариации постоянных (вывод для n=2). Нахождение частного решения неоднородного ЛДУ с постоянными коэффициентами и правой частью специального вида.

ОЛ-2, § 6.2, 6.4–6.6; ОЛ-4, гл. XIII, § 21–25; ОЛ-6, гл.1, § 1.16–1.18.

Лекция 7. Нормальные системы ОДУ. Задача и теорема Коши для системы ОДУ. Частное и общее решения системы ОДУ. Сведение ОДУ высшего порядка к нормальной системе ОДУ первого порядка и сведение нормальной системы ОДУ первого порядка к ОДУ высшего порядка (вывод для n=2). Первые интегралы системы. Понижение порядка системы ОДУ при помощи первых интегралов. Интегрируемые комбинации. Симметрическая форма записи нормальной автономной системы ОДУ.

ОЛ-2, § 4.1, 4.2, 6.1, 8.1–8.4; ОЛ-4, гл. XI, § 29, ОЛ-6, гл.1, § 1.19, 1.22

Лекции 8-9. Системы линейных ОДУ первого порядка. Определитель Вронского. Фундаментальная система решений. Формула Остроградского — Лиувилля. Теоремы о структуре общего решения однородной и неоднородной систем линейных ОДУ первого порядка. Метод вариации постоянных. Однородные системы линейных ОДУ с постоянными коэффициентами. Характеристическое уравнение системы. Построение общего решения по корням характеристического уравнения (вывод только для случая действительных и различных корней).

ОЛ-2, § 5.1–5.7; 6.; ОЛ-4, гл. XIII, § 30, ОЛ-6, гл.1, § 1.20-22.

Упражнения

Занятие 1. ОДУ первого порядка, его решение. Геометрическое решение ОДУ первого порядка методом изоклин. Интегрирование ОДУ с разделяющимися переменными и однородных ОДУ.

Ауд.: ОЛ-8, гл.9, §1: 9.1, 9.4, 9.9, 9.18, (решить методом изоклин), 9.27, 9.30, 9.33, 9.35, 9.39, 9.44, 9.48, 9.49, 9.55, 9.64, 9.65 или

ОЛ-9 гл.9, §1,3,4,9: 2706, 2719, 2737, (решить методом изоклин), 2742, 2744, 2746, 2748, 2750, 2770, 2772, 2775, 2848, 2852.

Дома:ОЛ-8, гл.9, §1:9.3, 9.6, 9.12, 9.20, 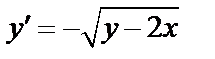(решить методом изоклин), 9.22, 9.26, 9.28, 9.34, 9.36, 9.40, 9.45, 9.47, 9.51, 9.53, 9.66 или

ОЛ-9, гл.9, §1, 3, 4, 9: 2708, 2720, 2736, 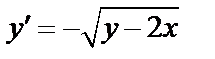(решить методом изоклин), 2743, 2745, 2747, 2769, 2771, 2773, 2873, 2834, 2840, 2857, 2874.

Занятие 2. Интегрирование линейных ОДУ первого порядка и уравнений Бернулли.

Ауд.: ОЛ-8, гл.9, § 1: 9.67, 9.72, 9.74, 9.78, 9.83, 9.88, 9.91, 9.92, 9.95 или

ОЛ-9 гл.9 §5, 9: 2785, 2787, 2789, 2791, 2793, 2794, 2847, 2850, 2854, 2881.

Дома: ОЛ-8 гл. 9 § 1: 9.68, 9.69, 9.75, 9.79, 9.80, 9.84, 9.87, 9.93, 9.94 или

ОЛ-9 гл. 9 § 5, 9: 2786, 2790, 2792, 2795, 2844, 2856, 2858, 2866.

Занятие 3. ОДУ высших порядков, основные понятия. Интегрирование уравнений, допускающих понижение порядка.

Ауд.: ОЛ-8, гл. 9, § 2: 9.202, 9.210, 9.214, 9.215, 9.216, 9.229, 9.239, 9.247, 9.251, 9.273 или

ОЛ-9, гл. 9, § 10: 2910, 2926, 2935, 2921, 2938, 2943, 2945, 2950, 2951, 2966.

Дома: ОЛ-8 гл. 9 § 2: 9.203, 9.208, 9.213, 9.220, 9.223, 9.237, 9.238, 9.248, 9.249, 9.271 или

ОЛ-9, гл. 9, § 10: 2918, 2919, 2923, 2327, 2940, 2941, 2952, 2953, 2947, 2965.

Занятие 4. Контрольная работа «Дифференциальные уравнения первого порядка».

Занятие 5. Интегрирование линейных однородных ОДУ высших порядков с постоянными коэффициентами. Фундаментальная система решений, восстановление линейного однородного ОДУ по фундаментальной системе решений.

Ауд.: ОЛ-8, гл. 9, §2: 9.286, 9.291, 9.293, 9.294, 9.324, 9.322, 9.337, 9.327, 9.333, 9.336, 9.339, 9.296, 9.300, 9.298 или

ОЛ-9, гл.9, § 11–13: 2968 (а, в, е, д), 2976, 2983, 2987, 3045, 3051, 3057, 3052, 2969 (а, в, г).

Дома: ОЛ-8, гл.9, § 2: 9.288, 9.289, 9.295, 9.325, 9.326, 9.328, 9.330, 9.332, 9.334, 9.338, 9.299, 9.301 или

ОЛ-9, гл.9, § 11–13: 2968 (б, г, д), 2981, 2982, 3055, 3056, 3048, 3049, 2969 (б).

Занятие 6. Интегрирование линейных неоднородных ОДУ с постоянными коэффициентами и специальной правой частью.

Ауд.: ОЛ-8, гл.9, § 2: 9.346, 9.349, 9.352, 9.354, 9.357, 9.360, 9.366, 9.373, 9.369, 9.371, 9.376 или

ОЛ-9 гл.9, § 12, 13: 2994 (а, в, д), 2999 3004, 3000, 3016, 3019, 3064, 3062, 3063, 3067.

Дома: ОЛ-8, гл.9, § 2: 9.347, 9.349, 9.350, 9.353, 9.355, 9.361, 9.362, 9.370, 9.372, 9.374 или

ОЛ-9, гл.9, § 12, 13: 2994 (б, г, е), 3003, 3002, 2995, 3018, 3012, 3060, 3061, 3065.

Занятие 7. Интегрирование линейных неоднородных ОДУ высшего порядка методом вариации произвольных постоянных.

Ауд.: ОЛ-8, гл. 9, § 2: 9.342, 9.344, 9.381, 9.383, 9.308, 9.310 проинтегрировать уравнения (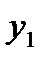 - частное решение соответствующего однородного уравнения):

а) , ;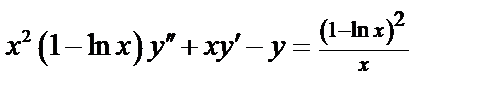

б) , .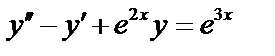

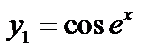в) или

ОЛ-9, гл. 9, § 11–13: 3033, 3035, 3038 (а), 3066, 2971, 2973, задачи а), б), в) (см. выше).

Дома: ОЛ-8, гл. 9, § 2: 9.343, 9.345, 9.385, проинтегрировать уравнения (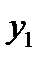 - частное решение соответствующего однородного уравнения):

а) , ;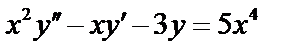

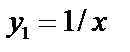б) , ;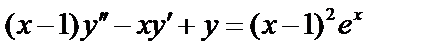

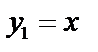в) 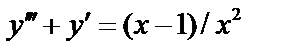или

ОЛ-9, гл. 9, § 11–13: 3032, 3034, 3037, 2972, 2974, 2975, задачи а), б), в) (см. выше).

Занятие 8. Интегрирование нормальных систем ОДУ первого порядка сведением к дифференциальному уравнению высшего порядка.

Ауд.: ОЛ-8, гл. 9, § 3: 9.402, 9.409, 9.412, 9.413, 9.417, 9.429 или

ОЛ-9 гл. 9 § 15:, 3079, 3080, 3087, 3088 (а, б), 3090.

Дома: ОЛ-8, гл.9, § 3: 9.403, 9.410, 9.414, 9.415, 9.419, 9.420, 9.428, 9.430 или

ОЛ-9, гл.9, § 15: 3078, 3083, 3085, 3088 (в), 3089.

Занятие 9. Интегрирование систем линейных однородных ОДУ с постоянными коэффициентами. Общее решение. Фундаментальная система решений.

Ауд.: ОЛ-8, гл. 9, § 3: 9.431, 9.433, 9.435.

Дома: ОЛ-8, гл.9, § 3: 9.432, 9.434, 9.436.

Занятие 10. Контроль по модулю 2 (РК №2).

Занятие 11. Интегрирование систем линейных неоднородных ОДУ первого порядка методом вариации постоянных.

Ауд.: ОЛ-8, гл. 9, § 3: 9.441, 9.443, 9.445.

Дома: ОЛ-8, гл.9, § 3: 9.442, 9.444, 9.448.

Самостоятельная подготовка

Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий, подготовке к контрольным работам и рубежным контролям.