Принципы функционирования и использования MATLAB. Структура языка.
Настройка рабочей среды, шрифты, текущая директория. Система помощи. Типы данных. Арифметические операции над числами. Логические операции, операции отношения. Стандартные функции. Массивы символов и тип данных char. Простейшие вычисления. Работа с матрицами и векторами. Двоеточие и множественная индексация. Многомерные матрицы.
Настройка окна, шрифты, текущая директория

Рис. 2.1. Настройка рабочей среды MATLAB

Рис. 2.2. Шрифты

Рис. 2.3. Установка текущей директории.
Система помощи
Среда MATLAB обладает многоуровневой справочной системой, которая позволяет получить информацию как по самой MATLAB, так и по всем ее приложениям. Получить доступ к справочной информации MATLAB можно различными способами:
- введя в командную строку соответствующую справочную команду или функцию;
- с помощью команд меню Help;
- щелкнув на кнопке со знаком вопроса на панели инструментов основного окна MATLAB.
MATLAB имеет интерактивную справочную систему, которая реализуется в командном режиме с помощью ряда команд. Одной из них является команда
>> help
которая выводит весь список папок (каталогов), содержащих m-файлы с определениями операторов, функций и иных объектов (рис. 2.4). Этот список дает представление о пакетах прикладных программ, расширяющих возможности системы MATLAB и содержащих примеры применения системы.

Рис. 2.4
При вводе команды
>> help elfun
в командное окно выводится список встроенных элементарных функций (рис. 2.5).

Рис. 2.5
Для получения справочной информации по любой из них требуется выполнить команду help <имя функции>, например,
>> help asinh
или
>> help /
Если в командной строке набрать команду doc elfun, то при этом перейдем в главное окно Help внутренней справочной системы MATLAB, в правой половине которого будет открыта первая страница документа справочной информации с указанным заголовком. Для получения справки по конретной функции необходимо выбрать вкладку с одноименным названием и щелкнуть на ней левой кнопкой мыши. Для получения более полной информации, снабженной графиками и лучше отформатированной, надо выполнить команду doc <имя функции>, например, (рис. 2.6)
>> doc asinh

Рис. 2.6
При вызове окна справки Help по умолчанию в нем отображается перечень ссылок на описания Toolboxes (рис. 2.7). Каждый раздел имеет подраздел Getting Started (Начало), который кратко знакомит с содержимым этого раздела, а также подраздел Examples (Примеры) (рис. 2.8).
Примеры могут содержать листинги программ MATLAB, которые можно просмотреть и запустить на выполнение. Для работы с текстом примера нужно щелкнуть на кнопке Open this Example (Открыть этот пример) на странице с примером. Примеры могут представлять собой видеоролики или видеоуроки, демонстрирующие, как пользоваться тем или иным инструментом.
Выделив текст левой клавишей мыши, можно с помощью контекстного меню вызвать выделенный фрагмент на исполнение, выбрав пункт Evaluate Selection (рис. 2.9).
Использование команд справки является быстрым способом получения информации, если вы точно знаете, что ищете и как это называется.
Например: doc ops – выводит информацию по разделу операторов и специальных символов; doc function – выводит информацию о назначении и создании файл-функций.

Рис. 2.7

Рис. 2.8
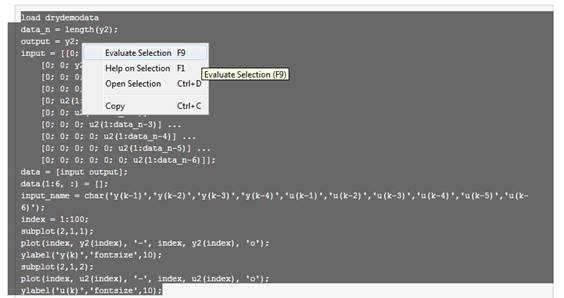
Рис. 2.9
Строка поискового запроса в системе помощи находится в верхней правой части окна. Например, чтобы найти варианты решения уравнение Ван-дер-Поля y''-μ(1-y2)y'+y=0, можно набрать в строке поискового запроса "Van der Pol" и выбрать один из результатов (в нашем случае наиболее подходящим, очевидно, является описание подраздела "Ordinary Differential Equations" из раздела "MATLAB > Mathematics > Numerical Integration and Differential Equations", внизу которого находится четыре примера решения вышеуказанного дифференциального уравнения)
Типы данных. Арифметические операции над числами. Логические операции, операции отношения.
Число – простейший объект системы MATLAB, представляющий количественные данные. Основным типом данных, с которым производятся вычисления в системе MATLAB, являются десятичные числа. Они приближают с заданной точностью произвольные вещественные (действительные) числа. Десятичные числа, используемые в MATLAB, могут быть целыми и дробными.
0
1
-93
7.5674
0.00000047
Возможно представление чисел в экспоненциальной форме с указанием мантиссы и порядка числа.
3.3333e-4
-75.8e13
Для отделения порядка числа от мантиссы применяется символ e, т.е. запись 3.3333e-04 соответствует записи 3.3333×10-4 или 0.00033333.
Ввод чисел возможен в любом удобном для пользователя виде. Например, проще набрать 10e8 или 1.0e9, чем 1 000 000 000, а результат будет тот же самый. Пробел между цифрами и символом e при вводе не допускается, так как это приводит к сообщению об ошибке:
>> 10 e8
??? 10 e8
Error: Missing operator, comma, or semicolon.
В качестве разделителя целой и дробной частей числа используется точка, а не запятая. При вводе числа с нулевой целой частью ноль может опускаться:.5 равнозначно 0.5.
Хотя задавать вещественные числа можно в любой из указанных выше форм, на машинном уровне системы MATLAB они представляются в форме с мантиссой и показателем степени. Этот основной тип данных называется double (формат с двойной точностью). Он задается по умолчанию, и даже целые числа представляются системой MATLAB на машинном уровне в той же форме, что и дробные числа.
Под мантиссу и показатель степени (на машинном уровне используется двоичная система записи) отводится 8 байт памяти. В результате для десятичных чисел достигается точность порядка 15 значащих цифр. Они принимает по модулю значения от 2.2250738507201e-308 до 1.797693134862316e+308. Для этих чисел зарезервированы имена realmin и realmax.
Все операции над числами MATLAB выполняет по умолчанию в формате double. Такой формат удовлетворяет подавляющему большинству требований к численным расчетам, но совершенно не подходит для символьных вычислений с произвольной (абсолютной) точностью. В MATLAB также существует тип данных single, который снижает требования к памяти в два раза (под мантиссу и показатель степени отводится 4 байта). Но при сложных вычислениях в этом случае возрастает вероятность получить результат с большой погрешностью.
Существуют и целые типы данных: int8, uint8, int16, uint16, int32, uint32, int64, uint64, под которые отводится 8, 16, 32 и 64 бита соответственно.Буква u соответствует беззнаковым типам данных с диапазоном от 0 до некоторого максимального положительного значения.
– int8 – тип данных использующийся для представления целых чисел с использованием 8 бит памяти. Тип имеет знак и может принимать значения от -128 до +127 (т.е -27 до 27 - 1).
– uint8 – тип аналогичный int8, но не имеющий знаки и принимающий значения от 0 до 255 (28 - 1).
Для того, чтобы переменная получила тип данных, отличный от double, применяется явный квалификатор, совпадающий с названием типа.
Например,
>> x=int32(3.2)
определяет переменную целого типа int32.
Подробную информацию о перечисленных типах данных можно получить по справкам doc double, doc single, doc int8, doc uint8.
При попытке записать в целочисленную ячейку вещественное число система произведет его округление по всем правилам:
>>e=int8(2.2)
e=
>>e=int8(2.8)
e=
Как отмечалось выше MATLAB работает с массивами и даже любое «одиночное число» с любым типом будет рассматриваться системой как массив из одного элемента:
>>e=[2]
e=
Формат числа определяет вид результата вычислений в командном окне. Чтобы не перегружать подробностями командное окно, MATLAB по умолчанию использует формат short (укороченный), при котором на экране отображаются только четыре цифры после десятичной точки. Однако формат вывода может быть и другим. Он может быть установлен с помощью изменения параметров Command Window. Выберем в меню пункт Preferences (Предпочтения). На экране появится диалоговое окно Preferences, изображенное на рис. 2.10.

Рис. 2.10
Для установки формата вывода следует убедиться, что в списке левой панели выбран пункт Command Window (как показано на рис. 2.10). Задание формата производится из раскрывающегося списка Numeric format панели Text display. Выберем short в раскрывающемся списке Numeric format. Закроем диалоговое окно, нажав кнопку ОК. Сейчас установлен короткий формат с плавающей точкой для вывода, при котором на экране отображаются только четыре цифры после десятичной точки. Наберем в командной строке 200/3 и нажмем <Enter>. Результат выводится в формате short:
>> 200/3
ans =
66.6667
Этот формат вывода сохранится для всех последующих вычислений, если только не будет установлен другой формат. В MATLAB возможна ситуация, когда при отображении слишком большого или малого числа результат не укладывается в формат short. При вычислении 100000/3 и 1/3000 результаты выводятся в экспоненциальной форме:
>> 100000/3
ans =
3.3333e+004
>> 1/3000
ans =
3.3333e-004
Однако, первоначальная установка формата short сохраняется при дальнейших вычислениях. Если требуется получить результат вычислений более точно, то в раскрывающемся списке диалогового окна Preferences следует выбрать long. При этом результат будет отображаться в длинном формате с плавающей точкой long с четырнадцатью цифрами после десятичной точки. Форматы short e и long e предназначены для вывода результата в экспоненциальной форме с четырьмя и четырнадцатью цифрами мантиссы после десятичной точки соответственно. Информацию о форматах можно получить, набрав в командной строке команду doc format.
Задать формат вывода можно непосредственно из командной строки при помощи команды format. Например:
>> format long e
>> 1.33/5.13
ans =
2.592592592592593e-001
>> format long g
>> ans
ans =
0.259259259259259
>> format rat
>> 0.03333333
ans =
1/30
Отметим, что format rat устанавливает формат вывода, при котором вещественные числа приближённо представляются отношением двух небольших целых чисел.
Для того, чтобы выделить результат, MATLAB выводит его через строку после вычисляемого выражения. Иногда требуется разместить больше строк на экране. Для этого в диалоговом окне Preferences следует выбрать compact из раскрывающегося списка Numeric display. В приводившихся ранее примерах пустой строки нет. Добавление пустых строк обеспечивается выбором loose из списка Numeric display.
Применение команды format без параметров восстанавливает используемое по умолчанию состояние format short и format loose.
Все промежуточные вычисления MATLAB производит с двойной точностью, независимо от того, какой формат вывода установлен.
Переменные – это именованные объекты, хранящие какие-либо данные. Переменные могут быть числовыми, матричными или символьными, что зависит от типа хранящихся в них данных. Типы переменных заранее не декларируются. Они определяются выражением, значение которого присваиваивается переменной, т.е. пользователь не должен заботиться о том, какие значения будет принимать переменная (комплексные, вещественные или целые).
Имя переменной (ее идентификатор) может содержать до 63 символа (MATLAB 2014a, см. функцию namelengthmax) и не должно совпадать с именами других переменных, функций, команд и системных переменных MATLAB. Последнее, что следует знать при задании переменных – это правило определения их имен. В MATLAB имена переменных могут задаваться только латинскими буквами, цифрами и символом ‘_’. Причем, первый символ в имени должен соответствовать букве латинского алфавита (см. функцию genvarname). Также следует отметить, что имена
arg = 1;
Arg = 2;
ARG = 3;
это три разных имени, т.е. три разные переменные со значениями 1, 2 и 3 соответственно. MATLAB различает регистр в именах переменных.
При программировании лучше всего задавать осмысленные имена переменных, по которым можно было бы понять какие данные они представляют. Это позволяет избежать путаницы при построении больших программ.
В MATLAB существует несколько имен переменных, являющихся зарезервированными. Переменные с такими именами называются системными. Они задаются после загрузки системы и могут использоваться в арифметических выражениях. Системные переменные могут быть переопределены, т.е. при необходимости им можно присвоить другие значения.
Ниже перечислены основные системные переменные MATLAB.
- ans – результат вычисления последнего не сохраненного пользователем выражения.
- i, j – мнимая единица (), используемая для задания мнимой части комплексных чисел.
- Inf (infinity) – обозначение машинной бесконечности.
- NaN – сокращение от слов Not-a-Number (не число), принятое для обозначения неопределенного результата (например, 0/0 или Inf/Inf).
- pi – число π (p=3,141592653589793).
- eps – погрешность операций над числами с плавающей точкой, т.е интервал между числом 1.0 и следующим ближайшим числом с плавающей точкой равен 2.2204e-16.
- realmin – минимальное по модулю вещественное число (2.2251e-308).
- realmax – наибольшее по модулю вещественное число (1.7977e+308).
Помимо числовых форматов существует и строковый формат представления информации. Тип char отвечает за это. Строковый тип данных это массив символов. При работе со строкой необходимо использовать все правила работы с массивами, но с поправкой на символы.
>> name=char('123')
name =
Комплексные числа в системе MATLAB записываются в следующем виде:
3+2i; 7-4j; -3.8952+1.23e-5i; 5+i*7.
Функции real и imag выделяют вещественную и мнимую части комплексного значения:
>> real(z)
ans =
-9
>> imag(z)
ans =
Функция complex формирует комплексное число по паре вещественных:
>> z=complex(3,-4)
z =
3.0000 - 4.0000i
Функция conj возвращает комплексно–сопряженное число:
>> conj(z)
ans =
3.0000 + 4.0000i
Такой же результат получим, поставив апостроф после комплексного значения:
>> z=1+2*i'
z =
1.0000 - 2.0000i
>> z'
ans =
1.0000 + 2.0000i
abs(x) - вычисляет модуль числа х
angle(x) - возвращает аргумент (в радианах) числа, но надо следить за квадрантом куда попадает число, т.к. среда использует arctg
isreal(x) - проверяет число на его принадлежность к классу вещественных числе, возвращает 1 (истину) если это так, иначе (х – комплексное число) возвращает ложь (0)
При работе с комплексными числами можно использовать соотношение Эйлера, т.е. записав число в экспоненциальной форме можно получить (нажав Enter) это же число, но в алгебраической записи. При этом надо помнить что угол указывается в радианах.
>> 5*exp(-j*pi/6)
ans =
4.3474 - 2.4699i
Рассмотрим базовые арифметические операции над простыми переменными в MATLAB. Пусть заданы две переменные a и b. Тогда операции сложения, вычитания, умножения и деления запишутся так:
c = a+b; % сложение
c = a-b; % вычитание
c = a*b; % умножение
c = a/b; % деление
Дополнительно, в MATLAB определена операция возведения в степень, которая записывается так:
c = a^2; % возведение переменной a в квадрат
c = a^0.5; % извлечение квадратного корня из переменной a
Приоритет арифметических операций * и / выше операций + и -, т.е. сначала выполняется умножение и деление, а затем, сложение и вычитание. Операция возведения в степень имеет наивысший приоритет. Для изменения приоритетов арифметических операций используются круглые скобки, как и в обычной математике, например,
c = 7+2*2; % значение c = 28
c = (7+2)*2; % значение с = 18
Использование деления слева на право. Это деление отличается записью наклонной черты. Привычное нам деление записывается «/», а это деление записывается «\». Поясним на примере вычисления:
>> 8\2
ans =
0.2500
>> 8/2
ans =
Т.е. в первом случае как раз и использовано деление о котором идет речь, записанное выражение эквивалентно нашим обычным «двум восьмым», т.е. четверти, что и показало вычисление.
Логические операторы MATLAB:
& - логическое И
| - логическое ИЛИ
~ - логическое НЕ
Операции отношения
| a < b | Истинно, если переменная a меньше переменной b и ложно в противном случае. |
| a > b | Истинно, если переменная a больше переменной b и ложно в противном случае. |
| a == b | Истинно, если переменная a равна переменной b и ложно в противном случае. |
| a <= b | Истинно, если переменная a меньше либо равна переменной b и ложно в противном случае. |
| a >= b | Истинно, если переменная a больше либо равна переменной b и ложно в противном случае. |
| a ~= b | Истинно, если переменная a не равна переменной b и ложно в противном случае. |






