- сила поверхностного натяжения,
где 
- длина контура ограничивающего поверхность жидкости;
или 
- коэффициент поверхностного натяжения,
где ΔЕ – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади ΔS поверхности этой пленки;
- формула Лапласа, выражающая давление р, создаваемое сферической поверхностью жидкости радиуса R;
- высота поднятия жидкости в капиллярной трубке;
; ε ׀׀= 
– закон Гука;
- закон линейного расширения твердых тел при нагревании;
- закон объёмного расширения жидкостей при нагревании.
Примеры решения задач.
Пример 1. Зависимость пройденного телом пути от времени задается уравнением 
. Найти расстояние, пройденное телом, скорость и ускорение тела через 2 с после начала движения.
Дано: Решение:
Для нахождения расстояния пройденного телом
t = 2 c подставляем в уравнение движения время
м
s =? Скорость в заданный момент времени
υ =? определяется как первая производная
а =? пройденного пути по времени
м/с
Ускорение в заданный момент времени определяется как первая производная скорости по времени
м/с2
Ответ: s = 24 м, υ = 38 м/с, а = 42 м/с2
Пример 2.Тело, брошенное вертикально вверх, вернулось на землю через 5 с. Какова была начальная скорость тела и на какую высоту оно поднялось?
Дано: Решение:
t = 5 c Уравнения для равноускоренного движения
h =? 
и 
υ0 =? Запишем эту систему уравнений для тела движущегося вверх: 
и 
где t1 - время движения тела вверх, h – высота, на которую поднялось тело,
υ = 0 – скорость тела в верхней точке.
Время движения тела вверх и вниз одинаково, значит 
с
Выражаем начальную скорость
м/с
Находим высоту подъема тела
м
Ответ: υ0 = 24,5 м/с, h =30,625 м.
Пример 3. На наклонную плоскость, образующую угол 60° с горизонтом, поставлен кубик. Коэффициент трения между кубиком и плоскостью 0,5. С каким ускорением будет соскальзывать кубик?
 |
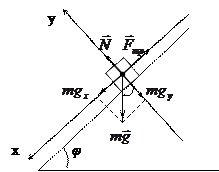Дано: Решение:
φ = 60°
μ = 0,5
а =?
Запишем уравнение движения кубика (2-й закон Ньютона) в векторной форме
Проекция этого уравнения на ось х будет иметь вид
,
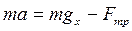где 
- проекция силы тяжести на ось х.
Проекция уравнения движения на ось у будет иметь вид
,
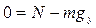где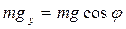 
- проекция силы тяжести на ось y.
Получившуюся систему уравнений дополним формулой силы трения
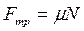
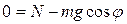отсюда 
Тогда сила трения будет равна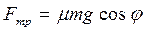 
Подставляем получившееся выражение в проекцию уравнения движения на ось Х
Находим ускорение
м/с
Ответ: а = 6 м/с
Пример 4. В закрытом сосуде находится 20 г азота и 32 г кислорода. Найти изменение внутренней энергии этой смеси газов при охлаждении её на 28К.
Решение: запишем формулу для нахождения изменение внутренней энергии смеси газов 
Молярную массу смеси газов найдем из закона Дальтона. 
, где
парциальное давление азота, 
- парциальное давление кислорода. Подставим эти значения в формулу закона Дальтона и выразим значение молярной массы смеси газов:
; 
Подставив численные значения, найдем, что 
Тогда удельная теплоемкость смеси газов при постоянном объеме равна-
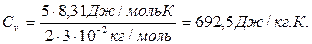
Найдем численное значение изменения внутренней энергии:
Ответ: 
Пример 5. Найти суммарное изменение энтропии при погружении 0,1 кг нагретого до 3000С железа в воду массой 1 кг при температуре 150С. Теплоемкости железа 470 Дж/ кг К, воды
4200 Дж/кг∙К
Решение: Изменение энтропии определяется
формулой
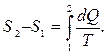
При остывании железа от Т1 до температуры θ выделяется количество теплоты равно: 
, тогда изменение энтропии железа равно
.
Температуру θ найдем, cоставив уравнение теплового баланса.
При остывании железа от Т1 до температуры θ выделяется количество теплоты равно: 
. При нагревании воды от Т2 до θ поглощается количество теплоты равное: 
. Т.к. Q1=Q2, то 
) = 
, отсюда найдем окончательную температуру воды θ = 291,15К.
Подставляя численные данные, получим:
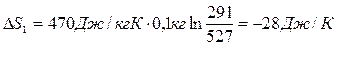
При нагревании воды от Т2 до температуры θ поглотится количество теплоты равно: 
, тогда изменение энтропии воды равно
.
Подставляя численные данные, получим:
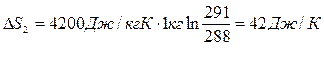
Суммарное изменение энтропии 
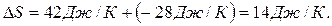
Ответ: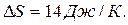 
Пример 6. На сколько нагреется капля ртути, полученная от слияния двух капель радиусом по 1 мм каждая?
Решение: Выделение энергии при слиянии капель ртути 
изменение площади поверхностного слоя равно 
, где r – радиус маленьких капель, R- радиус большой капли.
Радиус большой капли находим, приравнивая объем большой капли к сумме объемов слившихся капель: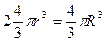 
, откуда 
. Тогда
.
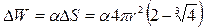- выделенная энергия пойдет на нагревание капли ртути, следовательно.
, отсюда
.
Подставив численные значения, получим:
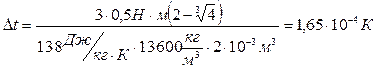
Ответ: 
К
