Механические колебания и волны.

Кинематика поступательного и вращательного движений.

– величина тангенциального (касательного) ускорения;

– величина нормального (центростремительного) ускорения;

– полное ускорение;

– модуль полного ускорения;

– угловая скорость;

– угловое ускорение;

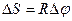; ; – связь линейных и угловых величин (путь, скорость и ускорение);

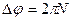– угловой путь;

– связь угловой скорости с частотой и периодом вращения.

Равнопеременное вращательное движение (ε=const):

– угловая координата;

; – угловой путь;

– угловая скорость.

 

Динамика. Работа, энергия. Законы сохранения.

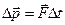; () – второй закон Ньютона;

– импульс тела;

– третий закон Ньютона;

– закон всемирного тяготения;

– сила тяжести;

– вес тела;

– сила упругости;

– сила трения;

– плотность тела;

– радиус-вектор центра масс.

Если , то – закон сохранения импульса;

; – работа силы;

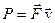; мощность;

– коэффициент полезного действия;

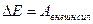; Е_{полн. 1}= Е_{полн. 2}+ А_{системы против внешних сил} – закон изменения полной энергии системы;

Е_{мех. 1}= Е_{мех. 2}+ А_{системы против внешних сил} + А_{системы против диссипативных сил} – закон изменения механической энергии;

– кинетическая энергия поступательного движения;

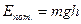– потенциальная энергия тела, поднятого над Землей на небольшую высоту (h << R _Земли);

– потенциальная энергия упруго деформированного тела; (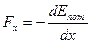) – связь потенциальной энергии и консервативной силы.

Если , то – закон сохранения полной энергии.

Если и отсутствуют диссипативные силы, то – закон сохранения механической энергии.

 

Динамика вращательного движения.

() – момент силы;

() – момент инерции тела;

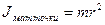– момент инерции материальной точки;

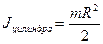; ; ; ; – моменты инерции тел относительно оси, проходящей через центр масс; – момент инерции стержня относительно оси, проходящей через его конец;

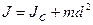– теорема Штейнера;

– закон динамики вращательного движения.

Динамика вращательного движения. Работа, энергия.

Законы сохранения энергии и момента импульса.

; – момент импульса тела;

() – закон динамики вращательного движения в импульсной форме (закон изменения момента импульса).

Если , то – закон сохранения момента импульса.

– работа при вращательном движении;

– кинетическая энергия вращательного движения.

 

Упругие свойства твердых тел.

ε _׀׀= – относительное удлинение;

– относительное поперечное сжатие;

() – нормальное (тангенциальное) механическое напряжение;

; ε _׀׀= – закон Гука;

/ ε _׀׀ – коэффициент Пуассона;

– закон Гука для деформации сдвига; где γ – деформация сдвига (угол сдвига);

– связь между модулем Юнга и модулем сдвига.

 

 

Механические колебания и волны.

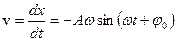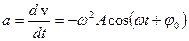; ; – смещение из положения равновесия, скорость и ускорение колеблющейся точки;

– дифференциальное уравнение гармонических колебаний;

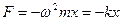– возвращающая сила при гармонических колебаниях;

; ; ; (здесь 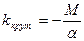– модуль кручения) – период колебаний пружинного, математического, физического и крутильного маятников;

; – закон сохранения энергии;

; – амплитуда и начальная фаза результирующего колебания при сложении однонаправленных колебаний одинаковой частоты;

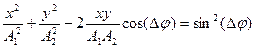– уравнение траектории точки, ; – амплитуда и начальная фаза результирующего колебания при сложении однонаправленных колебаний одинаковой частоты;

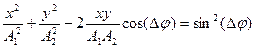– уравнение траектории точки, колеблющейся с одинаковыми частотами в перпендикулярных направлениях;

– дифференциальное уравнение затухающих колебаний;

– круговая частота собственных незатухающих колебаний;

– коэффициент затухания;

– сила сопротивления при затухающих колебаниях;

– уравнение затухающих колебаний;

– круговая частота затухающих колебаний;

– амплитуда затухающих колебаний;

– логарифмический декремент затухания;

– добротность;

– добротность;

(здесь ) – дифференциальное уравнение вынужденных колебаний;

; ; – смещение из положения равновесия, амплитуда и фаза вынужденных колебаний; 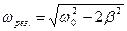– резонансная частота;

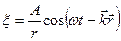, – уравнения плоской и сферической волн;

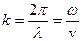– волновое число (волновой вектор);

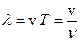– длина волны;

; – скорость распространения продольных и поперечных волн в твердом теле;

– скорость звука в газе;

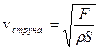– скорость распространения поперечной волны по струне.