В XIX веке авторитетные химики Томсен и Бертло полагали, что самопроизвольно протекают только экзотермические процессы. Опыт показывает, что существуют две тенденции для процесса в любой системе, в том числе и в химической. С одной стороны, система стремится снизить теплосодержание и перейти в более устойчивое состояние с минимальной энергией. Эту тенденцию характеризует изменениеэнтальпии. Согласно принципу самопроизвольности реакций (принцип Бертло) химические процессы идут самопроизвольно только при выделении теплоты. Это правило не противоречит первому началу термодинамики и действительно часто оправдывается на практике.
Однако критерий экзотермичности процесса не является универсальным и однозначным. Самопроизвольными могут быть и эндотермические реакции, идущие с поглощением тепла.
Если взять стаканчик с сухой солью (роданид аммония NH4 CNS или нитрат калия), поставить его на мокрую фанерку, налить немного воды и перемешать, то соль растворится с таким поглощением тепла, что стаканчик покроется инеем и примерзнет к фанерке. Кроме того, реакция, идущая в данных условиях (например, при данной температуре) с выделением тепла (прямая реакция), в других условиях (при другой температуре) идет с поглощением тепла (обратная реакция).
Вторая тенденция любого процесса –стремление перевести систему в наиболее вероятное состояние, когда частицы, составляющие систему, расположены наиболее беспорядочно. Например, процесс испарения воды Н2О(ж) →Н2О(п) идет самопроизвольно и при
T < T кип. Чем же объясняется такая возможность?
Вероятность состояния оценивается особой функцией состояния – энтропией (S).
Понятие энтропии
Чтобы это понять, рассмотрим ещё одну функцию состояния, которую ввел в термодинамику Р. Клаузиус (1850 г.) при анализе КПД тепловой машины.
Оказалось, что для обратимых тепловых процессов, протекающих при постоянной температуре, изменение некоторой величины S связано с количеством энергии, передаваемой в форме тепла ∆QT, следующим соотношением:
∆ S = ∆ QT /T.
Величина S является функцией состояния, поскольку, как оказалось, зависит только от природы и параметров системы T, р и V и не зависит от того, каким путем система приходит из начального состояние в конечное. Эта функция имеет размерность Дж/ К и называется энтропией.
В пределе соотношение, введенное Клаузиусом (и называемое формулой Клаузиуса) выглядит так:
dS = δ QT / T.
Формула Клаузиуса является определением термодинамической энтропии как функции состояния.
Энтропия – экстенсивная функция состояния, поэтому для удобства сравнения различных систем (а в химии системы различаются по составу) чаще используется удельная характеристика – энтропия одного моля вещества в системе, имеющая размерность Дж/(моль К).
Обратим внимание на то, что в правой части формулы Клаузиуса – строго фиксированная температура (температура – мера кинетической энергии частиц). А потому передаваемое здесь тепло не изменяет среднюю кинетическую энергию частиц в системе. Но что же тогда меняется?
Поскольку тепло – это та часть кинетической энергии частиц системы, которая связана исключительно с хаотическим движением,можно сказать, что понятие тепла выявляетособую качественную характеристику системы – её хаотичность, а энтропия – количественная мера хаотичности системы.
Осознание понятия термодинамической энтропии, количественно характеризующей хаос, утвердило и сам хаос как одно из объективных качеств окружающего нас физического мира,равнозначное таким его характеристикам, как энергия, масса, объем, давление.
К таким же выводам приводит и другой подход к определению энтропии, который развил Л. Больцман, исходя из вероятностного подхода к описанию термодинамических систем.
Больцман связал хаотичность с непредсказуемостью: чем более хаотична система, тем труднее предсказать ее конкретную структуру при заданном термодинамическом состоянии, т.е. при заданных параметрах. Например, для газов чрезвычайно сложно указать конкретные координаты и импульсы всех молекул в заданном объеме при определенных р, V, T. Он ввел и меру сложности предсказания – термодинамическую вероятность W.
Термодинамическая вероятность W – это число возможных микросостояний системы, которые обеспечивают параметры данного макросостояния.
Больцман показал, что такая, вероятностная, трактовка хаотичности связана с энтропией по Клаузиусу соотношением
S = k∙ ln W,
где k – постоянная Больцмана (1,38∙10- 23Дж/К), W – термодинамическая вероятность данного состояния.
Рассмотрим такой вопрос: сколькими способами (взаимным расположением в пространстве и заданием энергетического состояния) можно реализовать систему, содержащую 1 моль газообразного водорода при давлении 1,013∙105 Па и температуре 298 К?
Энтропия моля водорода при этих (стандартных) условиях равна S 0298 H 2 = 130,59 Дж/(моль К).
Расчет по формуле Больцмана дает
W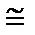 
exp (10000000000000000000000000).
Таково число вариантов размещения в 22,4 литрах пространства 6,02∙1023 штук молекул водорода при стандартных условиях. Очевидно, что это «стандартное состояние» весьма хаотично!
Расчет изменения энтропии в конкретных процессах является хорошо разработанным разделом термодинамики. После введения понятия энтропии оказалось, что в термодинамических системах, помимо первого, существует и действует второй закон (второе начало) термодинамики.
Он имеет много формулировок, первую из которых дал Клаузиус (теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому), однако для нас будет важна следующая:
в изолированных системах самопроизвольно протекают только процессы, сопровождающиеся увеличением энтропии.
Математически это записывается как
dS ad≥0 (здесь индекс ad – адиабатический процесс).
Равенство нулю dS ad возможно при обратимом проведении циклических (равновесных) процессов.
Следует подчеркнуть, что действие второго начала термодинамики строго ограничено только изолированными системами. А вот понятие энтропии, которое породило этот закон, применимо ко всем видам термодинамических систем и играет важную роль в понимании хода всех термодинамических процессов. Вне рамок адиабатических процессов энтропия, по физическому смыслу представляющая хаос, если в системе ей не противостоит какая-то противодействующая причина, стремится к возрастанию.
В общем случае для любого процесса второй закон термодинамики можно представить в виде
Знак равенства относится к равновесным процессам, знак неравенства – к неравновесным. Знак неравенства появляется потому, что работа, производимая системой в необратимом (неравновесном)
процессе, меньше работы, производимой в обратимом (равновес-
ном) процессе: W неравн< W равн. Из первого начала термодинамики
(dU =d Q + d W) и с учетом того, что внутренняя энергия – функция состояния (dU равн = dU неравн), следует: d Q неравн > d Q равн. Тогда для необратимого (неравновесого) процесса изменение энтропии
