МАТЕМАТИКА
Часть вторая
Учебно-методическое указание по изучению дисциплины и выполнению контрольных работ для студентов-заочников первого курса
высшего профессионального образования
21.03.01(131000). 13.03.02(140400),
Краснодар
УДК
Составители: доцент Терещенко И.В., доцент Братчиков А.В., ассистент Егорова Л.В.
Математика. Учебно – методические указания по изучению дисциплины и выполнению контрольных работ для студентов-заочников специальностей140211,140101,130503 факультета НГиЭ высшего профессионального образования. – Краснодар 2005. – 37 с.
В учебно-методических указаниях изложены программа дисциплины, варианты контрольных заданий, темы практических занятий, вопросы к зачету (или экзамену), рекомендуемая литература, приведены примеры выполнения и требования к оформлению контрольных работ.
Печатается по решению методического совета Кубанского государственного технологического университета.
Рецензенты: д-р техн. наук, профессор Вартумян Г.Т.
канд. техн. наук, доцент Данович Л.М.
© КубГТУ, 2005
Содержание
Введение. 3
1. Инструкция по работе с учебно–методическими указаниями. 3
2. Программа дисциплины. 4
3. Контрольные работы. 5
4. Задания на контрольную работу. 13
5 Содержание и оформление контрольных работ. 19
6 Темы практических занятий. 19
7. Вопросы для подготовки к экзамену (зачету) 20
8. Список рекомендуемой литературы.. 21
Введение
Инженер должен в области математики иметь представление:
- о математике как особом способе познания мира, общности ее понятий и
представлений;
- о математическом моделировании;
- об информации, методах ее хранения, разработки и передачи;
знать и уметь использовать:
- основные понятия и методы математического анализа, аналитической геометрии, линейной алгебры, теории функций комплексного переменного, теории вероятностей и математической статистики, дискретной математики;
- математические модели простейших систем и процессов в естествознании и технике;
- вероятностные модели для конкретных процессов и проводить расчеты в рамках построенной модели;
иметь опыт:
- употребления математической символики для выражения количественных и качественных отношений объектов;
- исследования моделей с учетом их иерархической структуры и оценки пределов применимости полученных результатов:
- использования основных приемов обработки экспериментальных данных;
- аналитического и численного решения алгебраических уравнений;
- исследования, аналитического и численного решения обыкновенных дифференциальных уравнений;
- аналитического и численного решения основных уравнений математической физики;
- программирования и использования возможностей вычислительной техники и программного обеспечения;
Цель курса «Математика»:
- дать студентам необходимую математическую подготовку для изучения общенаучных, общеинженерных и специальных дисциплин;
- привить студентам навыки логического и алгоритмического мышления;
- овладеть методами исследования и решения математических и прикладных задач по специальности;
- выработать умения самостоятельно расширять математические знания и применять их при анализе инженерных задач.
Инструкция по работе с учебно–методическими указаниями.
В разделе «Программа дисциплины» приведены темы и указывается, что необходимо знать в пределах каждой темы. В конце тем приводятся вопросы для самопроверки и литература из списка рекомендуемой литературы с указанием глав, страниц, где излагается материал темы.
Пример.
Литература: [2, гл.2 c. 3-9], [4, c. 143-162],
где 2 и 4 – порядковые номера литературных источников из списка рекомендуемой литературы.
Вариант контрольного задания выбирается по последней цифре шифра зачётной книжки. Последняя цифра шифра (0) соответствует 10 варианту в контрольном задании.Например, в 10 варианте выполняют следующие номера из предложенных заданий контрольной работы: 210,220,230 и так далее.
В разделе «Темы практических занятий» приводятся наименования практических занятий, которые будут проводиться в период экзаменационной сессии, и указывается литература для подготовки.
Программа дисциплины.
Тема 6. Функции нескольких переменных.
Функции многих переменных, их область определения. Частные производные. Наибольшее и наименьшее значения функции. Производная по направлению. Градиент. Метод наименьших квадратов.
Литература: [3, гл12 c. 284 – 304]
Вопросы для самоконтроля.
1. Вычисление частных производных функции многих переменных.
2. Вычисление производной по направлению.
3. Нахождение наибольшего и наименьшего значений функции.
4. Решение задач с помощью метода наименьших квадратов.
Тема 7 .Интегральное исчисление.
Неопределенный интеграл. Приближенное значение определенного интеграла. Несобственные интегралы. Приложения определенного интеграла.
Литература: [3, гл7,8 с. 159-215].
Вопросы для самоконтроля.
1. Вычисление неопределенных интегралов..
2. Вычисление приближенного значения интеграла 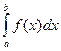 с помощью формулы Симпсона.
с помощью формулы Симпсона.
3. Вычисление несобственных интегралов первого и второго рода.
4. Определенный интеграл и его приложения.
Тема 8. Обыкновенные дифференциальные уравнения.
Дифференциальные уравнения первого порядка. Уравнение Бернулли. Дифференциальные уравнения высших порядков. Системыдифференциальных уравнений.
Литература:[3, гл15 с. 416-449].
Вопросы для самоконтроля.
1. Решение уравнений с разделяющимися переменными..
2. Линейные дифференциальные уравнения первого и второго порядка..
3. Дифференциальные уравнения, не содержащие искомой функции.
4. Дифференциальные уравнения, не содержащие независимой переменной.
5. Решения систем дифференциальных уравнений.
Контрольные работы.
Программой дисциплины «Математика» для студентов I курса предусмотрено выполнение контрольных работ №3.
3.1. При выполнении контрольной работы №3 необходимо изучить функции многих переменных, интегральные исчисления и теорию обыкновенных дифференциальных уравнений. Ниже приведены примеры выполнения расчетов.
К заданиям 201-210.
Пример. Проверить, что  для функции
для функции  .
.
Решение. Находим частные производные второго порядка.

Получим тождество:
 =
= 
К заданиям 211-220. Н айти наибольшее и наименьшее значения функции  в круге
в круге 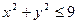
Решение: Для нахождения наибольшего и наименьшего значений функции в замкнутой области необходимо:
- Найти критические точки (лежащие внутри данной области) и вычислить в них значения функции.
- Найти наибольшее (наименьшее) значения функции на границе области.
- Сравнить все полученные значения функции.
Данная функция имеет частные производные: 


 - критическая точка
- критическая точка

Границей данной области является окружность 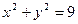 или
или  , где
, где  . Функция
. Функция  на границе области становится функцией одной переменной
на границе области становится функцией одной переменной  :
:
 , аргумент которой изменяется на отрезке
, аргумент которой изменяется на отрезке 
Найдем наибольшее и наименьшее значения функции 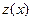 на указанном отрезке
на указанном отрезке 

Вычисляем ее значения на концах отрезка  , т.е. в точках
, т.е. в точках 
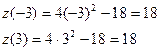
Сравнивая значение, заключаем, что функция  имеет наибольшее значение, равное 18 и наименьшее значение, равное -18, причем
имеет наибольшее значение, равное 18 и наименьшее значение, равное -18, причем

К заданиям 221-230.
Пример.Даны функция 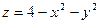 , точка
, точка  и вектор
и вектор 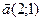 , найти:
, найти:
а)  в точке А;
в точке А;
б) производную в точке А по направлению вектора 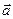 .
.
Решение:
а) Имеем 
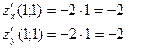
Значит, 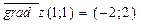
б)Найдем направляющие косинусы вектора 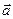 ,
, 

Следовательно, 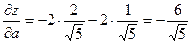
К заданиям 231-240.
Дана система точек, координаты которых указаны в таблице, число точек n=6

Требуется методом наименьших квадратов найти функцию  так, чтобы она отличалась как можно меньше от данной системы точек. Неизвестные коэффициенты находим из системы:
так, чтобы она отличалась как можно меньше от данной системы точек. Неизвестные коэффициенты находим из системы:

где 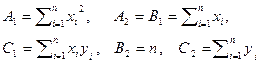
В нашем случае система имеет вид 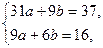
Решим ее методом определителей:

Искомое уравнение 
К заданиям 241-250.
Пример. Найти неопределенные интегралы.
а) 
Подстановка 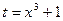 . Тогда
. Тогда  , откуда
, откуда  .
.
Таким образом, 
б) 
Применяем формулу интегрирования по частям 
Пусть 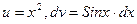 , тогда
, тогда 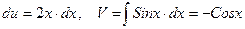
Получаем 
К интегралу в правой части снова применяем формулу интегрирования по частям.
Пусть
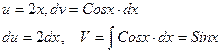
Таким образом, 
в) 
Подынтегральная функция является правильной рациональной дробью, знаменатель которой 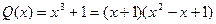
Подынтегральную функцию разложим на дроби
 , откуда
, откуда
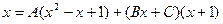
Раскроем скобки в правой части и приведем подобные:

Приравнивая соответствующие коэффициенты при  в левой и правой частях последнего равенства получим систему трех уравнений:
в левой и правой частях последнего равенства получим систему трех уравнений:

Таким образом, 

Решим отдельно интеграл
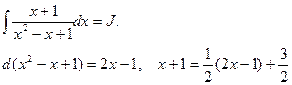

Итак,

г) 
Наименьшее общее кратное показателей корней равно 6, поэтому делаем подстановку
 ,
,  , то есть
, то есть

К заданиям 251-260. Пример. Вычислить приближенное значение интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 8 равных частей. Все вычисление производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 8 равных частей. Все вычисление производить с округлением до третьего десятичного знака.
Решение: Делим интервал [1;9] на 8 равных частей, находим длину одной части
h=  ,
,
точки деления  значения
значения  подынтегральной функции
подынтегральной функции 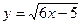
В этих точках:

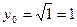 ё
ё





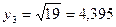
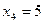


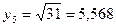






По формуле Симпсона
 .
.
К заданиям 261-270
Пример. Вычислить несобственный интеграл или доказать его расходимость.

Решение: Подынтегральная функция терпит разрыв при х=3 
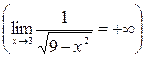
Согласно формуле 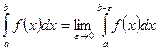
Имеем 
Интеграл сходится и его величина составляет  .
.
К заданиям 271 ‑ 280.
Пример. Вычислить длину дуги полукубической параболы  между точками А(2;1) и B(5;-8).
между точками А(2;1) и B(5;-8).
Решение:
Длина дуги АВ определяется формулой 
Разрешаем данное уравнение относительно y и находим  :
:

Подставляя в формулу, находим

К заданиям 281 ‑300.
Пример. Найти общее решение дифференциального уравнения.
Преобразуем уравнение к виду 

Сделав подстановку  ,т.е. y = u x,
,т.е. y = u x,
Получим  или
или 
Интегрируя, имеем:
 , т.е.
, т.е. 
Отсюда  , т.е.
, т.е. 
Учитывая, что  , получаем общее решение заданного уравнения
, получаем общее решение заданного уравнения

2. 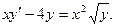
Уравнение приводится к виду  ,где
,где
 - непрерывные функции.
- непрерывные функции.
Это уравнение Бернулли 
Полагаем  . Получаем
. Получаем
 или
или 
Решаем первое уравнение  ,
,
Разделяя переменные  , т.е.
, т.е. 
Выбирая простейшие решения (С=0), находим 
Решаем второе уравнение
 , где
, где  или
или
 , т.е.
, т.е.  , откуда
, откуда

Таким образом,  , где
, где 
 - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
3. 
Положим y`=p=p(y). Тогда  , а исходное уравнение примет вид:
, а исходное уравнение примет вид:

Т.е.  , откуда
, откуда

Заменим p на y`, получим 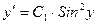
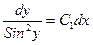 , или
, или 
Получим общее решение исходного уравнения в неявном виде.
К заданиям 301-310.
Пример. Найти общее решение дифференциального уравнения 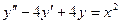
А) Найдем  , решим соответствующее однородное уравнение
, решим соответствующее однородное уравнение  , составим
, составим
характеристическое уравнение:

Тогда  - общее решение однородного уравнения.
- общее решение однородного уравнения.
Б) Найдем у - частное решение неоднородного уравнения. Его будем искать в виде, подобном первой части. Там  - это многочлен второй степени, в общем виде это
- это многочлен второй степени, в общем виде это
 , т.е.
, т.е.  . Так как
. Так как  есть решение первоначального дифференциального уравнения, то оно обращает это уравнение в тождество. Найдем
есть решение первоначального дифференциального уравнения, то оно обращает это уравнение в тождество. Найдем
 и подставим в первоначальное уравнение
и подставим в первоначальное уравнение

Два многочлена равны, когда равны их коэффициенты при одинаковых степенях неизвестных. Приравняем коэффициенты  в обеих частях
в обеих частях

Тогда 
Общее решение 
К заданиям 311-320.
Дана система линейных уравнений:
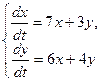
Найти общее решение систем с помощью характеристического уравнения
Решение: Составим характеристическое уравнение  , где
, где
 - матрица системы,
- матрица системы,
 - единичная матрица.
- единичная матрица.
Имеем 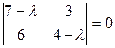 , или
, или 
Его корни 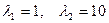 - характеристические числа матрицы.
- характеристические числа матрицы.
При  уравнения для определения собственного вектора имеют вид
уравнения для определения собственного вектора имеют вид  и
и
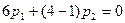 и сводятся к одному уравнению
и сводятся к одному уравнению  . Последнее определяет вектор (1;-2).
. Последнее определяет вектор (1;-2).
При  получаем уравнения
получаем уравнения  или
или 
Это уравнение определяет вектор (1;1). Поучаем фундаментальную систему решений:
Для  :
: 
Для  :
: 
Общее решение системы имеет вид:

К заданиям 321-330.
У какой кривой отрезок любой касательной, заключенный между точкой касания и осью абсцисс, делится осью ординат пополам?
Решение: Уравнение касательной в любой точке (x; y) искомой кривой будет  , где
, где  - координаты любой точки на касательной.
- координаты любой точки на касательной.
Полагая в этом уравнении  , найдем абсциссу
, найдем абсциссу  точки пересечения касательной с осью Ох:
точки пересечения касательной с осью Ох: 
Решая это дифференциальное уравнение искомой кривой как уравнение с разделяющимися переменными, получим 

Следовательно, искомая кривая есть парабола с вершиной в начале координат, симметричная относительно оси Ох.
Задания на контрольную работу.
Контрольная работа №3
Задание 1. Дана функция z=f(x;y). Показать, что F(x; y; z;  )
)  .
.
№201.  ,
, 
№202. 

№203.  ,
, 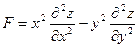
№204.  ,
, 
№205.  ,
, 
№206.  ,
, 
№207.  ,
, 
№208.  ,
, 
№209.  ,
, 
№210.  ,
, 
Задание 2. Найти наименьшее и наибольшее значения функции  в замкнутой области D, заданной системой неравенств. Сделать чертеж.
в замкнутой области D, заданной системой неравенств. Сделать чертеж.
№211.  ;
; 
№212.  ;
; 

№213. 
 ,
, 
№214. 


№215.  ;
; 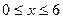 ,
, 
№216. 
 ,
, 
№217. 
 ,
, 
№218. 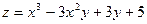 ;
; 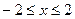 ,
, 
№219.  ;
;  ,
, 
№220.  ;
;  ,
, 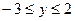
Задание 3. Даны функция  , точка
, точка  и вектор
и вектор 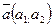 .
.
Найти: 1)  в точке A; 2) производную в точке A по направлению вектора
в точке A; 2) производную в точке A по направлению вектора 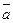 .
.
№221.  , A(1;1);
, A(1;1); 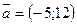
№222.  , A(-1;2);
, A(-1;2); 
№223.  , A(1;3);
, A(1;3); 
№224.  A(1;1);
A(1;1); 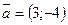
№225.  A(2;-1);
A(2;-1); 
№226.  A(1;2);
A(1;2); 
№227.  A(4;-3);
A(4;-3); 
№228.  A(-1;-2);
A(-1;-2); 
№229.  , A(-5;6);
, A(-5;6); 
№230.  A(2;3);
A(2;3); 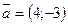
Задание 4. Экспериментально получены пять значений функции  при пять значениях аргумента, которые записаны в таблице:
при пять значениях аргумента, которые записаны в таблице:
| x | |||||
| y | y1 | y2 | y3 | y4 | y5 |
Методом наименьших квадратов найти функцию вида  , выражающую приближенную (аппроксимирующую) функцию
, выражающую приближенную (аппроксимирующую) функцию  . Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции
. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции  .
.
№231. y|| 3,4 | 3,5 | 3,1 | 1,2 | 2,4 |
№232. y|| 0,6 | 1,6 | 3,7 | 5,2 | 6,4 |
№233. y|| 4,7 | 5,5 | 4,0 | 2,1 | 2,7 |
№234. y|| 4,8 | 5,3 | 4,2 | 3,8 | 2,3 |
№235. y|| 3,9 | 5,1 | 3,3 | 1,5 | 2,3 |
№236. y|| 5,7 | 6,7 | 4,9 | 3,4 | 3,9 |
№237. y|| 5,2 | 6,3 | 4,8 | 2,7 | 1,8 |
№238. y|| 5,1 | 4,8 | 5,2 | 2,9 | 2,1 |
№239. y|| 4,5 | 2,5 | 0,5 | 3,5 | 1,6 |
№240. y|| 3,6 | 4,5 | 3,2 | 1,3 | 1,8 |
Задание 5. Найти неопределенные интегралы. В п. а) и б) результаты проверить дифференцированием.
№241. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
№242. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
№243. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
№244. а) 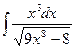 ; б)
; б)  ; в)
; в) 
 г)
г) 
№245. а)  б)
б) 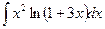 ; в)
; в)  ; г)
; г)  .
.
№246. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
№247. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
№248. а) 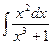 ; б)
; б)  ; в)
; в) 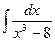 ; г)
; г)  ;
;
№249. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
№250. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Задание 6. Вычислить приближенные значения определенного интеграла 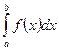 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 равных частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 равных частей. Все вычисления производить с округлением до третьего десятичного знака.
№251.  №255.
№255. 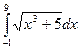 №259.
№259. 
№252.  №256.
№256.  №260.
№260. 
№253.  №257.
№257. 
№254.  №258.
№258. 
Задание 7. Вычислить несобственный интеграл или доказать его расходимость.
№261.  №266.
№266. 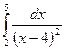
№262.  №267.
№267. 
№263.  №268.
№268. 
№264. 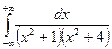 №269.
№269. 
№265.  №270.
№270. 
Задание 8.
№271. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций 
 вокруг оси Oy.
вокруг оси Oy.
№272. Вычислить длину дуги кривой  от точки
от точки  до точки
до точки  .
.
№273. Вычислить площадь фигуры, ограниченно линиями, заданными уравнениями  ,
,  .
.
№274. Вычислить площадь фигуры, ограниченной кардиоидой  .
.
№275. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций  ,
,  вокруг оси Ox.
вокруг оси Ox.
№276. Найти площадь фигуры, ограниченной линиями  ,
, 
№277. Найти площадь фигуры, ограниченной астроидой  ,
, 
№278. Вычислить длину дуги кривой 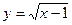 от точки А(1;0) до точки B(2;1).
от точки А(1;0) до точки B(2;1).
№279. Найти объем тела, образованного вращением фигуры, ограниченной линиями 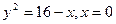 вокруг оси Oy.
вокруг оси Oy.
№280. Найти объем тела, образованного вращением фигуры, ограниченной линиями  ,
, 
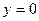 вокруг оси Oy.
вокруг оси Oy.
Задание № 9. Найти общее решение дифференциального уравнения.
№ 281. 

№ 282. (1+ x  )
)  - 2 xy= (1+ x
- 2 xy= (1+ x  )
) 
№ 283.  =
= 
№ 284. x  = y ln (
= y ln ( )
)
№ 285. x  + x tg
+ x tg 
№ 286.  + y cos = sin 2x
+ y cos = sin 2x
№ 287.  + 2xy = 2xy
+ 2xy = 2xy 
№ 288. 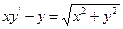
№ 289. x  + y = 4x
+ y = 4x 
№ 290.  - y=
- y= 

Задание 10. Найти общее решение дифференциального уравнения.
№291. (1- x 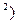
 x
x 
№ 292. 
 (1+ (
(1+ ( )
) 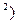
№ 293. 1+(  )
) 
№ 294. x 


№ 295. 

№296. 
№297. 
№298. 
№299. 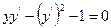
№300. 

Задание 11. Найти частное решение дифференциального уравнения  , удовлетворяющее условиям
, удовлетворяющее условиям  ,
,  .
.
№301. 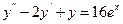 ,
, 

№302.  ,
, 

№303.  ,
, 

№304.  y (0) =0,
y (0) =0, 

№305.  , y (0)= 1,
, y (0)= 1, 
№306.  y (0) =0,
y (0) =0, 

№307. 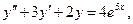 y (0) = 1,
y (0) = 1, 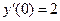
№308. 


№309. 


№310. 


Задание 12. Дана система линейных дифференциальных уравнений с постоянными коэффициентами
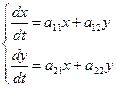
Требуется: 1) Найти общее решение системы с помощью характеристического уравнения;
2) записать данную систему и её решение в матричной форме.
№311.

№312.

№313.

№314.

№315.


№316.

№317.

№318.

№319.

№320.

Задание 13.
№321. Пуля, двигаясь со скоростью  м/с, ударяется о достаточно плотную стену и начинает углубляться в нее, испытывая силу сопротивления стены; эта сила сообщает пуле отрицательное ускорение, пропорциональное квадрату её скорости с коэффициентом пропорциональности
м/с, ударяется о достаточно плотную стену и начинает углубляться в нее, испытывая силу сопротивления стены; эта сила сообщает пуле отрицательное ускорение, пропорциональное квадрату её скорости с коэффициентом пропорциональности 
 . Найти скорость пули через 0,001 с после вхождения пули в стену.
. Найти скорость пули через 0,001 с после вхождения пули в стену.
№322. Материальная точка массой 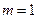 г движется прямолинейно. На нее действует сила в направлении движения, пропорциональная времени с коэффициентом пропорциональности
г движется прямолинейно. На нее действует сила в направлении движения, пропорциональная времени с коэффициентом пропорциональности 
 , и сила сопротивления среды, пропорциональная скорости с коэффициентом пропорциональности
, и сила сопротивления среды, пропорциональная скорости с коэффициентом пропорциональности 
 . Найти скорость точки через 3 секунды после начала движения, если начальная скорость точки была равна нулю.
. Найти скорость точки через 3 секунды после начала движения, если начальная скорость точки была равна нулю.
№323. В сосуде 100 л водного раствора соли. В сосуд втекает чистая вода со скоростью 
 , а смесь вытекает с той же скоростью, причем перемешивание обеспечивает равномерную концентрацию раствора. В начальный момент в растворе содержалось
, а смесь вытекает с той же скоростью, причем перемешивание обеспечивает равномерную концентрацию раствора. В начальный момент в растворе содержалось  кг соли. Сколько соли будет содержаться в сосуде через 20 мин после начала процесса?
кг соли. Сколько соли будет содержаться в сосуде через 20 мин после начала процесса?
№324. Кривая проходит через точку A(2;1) и обладает тем свойством, что угловой коэффициент касательной в любой её точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности  . Найти уравнение кривой.
. Найти уравнение кривой.
№325. Материальная точка массой 
 г погружается в жидкость, сила сопротивления которой пропорциональна скорости погружения с коэффициентом пропорциональности
г погружается в жидкость, сила сопротивления которой пропорциональна скорости погружения с коэффициентом пропорциональности 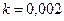 кг/с. Найти скорость точки через 1с после начала погружения, если в начальный момент она была равна нулю.
кг/с. Найти скорость точки через 1с после начала погружения, если в начальный момент она была равна нулю.
№326. Моторная лодка двигалась в спокойной воде со скоростью  кг/ч. На полном ходу её мотор был выключен и через 10 секунд скорость лодки уменьшилась до
кг/ч. На полном ходу её мотор был выключен и через 10 секунд скорость лодки уменьшилась до  км/ч. Сила сопротивления воды пропорциональна скорости движения лодки. Найти скорость лодки через 1 минуту после остановки мотора.
км/ч. Сила сопротивления воды пропорциональна скорости движения лодки. Найти скорость лодки через 1 минуту после остановки мотора.
№327. Кривая проходит через точку А(1;2) и обладает тем свойством, что отношение ординаты любой ее точки к абсциссе пропорционально угловому коэффициенту касательной к этой точки, проведённой в этой же точке, с коэффициентом пропорциональности  . Найти уравнение кривой.
. Найти уравнение кривой.
№328. Кривая проходит через точку A(1;2) и обладает тем свойством, что произведение углового коэффициента касательной в любой её точке на сумму координат точки касания равно удвоенной ординате этой точки. Найти уравнение кривой.
№329. Кривая проходит через точку А(2;4) и обладает тем свойством, что отрезок, отсекаемый на оси абсцисс касательной, проведенной в любой точке кривой, равен кубу абсциссы точки касания. Найти уравнение кривой.
№330. Кривая проходит через точку А(1;5) и обладает свойством, что отрезок, отсекаемый на оси ординат любой касательной, равен утроенной абсциссе точки касания. Найти уравнение кривой.
Содержание и оформление контрольных работ
4.1. Требования к оформлению контрольной работы: в случае рукописного варианта контрольная работа выполняется в тетради (12л.) на обложке необходимо указать № к.р., свой факультет, специальность, ши







