| EA, B | T, c | L, мГн | С1, мкФ | С2, мкФ | R1, Ом | Определить |
| 0,015 | 35,76 | 210,9 | 137, 84 | 17,32 | u bc |
1. Трёхфазный генератор, создаёт трёхфазную симметричную систему синусоидальных фазных ЭДС прямой последовательности. В комплексной форме система фазных ЭДС (напряжений) трёхфазного симметричного генератора запишется:
Cистема линейных напряжений источника:
К трёхфазному симметричному источнику энергии подключена симметричная нагрузка, соединённая « звездой » при наличии сопротивлений в линейных проводах.
Реактивные сопротивления индуктивности и ёмкостей токам заданной частоты определятся:
;
Ом;
Ом;
Ом.
Комплексное сопротивление в линейных проводах:
Комплексное сопротивление фазы симметричной нагрузки:
Расчётная схема трёхфазной цепи приведена на рисунке 2.22.
Рисунок 2.22 – Расчётная схема трёхфазной цепи
Комплексное сопротивление одной фазы трёхфазной цепи:
Схема трёхфазной цепи (рисунок 2.22) представляет собой симметричную трёхфазную цепь, для которой потенциалы нулевых точек источника и нагрузки равны: 
. Расчёт такой электрической цепи ведётся по расчётной схеме для одной фазы, приведённой ниже:
Линейные токи симметричной трёхфазной цепи определятся:
Токи в активных сопротивлениях и ёмкостях линии:
2. Комплексное действующее значение напряжения между заданными точками определится по закону напряжений Кирхгофа:
Мгновенное значение напряжения между заданными точками (закон изменения во времени):
.
3. Активная мощность симметричной трёхфазной цепи:
.
Или 
.
4. Для построения топографической векторной диаграммы находим комплексные действующие значения напряжений на всех участках трёхфазной электрической цепи (рисунок 2.22).
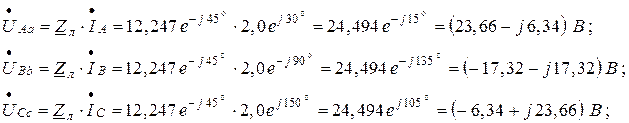Комплексные потенциалы точек схемы при условии, что за нулевой потенциал принят потенциал нулевой точки генератора:
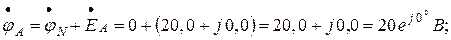
Задаёмся комплексной плоскостью и в масштабе тока 
строим векторы токов (рисунок 2.23). Выбираем масштаб напряжений (потенциалов) 
и в этом масштабе строим на комплексной плоскости векторы напряжений (потенциалов точек схемы).
Рисунок 2.23 – Векторная диаграмма токов и топографическая диаграмма напряжений трёхфазной цепи
Методические указания к решению задачи 3
С учётом индивидуального варианта задачи (№19 из таблицы 3.1) схема заданной электрической цепи с учётом сопротивления нагрузки Rн имеет вид, приведённый на рисунке 3.13.
| Вариант задачи | Рисунок схемы | Рисунок графика u1(t) | L, мГн | C, мкФ | Т, мс | Rн, Ом | Um, В |
| 3-4 | 2-2 | 5,8 |
Рисунок 3.13 – Схема электрической цепи
На входных зажимах электрической цепи действует периодическое несинусоидальное напряжение, показанное на рисунке 3.14.
Рисунок 3.14 – Напряжение на входе электрической цепи
1. Кривую заданного входного напряжения представим в виде тригонометрического ряда Фурье. В общем случае ряд Фурье для периодической несинусоидальной функции времени заданного входного напряжения запишется:
.
Определение составляющих ряда Фурье входного напряжения выполним, воспользовавшись табличными разложениями, при -
ведёнными в учебниках по теоретическим основам электротехники.
Прежде всего, выделяем во входном напряжении u1(t) постоянную составляющую:
.
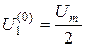Проводим новую ось времени на высоте постоянной составляющей напряжения 
. Для оставшейся части напряжения находим в учебниках и справочниках подобное табличное разложение. Затем определяем соотношения, учитывающие соответствие табличной кривой и заданного напряжения на входе электрической цепи, а также возможное их смещение по оси времени (опережение или запаздывание).
Для заданного входного напряжения подобная табличная кривая [Л.1 – приложение 1; Л.2 – таблица 7.1] имеет вид, приведённый на рисунке 3.15.
Рисунок 3.15 – Табличная кривая
Разложение в ряд Фурье табличной кривой:
.
Из сравнения заданного несинусоидального входного напряжения (рисунок 3.14) c табличной кривой (рисунок 3.15) имеем:
1) наличие постоянной составляющей 
;
2) 
;
3) 
;
4) напряжение на входе цепи опережает во времени табличную кривую на время t0:
.
Таким образом, заданное входное напряжение с учётом постоянной составляющей имеет следующее разложение в ряд Фурье:
С учётом заданных численных значений варианта задачи получаем следующий закон изменения напряжения на входе цепи:
График входного напряжения как сумма четырёх первых гармоник разложения имеет вид, представленный на рисунке 3.16.
Рисунок 3.16 – График входного напряжения как сумма гармоник
Обозначим сопротивления элементов схемы в общем виде как Rн,, и получим формулу для комплексной амплитуды напряжения на нагрузке через амплитуду входного напряжения. Полученное выражение пригодно для каждой гармоники, понимая под и сопротивления индуктивности и ёмкости для гармоники с номером.
Расчётная схема для произвольной гармоники “к” в комплексной форме имеет вид, представленный на рисунке 3.17.
Рисунок 3.17 – Расчётная схема для гармоники “к”
По законам Кирхгофа и Ома в комплексной форме для действующих значений электрическая цепь опишется уравнениями:
Выразим из уравнения (2) ток 
и подставим полученное значение в уравнение (3):
Полученное выражение для тока 
(6) подставим в уравнение (1), а затем выполним подстановку (4):
Искомая формула для комплексной амплитуды напряжения на нагрузке 
через амплитуду входного напряжения 
:
3. Используя полученную формулу, определим комплексную амплитуду напряжения на выходе цепи для нулевой (к = 0), первой (к = 1) и третьей (к = 3) гармоник (для схемы № 3-4).
1) Расчёт нулевой гармоники (к = 0).
Так как при постоянных токах и напряжениях в электрической цепи индуктивность представляет собой “ закоротку ” 
, а ёмкость представляет собой “ разрыв ветви ” 
, то для заданной цепи напряжение на нагрузке определится:
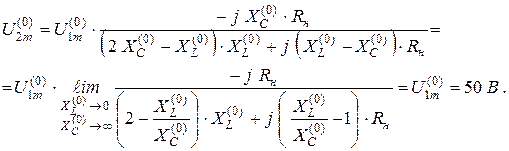
2) Расчёт первой гармоники (к = 1).
Частота основной (первой) гармоники сигнала:
Комплексное значение амплитуды входного напряжения:
.
Реактивные сопротивления индуктивностей и ёмкости при частоте первой гармоники напряжения на входе цепи:
Комплексная амплитуда напряжения на нагрузке:
3) Расчёт третьей гармоники (к = 3).
Комплексное амплитудное значение входного напряжения:
.
Реактивные сопротивления индуктивностей и ёмкости:
Комплексная амплитуда напряжения на нагрузке:
4) Расчёт пятой гармоники (к = 5).
Комплексное амплитудное значение входного напряжения:
.
Реактивные сопротивления индуктивностей и ёмкости:
Комплексная амплитуда напряжения на нагрузке:
4. Закон изменения во времени напряжения на нагрузке в виде ряда Фурье (мгновенное значение напряжения на выходе цепи):
5. Линейчатые спектры амплитуд входного напряжения 
и выходного напряжения 
– рисунок 3.18.
Рисунок 3.18 – Линейчатые спектры амплитуд входного (u1) и выходного (u2) напряжений
8. Закон изменения напряжения на нагрузке в функции времени приведён на рисунке 3.19.
Рисунок 3.19 – График изменения напряжения на нагрузке
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Зевеке Г.В. Основы теории цепей: учебник для вузов / Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.
2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: учебник для вузов / Л.А. Бессонов. – 10-е изд. – М.: Гардарики, 2001. – 638 с.
3. Попов В.П. Основы теории цепей: учебник для вузов / В.П. Попов. – 5-е изд., стер. – М.: Высшая школа, 2005. – 575 с.
4. Шебес М.Р. Задачник по теории линейных электрических цепей: учебное пособие для вузов / М.Р. Шебес, М.В. Каблукова. – 4-е изд., перераб. и доп. – М.: Высшая школа, 1990, – 544 с.
5. Бессонов Л.А. Сборник задач по теоретическим основам электротехники. / Л.А. Бессонов, И.Г. Демидова, М.Е. Заруди и др. – М.: Высшая школа, 1988, – 543с.
Учебное издание
Составители:
Князев Валерий Семёнович
Кипервассер Михаил Вениаминович
РАСЧЁТ УСТАНОВИВШИХСЯ ПРОЦЕССОВ
В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Методические указания к выполнению
расчётно-графических работ для студентов
электротехнических специальностей заочного обучения
по дисциплине «Теоретические основы электротехники»
Редактор Ю.А. Колокольцева
Подписано в печать 23.11 10г.
Формат бумаги 60´84 1/16. Бумага писчая. Печать офсетная.
Усл. печ. л. 2,70. Уч.- изд. л. 2,94. Тираж 100 экз. Заказ 919.
Сибирский государственный индустриальный университет.
654007, г. Новокузнецк, ул. Кирова, 42.
Издательский центр СибГИУ.
