Вступление
В математике изучают не только отношения, но и различные операции. Например, сложение, вычитание, умножение, деление, извлечение из корня - это операции над числами; пересечение, объединение, вычитание, декартово умножение - это операции над множествами; конъюнкция, дизъюнкция, отрицание - это операции над высказываниями и высказывательными формами. Операции над высказываниями и множествами появились в математике в XIX веке. Операции над высказываниями ввел английский математик Дж. Буль, а операции над множествами немецкий математик Г. Кантор. Оказалось, что операции над высказываниями и множествами обладают свойствами, аналогичными свойствам сложения и умножения чисел, но некоторые их свойства отличаются от свойств операций над числами.
Вообще в XIX веке в математике возникли разные ветви алгебры: обычных чисел, высказываний, множеств и другие. Каждая из них имела свои правила, но для некоторых видов алгебр эти правила были похожими. Стремление выяснить, что представляет собой любая операция, способствовало появлению общего понятия алгебраической операции.
Изучение свойств алгебраических операций привело математиков к выводу о том, что основная задача алгебры - изучение свойств операций, рассматриваемых независимо от объектов, к которым они применяются. И если первоначально алгебра была учением о решении уравнений, то в XX веке она превратилась в науку об операциях и их свойствах.
Учитель начальных классов первым знакомит детей с различными операциями над числами и их свойствами. Иногда в начальном курсе математики начинается изучение операций над множествами и предложениями. И естественно, чтобы грамотно обучать детей, видеть перспективу развития алгебраических понятий в дальнейшем обучении школьников математике, учителю необходимо знать, что такое алгебраическая операция, какими свойствами она может обладать, где и как она применяется.
Понятие алгебраической операции
Рассмотрим, например, хорошо известное нам сложение натуральных чисел. Выполняя эту операцию, мы, имея два числа, находим третье - сумму первых двух чисел. Так, складывая числа 5 и 9, получаем число 14, которое так же, как и данные числа 5 и 9, является натуральным числом.
Выполняя пересечение множеств, мы по двум данным множествам находим новое, состоящее из общих элементов данных множеств.
Если рассмотреть вычитание натуральных чисел, то можно сказать, что при его выполнении по двум заданным натуральным числам находят третье - разность, но не всегда эта разность является натуральным числом. Но если рассмотреть вычитание целых чисел, то разность двух целых чисел всегда будет целым числом. И в этом вычитании целых чисел похоже на сложение натуральных чисел и пересечение двух множеств.
Обобщая, можно сказать, что, выполняя, ту или иную операцию, мы должны знать, на каком множестве она рассматривается. Далее, выполняя операцию, мы по двум элементам хну из выбранного множества находим третий элемент z того же множества. Он единственный, и при этом ответ, вообще говоря, зависит от порядка этих элементов (как, например, при вычитании чисел). Другими словами, при выполнении операции упорядоченной паре элементов из множества X ставится в соответствие единственный элемент того же множества. Операцию, удовлетворяющую таким условиям, называют алгебраической.
Определение. Алгебраической операций па множестве X называется соответствие, при котором каждой паре элементов из множества X сопоставляется единственный элемент того же множества.
Примерами алгебраических операций могут служить:
- сложение на множестве натуральных чисел, поскольку сумма любых натуральных чисел является натуральным числом. Иначе говоря, при сложении каждой паре (х, у) натуральных чисел ставится в соответствие единственное натуральное число, обозначаемое х + у;
- вычитание на множестве целых чисел, так как разность любых целых чисел является целым числом или, говоря иначе, при вычитании каждой паре (х, у) целых чисел ставится в соответствие единственное целое число, обозначаемое х-у;
- деление на множестве рациональных чисел при условии, что исключается деление на нуль. Тогда частное любых рациональных чисел есть рациональное число, т.е. каждой паре (х, у) рациональных чисел ставится в соответствие единственное рациональное число.
С понятием алгебраической операции связано понятие замкнутого множества: если на множестве X задана алгебраическая операция, то говорят, что множество X замкнуто относительно этой операции.
Например, о множестве N натуральных чисел можно сказать, что оно замкнуто относительно сложения и умножения.
Существуют операции, которые не являются алгебраическими. Примером такой операции является вычитание на множестве натуральных чисел хну будет натуральным числом лишь при условии, что х > у, т.е. в множестве натуральных чисел есть пары, которым нельзя поставить в соответствие натуральное число.
Вычитание на множестве натуральных чисел не является алгебраической операцией, но мы знаем, что если разность натуральных чисел существует, то это число единственное. Аналогичной особенностью обладает и деление натуральных чисел. Говорят, что вычитание и деление есть частичные алгебраические операции на множестве натуральных чисел.
Определение. Частичной алгебраической операцией на множестве X называется соответствие, при котором некоторым парам элементов из множества X сопоставляется единственный элемент того же множества.
Задача. На множестве X натуральных чисел, кратных 3, заданы операции: сложение, умножение, вычитание и деление. Какие из них являются на этом множестве:
а) алгебраическими;
б) частичными алгебраическими?
Решение. Любое натуральное число, кратное 3, имеет вид 3n, где n 
N.
Пусть 3n и 3m - два натуральных числа из множества X, n N, m N. Тогда 3n + 3m = 3(n + m), причем n + m - сумма двух натуральных чисел и, значит, число натуральное и единственное. Следовательно, складывая два любых натуральных числа, кратных 3, мы всегда получаем число, кратное 3, и это число единственное. Таким образом, сложение на данном множестве Х есть алгебраическая операция.
Рассмотрим произведение двух чисел из множества X: 3n∙3m=3(n+ m), причем n∙m - произведение двух натуральных чисел и, значит, число натуральное и единственное. Но 9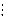 
3, следовательно, умножая два любых натуральных числа, кратных 3, мы всегда получаем число, кратное 3, и это число единственное. Таким образом, умножение на данном множестве X есть алгебраическая операция.
Рассмотрим теперь разность двух чисел из множества X: 3n-3m=3(n- m), но разность n-m существует на множестве натуральных чисел лишь при условии, что n > m. И если эта разность существует, то она единственна. Поэтому, если n> m, то разность 3n - 3m существует и является числом, кратным 3.
Таким образом, вычитание на множестве X есть частичная алгебраическая операция.
Выполним деление чисел на множестве X: 3n:3m = n:m. Так как частное натуральных чисел n и m существует не всегда и, кроме того, если оно существует, то оно может быть не кратно 3. Значит, деление на множестве чисел, кратных 3, не является алгебраической операцией. Но поскольку для некоторых n и m их частное может быть кратно 3 (например, если п = 24, m = 2), то деление на множестве X является частичной алгебраической операцией.
Понятие алгебраической операции проходит через весь школьный курс математики. Начинается этот процесс в начальных классах, где происходит знакомство детей со сложением, которое сначала рассматривается на отрезке натурального ряда от 1 до 9 включительно, затем на отрезке от 1 до 100 и т.д. Алгебраической эта операция становится тогда, когда ее начинают рассматривать на всем множестве натуральных чисел. С умножением ситуация аналогичная.
Операции вычитания и деления в начальном обучении рассматриваются как частичные алгебраические операции на множестве натуральных чисел.
