Пусть искомая величина f определяется из прямых измерений величины a,т.е. f = f(a). Разлагая f(a) в ряд Тэйлора, получим в окрестности точку 
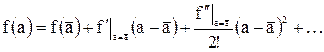(7)
Из (7) получим
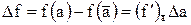(8)
Относительная погрешность величины f(a) равна
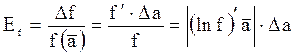(9)
Важно подчеркнуть, что доверительная вероятность для f такова же, что и для величины a.
Если искомая величина f = f(a, b,c…) - т.е. функция многих переменных (находится из результата прямых измерений величин a, b,c…), то найдя заданной доверительной вероятностью a = 0,95 полуширину доверительного интервала каждой из величин a, b,c... (погрешности Da, Db, Dc...), найдем величину погрешности Df и ef по формулам:
(10)
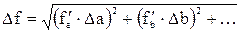(11)
Например,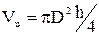 
. В данном случае проще сначала найти относительную погрешность 
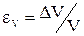согласно (11)
.
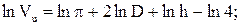
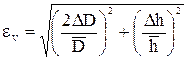Вычислив eV, найдем и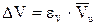 
. Погрешности Dh и DD найдем по (6).
При вычислении производных в (10), (11) все величины считаются постоянными, кроме той переменной, по которой находится производная.
Окончательный результат косвенных измерений величины запишем как и при прямых измерениях
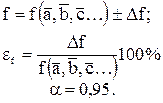
В заключении приведем порядок обработки результатов измерений.
Прямые измерения
1.Результаты каждого измерения записываются в таблицу. Цена наименьшего деления прибора как правило записывается в таблицу. Поэтому, во-первых, результаты измерения необходимо записывать до наименьшей цены деления прибора, во-вторых, не следует “на глаз” находить доли деления.
2.Находится среднее арифметическое из результатов проведенных измерений.
3.Находятся погрешности результатов отдельных измерений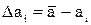 
и их квадраты 
.
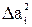4.Задается значение доверительной вероятности a = 0,95 и по заданной a и числу измерений n по таблице определяется коэффициент Стьюдента.
5.По формуле (6) находят полуширину доверительного интервала Da искомой величины (абсолютную погрешность результата), относительную погрешность e и записывают окончательный результат.
Косвенные измерения
1.Для каждой серии прямых измерений величин a,b,c..., входящих в расчетную формулу, искомой величины f, проводится обработка результатов так, как это описано выше. При этом для всех измеряемых величин задают одно и то же значение надежности a.
2.Находится выражение для абсолютной и относительной погрешности искомой величины согласно (10) и (11).
3.Вычисляются абсолютная и относительная погрешности результата косвенных измерений и записывается окончательный результат.
Примечание. Так как при n £ 10 значение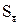 
определяется с погрешностью более 30%, то следует выполнять три правила:
- погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной - если первая есть 3 и более;
- результат измерения округляется до того же десятичного разряда, которым оканчиваются округленное значение абсолютной погрешности;
- округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним - двумя лишними знаками.
При сложении и вычитании приближенных чисел окончательный результат округляется так, чтобы он не имел значащих цифр в тех разрядах, которые отсутствуют хотя бы в одном из приближенных данных. При других математических операциях в результате оставить столько значащих цифр, сколько их осталось после операций сложения и вычитания в наименее точном числе.
