Номер периода 
| Уровень 
| Абсолютное изменение к предыдущему периоду | Цепные темпы, % к предыдущему | Уско- рение | Прирост ускорения к предыдущему периоду |
| 120,00 | +20,00 | - | - | ||
| 144,00 | +24,00 | +4,00 | - | ||
| 172,80 | +28,80 | +4,80 | +0,80 | ||
| 207,36 | +34,56 | +4,76 | +0,96 | ||
| 248,83 | +41,47 | +6,81 | + 1,15 | ||
| 298,60 | +49,77 | + 8,30 | + 1,39 |
Таблица 7.7.
Экспоненциальный тренд при k<1: 
| Номер периода | Уровень

| Абсолют- ные изме- нения (цепные) | Цепные темпы, % к предыдущему периоду | Уско- рение | Замедление ускорения |
| 160,00 | -40,00 | - | - | ||
| 128,00 | -32,00 | +8,00 | - | ||
| 102,40 | -25,60 | +6,40 | -1,60 | ||
| 81,92 | -20,48 | +5,12 | -1,28 | ||
| 65,54 | -16,38 | +4,10 | -1,02 | ||
| 52,43 | -13,11 | +3,27 | -0,83 |
По своему существу экспоненциальное развитие процесса и есть предельно возможное, предельно благоприятное по условиям развития, так как оно осуществляется в среде, не ограничивающей развитие данного процесса. Но следует помнить, что это происходит только до определенного времени, так как каждая среда, каждый ресурс в природе ограничен. Единственный спорный в науке процесс, по которому до сих пор нет доказательства ограниченности его во времени, - это экспоненциальное замедляющееся расширение Вселенной. Ограничено ли оно и сменится ли со временем сжатием или будет продолжаться бесконечно, зависит от значения средней плотности вещества и излучения во Вселенной, которую пока науке установить не удалось, ибо не все формы существования вещества и полей известны. Зато интересно знать, что самый фундаментальный процесс, охватывающий всю известную Вселенную, уже по крайней мере 12-15 млрд. лет развивается по экспоненте.
Для нахождения параметров «a» и «k» уравнение экспоненциального тренда логарифмируем:
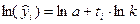 (7.18).
(7.18).
В такой форме, т.е. для логарифмов, уравнение соответствует линейному, следовательно, метод наименьших квадратов дает для логарифмов «а» и «k» нормальные уравнения, аналогичные для параметров aи bлинейного тренда:
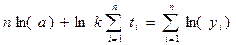 (7.19),
(7.19),
 (7.20).
(7.20).
Так как номера периодов времени не логарифмируются, можноперенести начало отсчета в середину ряда и упростить систему:
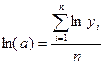 ;
; 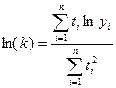 (7.21).
(7.21).
Приведем пример расчета экспоненциального тренда по данным рис. 7.4 (табл. 7.8).
Таблица 7.8.
Расчет экспоненциального тренда численности населения
Земли в 1950-2000 г.
| Год | 
| 
| 
| 
| 
| Тренд
 млн. чел.
млн. чел.
| Отклонение от тренда,
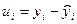
|

|
| - 2.5 | -6317,5 | 7,835 | -19,588 | -38 | ||||
| -1.5 | -4590,0 | 8,026 | -12,339 | -5 | ||||
| -0. 5 | -1863,5 | 8,223 | -4,112 | +64 | ||||
| 0.5 | 8.396 | 4.198 | +53 | |||||
| 1.5 | 7711.5 | 8.564 | 12.846 | +10 | ||||
| 2.5 | 8.726 | 21.815 | -90 | |||||

| 12555.5 | 49.77 | 3.12 | -6 |
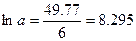 или а = 4004;
или а = 4004;
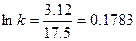 или k = 1.195.
или k = 1.195.
Уравнение тренда:  .
.
Итак, население Земли в период времени с 1950 по 2000 г. Возрастало со среднегодовым темпом роста, равным корню десятой степени из среднего темпа за десятилетие, найденного по данным таблицы 7.8, т.е. 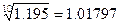 или 1.8% прироста в год. Прогнозировать дальнейшую динамику численности населения по рассчитанному тренду не стоит, так как уже в начале XXI века темп прироста стал замедляться. По прогнозам Венского Международного института прикладного системного анализа, наиболее вероятный вариант роста населения Земли в нашем веке – постепенное замедление до полного его прекращения к 2100 году при уровне населения 11.5 млрд. чел., а затем снижение числа жителей Земли до 5 млрд. чел.
или 1.8% прироста в год. Прогнозировать дальнейшую динамику численности населения по рассчитанному тренду не стоит, так как уже в начале XXI века темп прироста стал замедляться. По прогнозам Венского Международного института прикладного системного анализа, наиболее вероятный вариант роста населения Земли в нашем веке – постепенное замедление до полного его прекращения к 2100 году при уровне населения 11.5 млрд. чел., а затем снижение числа жителей Земли до 5 млрд. чел.
7.4. Гиперболический тренд и его свойства.
Из различных форм гипербол рассмотрим только наиболее простую:
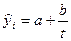 (7.22).
(7.22).
Если основной параметр гиперболы b>0, то этот тренд выражает тенденцию замедляющегося снижения уровней и при 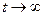 ,
, 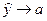 . Таким образом, свободный член гиперболы - это предел, к которому стремится уровень тренда.
. Таким образом, свободный член гиперболы - это предел, к которому стремится уровень тренда.
Такая тенденция наблюдается, например (рис. 7.5), при изучении процесса снижения затрат любого ресурса (труда, материалов, энергии) на единицу данного вида продукции или ее себестоимости в целом. Затраты ресурса не могут стремиться к нулю, значит, экспонента не соответствует сущности процесса; нужно применить гиперболическую формулу тренда.
Если параметр b<0, то с возрастанием t, т.е. с течением времени, уровни тренда возрастают и стремятся к величине «а» при 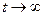 .
.
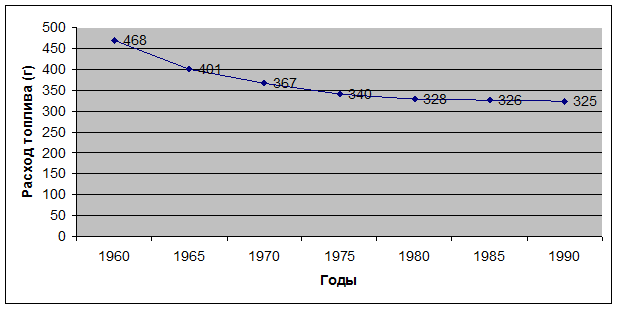
Рис. 7.5. Динамика расхода условного топлива на производство электроэнергии
(г на 1 кВт-ч) на электростанциях региона.
Такой характер динамики присущ, например, показателям КПД двигателей или иных преобразователей энергии (трансформатор тока, фотоэлемент и т.п.). По мере развития научно-технического прогресса эти КПД постепенно повышаются, не никогда не могут превысить определенного предела для каждого типа двигателя и не могут превысить 100% для любого преобразователя энергии. При расчете гиперболического тренда нельзя нумеровать года от середины ряда, так как значения - должны быть всегда положительными.
Основные свойства гиперболического тренда:
1. Абсолютный прирост или сокращение уровней, ускорение абсолютных изменений, темп изменения - все эти показатели не являются постоянными. При b>0 уровни замедленно уменьшаются, отрицательные абсолютные изменения, а также положительные ускорения тоже уменьшаются, цепные темпы изменения растут и стремятся к 100%.
2. При b<0 уровни замедленно возрастают, положительные абсолютные изменения, а также отрицательные ускорения и цепные темпы роста замедленно уменьшаются, стремясь к 100%.
Как видим, гиперболический тренд описывает в любом случае тенденцию такого процесса, показатели которого со временем затухают, т.е. происходит переход от движения к застою. Иллюстрацией этих свойств может служить табл. 7.9.
Таблица 7.9.
Показатели динамики при гиперболическом тренде.
Номер периода 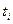
| Уровень 
| Абсолютное изменение к предыдущему периоду | Цепные темпы, % к предыдущему | Ускорение |
| 200,0 | - | - | - | |
| 2 | 150,0 | -50,0 | 75,0 | - |
| 133,0 | -16,7 | 88,9 | +33,3 | |
| 125,0 | -8,3 | 93,8 | +8,4 | |
| 120,0 | -5,0 | 96,0 | +3,3 | |
| 116,7 | -3,3 | 97,2 | + 1,7 |
Уравнение гиперболического тренда отличается от линейного уравнения тем, что вместо tв первой степени оно включает номера периодов времени (моментов) в минус первой степени. Соответственно нормальные уравнения метода наименьших квадратов примут вид:
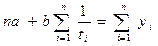 (7.23),
(7.23),
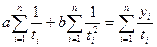 (7.24).
(7.24).
Однако при этом нельзя, в отличие от линейного тренда, переносить начало отсчета периодов времени в середину, так как гипербола не имеет постоянного параметра изменения уровней на протяжении всего периода, и все величины 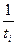 должны быть положительными.
должны быть положительными.
Рассмотрим расчет гиперболического уравнения тренда (табл. 7.10) по данным рис. 7.5 - динамика расхода условного топлива на производство электроэнергии на электростанциях региона (г на 1 кВт-ч).
Таблица 7.10.
Расчет гиперболического уравнения тренда.
| Год | 
| 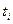
| 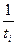
| 
| 
| Тренд,

| Отклонение от тренда,
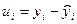
|

|
| 1,000 | 1,000 | -5 | ||||||
| 0,500 | 0,250 | +14 | ||||||
| 0,333 | 0,111 | +8 | ||||||
| 0,250 | 0,062 | -4 | ||||||
| 0,200 | 0,040 | -8 | ||||||
| 0,167 | 0,028 | _4 | ||||||
| 0,143 | 0,020 | -1 | ||||||

| - | 2,593 | 1,511 |
Нормальные уравнения МНК:
7а + 2,593 b = 2555,
2,593а + 1,511 b = 1041.
Решая систему уравнений, получаем: а = 301,3; b = 171,9. Уравнение гиперболического тренда удельного расхода топлива имеет вид:
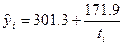
Величина удельного расхода 301,3 - это предел, к которому стремится экономия топлива при данной технологии тепловых электростанций региона. Существенного резерва экономии уже нет.
7.5. Логарифмический тренд и его свойства.
Если изучаемый процесс приводит к замедлению роста какого-то показателя, но при этом рост не прекращается, не стремится к какому-либо ограниченному пределу, то гиперболическая форма тренда уже не подходит. Тем более не подходит парабола с отрицательным ускорением, по которой замедляющийся рост перейдет со временем в снижение уровней. В указанном случае тенденция изменения лучше всего отображается логарифмической формой тренда:
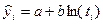 (7.25).
(7.25).
Логарифмы возрастают значительно медленнее, чем сами числа (номера периодов), но рост логарифмов неограничен. Подбирая начало отсчета периодов (моментов) времени, можно найти такую скорость снижения абсолютных изменений, которая наилучшим образом отвечает фактическому временному ряду.
Примером тенденций, соответствующих логарифмическому тренду, может служить динамика рекордных достижений в спорте: известно, что увеличение на 1 см рекорда прыжка в высоту пли снижение на 0,1 с времени бега на 200 или 400 м требует все больших и больших затрат времени, каждый рекорд дается все большим и большим трудом. В то же время нет и «вечных» рекордов, все спортивные достижения улучшаются, но медленнее и медленнее, т.е. по логарифмическому тренду. Нередко такой же характер динамики присущ на отдельных этапах развития сельского хозяйства, например, урожайности или валового сбора какой-то культуры в данном регионе, пока новое агротехническое достижение не придаст тенденции ускорение.
Основные свойства логарифмического тренда:
1. Если b>0, то уровни возрастают, но с замедлением, а если b<0, то уровни тренда уменьшаются, тоже с замедлением.
2. Абсолютные изменения уровней по модулю всегда уменьшаются со временем.
3. Ускорения абсолютных изменений имеют знак, противоположный самим абсолютным изменениям, а по модулю постепенно уменьшаются.
4. Темпы изменения (цепные) постепенно приближаются к
100% при 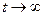 .
.
Можно сделать общий вывод о том, что логарифмический тренд отражает, так же как и гиперболический тренд, постепенно затухающий процесс изменений. Различие состоит в том, что затухание по гиперболе происходит быстро при приближении к конечному пределу, а при логарифмическом тренде затухающий процесс продолжается без ограничения гораздо медленнее.
Особенность этого типа тренда заключается в том, что логарифмировать необходимо номера периодов (моментов) времени. Следовательно, все номера должны быть положительными числами. Однако это вовсе не означает, что нумерацию следует начинать с числа 1. Дело в том, что величина логарифма быстро возрастает при переходе от единицы к двум: натуральный логарифм единицы равен нулю, а логарифм двух равен 0,693, имеем рост на 0,693; в то же время логарифм четырех равен 1,386, а логарифм пяти равен 1,609, имеем прирост лишь на 0,223 и т.д. Если уровень изучаемого ряда вначале возрастает втрое быстрее, чем между четвертым и пятым периодом, тогда нумерация от единицы допустима. Если же уменьшение роста уровней происходит значительно медленнее, нумерацию периодов (моментов) следует начинать не с единицы, а с большего числа.
Покажем методику расчета логарифмического уравнения тренда на примере динамики валового сбора чая в Китае (см. табл. 7.11).
Таблица 7.11.
Расчет логарифмического тренда валового сбора чая в Китае
| Год |  (в тыс. т.)
(в тыс. т.)
| 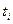
| 
| 
| Отклонение от тренда,
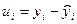
|

| 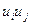
|
| 5 | 1 | ||||||
| 1,386 | |||||||
| 1,609 | -50 | ||||||
| 1,792 | -10 | ||||||
| 1,946 | -6 | -102 | |||||
| 2,079 | -102 | ||||||
| 2,197 | -6 | ||||||
| 2,303 | -17 | ||||||
| 2,398 | -21 | ||||||
| 2,485 | -12 | -216 | |||||
| 2,565 | |||||||
| 2,639 | |||||||
| 2,708 | |||||||
| 2,773 | -11 | ||||||
| 2,833 | -11 | ||||||
| 2,890 | -6 | -132 | |||||
| 2,944 | -44 | ||||||
| 2,996 | -2 | — | |||||
| Итого | - | - | k=6 | 652,6 |
Временной ряд, прежде всего, нужно разделить на несколько частей, например, на три части, и в каждой части вычислить средний уровень, тыс. т:
1978-1983 гг. - 331,7 т.;
1984-1989 гг. - 482,7 т.;
1990-1994 гг. - 566,0. т.
Эти усредненные уровни относятся соответственно к середине между 1980 и 1981 гг., к середине между 1986 и 1987 гг. и к 1992 г. Если первую дату обозначить годом номер х, то вторая будет годом номер х + 6, а третья - годом номер х + 11,5. Исходя из уравнения логарифмического тренда, имеем уравнения:
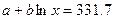 (7.26),
(7.26),
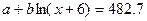 (7.27),
(7.27),
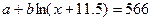 (7.28).
(7.28).
Вычитая из второго уравнения первое, получим:
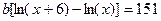 . (7.29).
. (7.29).
Вычитая второе уравнение из третьего, получим:
 (7.30).
(7.30).
Делим второй результат на первый:
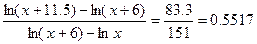 (7.31).
(7.31).
Теперь необходимо подобрать такое значение переменной «х», при котором выполняется вышеприведенное равенство. Искомое значение х = 6.5. Подставляя величину «х» в уравнения (7.29) вычислим значения параметра b: b = 230.9 и b = 228.4. Среднее из этих двух значений равно 229.6. Теперь, подставляя значения «х» и b в уравнения (7.26-7.28) получим три оценки параметра «а»: а = -98.1; -97.2; -97.6. Средняя величина а = -97.6.
Уравнение логарифмического тренда имеет вид:
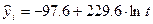 .
.
7.6. Логистический тренд и его свойства.
Логистическая форма тренда подходит для описания такого процесса, при котором изучаемый показатель проходит полный цикл развития, начиная, как правило, от нулевого уровня, сначала медленно, но с ускорением возрастая, затем ускорение становится нулевым в середине цикла, т.е. рост происходит по линейному тренду, затем, в завершающей части цикла, рост замедляется по гиперболе по мере приближения к предельному значению показателя.
Примером такого цикла динамики может служить изменение доли грамотного населения в стране, например в России, с 1800 г. до наших дней, или изменение доли семей, имеющих телевизоры, примерно с 1945 до 2000 г. в России и т.д. В некоторых зарубежных программах для компьютеров логистическая кривая называется S-образной кривой.
Можно, конечно, логистическую тенденцию считать объединением трех разных по типу тенденций: параболической с ускоряющимся ростом на первом этапе, линейной - на втором и гиперболической с замедляющимся ростом - на третьем этапе. Но есть доводы и в пользу рассмотрения всего цикла развития как особого единого типа тенденции со сложными переменными свойствами, но постоянным направлением изменений в сторону увеличения уровней в рассмотренных нами примерах. Рассмотрение таких временных рядов, как проявление единой логистической тенденции, позволяет уже на первом этапе рассчитать всю траекторию развития, определить сроки перехода от ускоренного роста к замедленному, что чрезвычайно важно при планировании производства или реализации нового вида товара, спрос на который будет проходить все этапы логистической тенденции вплоть до насыщения рынка. Так, например, обеспеченность населения в России автомобилями в конце 1980-х годов находилась на начальном этапе логистической кривой, и это означало, что предстоит еще ряд лет или даже десятилетий ускоренного роста спроса. В то же время обеспеченность фотоаппаратами уже достигла этапа замедления роста, и это означало, что расширять производство или импорт прежних типов фотоаппаратов не следует. Расширение их рынка возможно было только для принципиально новых типов фотоаппаратов, насыщенность которыми еще находится в самом начале первого этапа.
В вышеописанном диапазоне изменения уровней, т.е. от нуля до единицы, уравнение логистического тренда имеет вид:
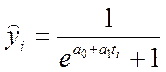 (7.32).
(7.32).
Если же диапазон изменения уровней ограничен не нулем и единицей, а любыми значениями, определяемыми исходя из существа задачи, обозначаемыми утах и утiп, то формула логистического тренда принимает вид:
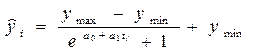 (7.33).
(7.33).
Таблица 7.12.
Показатели динамики при логистическом тренде: 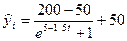 .
.
Номер периода 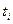
| Уровень 
| Абсолютное изменение к предыдущему периоду | Ускорение | Темп роста к предыдущему периоду, % |
| 51,0 | - | - | - | |
| 54,4 | +3,4 | - | 106,7 | |
| 67,9 | + 13,5 | + 10,1 | 124,8 | |
| 106,6 | +38,7 | +25,2 | 157,0 | |
| 159,7 | +53,1 | + 14,4 | 149,8 | |
| 188,6 | +28,8 | -24,2 | 118,1 | |
| 197,3 | +8,7 | -20,2 | 104,6 | |
| 199,4 | +2,1 | -6,6 | 101,1 |
Как видно из табл. 7.12, абсолютные изменения нарастают до середины периода, затем уменьшаются. Все они положительны. Ускорения сначала возрастают, а после середины периода снижаются, становятся отрицательными, но уменьшаются по модулю. Сумма положительных и отрицательных ускорений приближенно равна нулю (если ряд продлить от  до +
до + 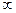 , то сумма их точно равна нулю). Темпы роста возрастают до конца первой половины ряда, затем снижаются. Если ряд достаточно длинный, то темпы начинаются со 100 % и завершаются на 100%.
, то сумма их точно равна нулю). Темпы роста возрастают до конца первой половины ряда, затем снижаются. Если ряд достаточно длинный, то темпы начинаются со 100 % и завершаются на 100%.
При логистическом тренде со снижающимися уровнями показатели динамики изменяются в следующем порядке: отрицательные абсолютные изменения по модулю возрастают до середины ряда и снижаются к концу, стремясь к нулю при 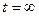 . Ускорения в первой половине периода отрицательные и по модулю возрастающие; во второй половине периода ускорении положительные и уменьшающиеся в пределе до нуля. Темпы изменений все меньше 100%, в конце первой половины периода наименьшие, во второй половине возрастающие с замедлением до 100% в пределе. Графическое изображение логистического тренда приведено на рис. 7.6.
. Ускорения в первой половине периода отрицательные и по модулю возрастающие; во второй половине периода ускорении положительные и уменьшающиеся в пределе до нуля. Темпы изменений все меньше 100%, в конце первой половины периода наименьшие, во второй половине возрастающие с замедлением до 100% в пределе. Графическое изображение логистического тренда приведено на рис. 7.6.

Рис. 7.6. Логистическая тенденция динамики доли тепловозной и электровозной тяги в грузообороте железных дорог СССР.
При расчете параметров логистического тренда логарифмируют величину, производную от уровней ряда, но не номера периодов (моментов), эту нумерацию поэтому рациональнее проводить от середины ряда. Особенностью логистического тренда является этап обоснования значений максимального и минимального уровней временного ряда. Это обоснование осуществляется на основе, во-первых, уровней фактического ряда, во-вторых, теоретических, т.е. внешних по отношению к статистике, соображении, относящихся к содержанию изучаемого процесса.
Уравнение логистического тренда в общем виде непосредственно логарифмировать невозможно. Преобразуем его в форму
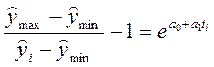 (7.34)
(7.34)
и обозначим его левую часть греческой буквой кси, т.е.
 или
или 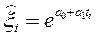 , а
, а 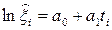
Условие метода наименьших квадратов:
 (7.35).
(7.35).
После вычисления частных производных по а0 и по а  , получаем нормальные уравнения МНК для логистической кривой, аналогичные для прямой линии, так как после проведения подстановки с использованием буквы кси, фактически проведена линеаризация функции логистической кривой:
, получаем нормальные уравнения МНК для логистической кривой, аналогичные для прямой линии, так как после проведения подстановки с использованием буквы кси, фактически проведена линеаризация функции логистической кривой:
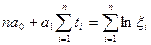 (7.36),
(7.36),
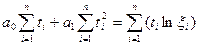 (7.37).
(7.37).
При переносе начала отсчета периодов (моментов) времени в середину ряда система упрощается до двух уравнений с одним неизвестным в каждом из них: 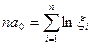 и
и 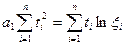 . Откуда:
. Откуда:
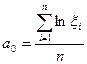 и
и 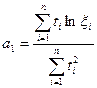 (7.38).
(7.38).
Алгоритм расчета логистической кривой состоит из десяти этапов:
1) выбор величин 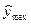 и
и  ;
;
2) вычисление по фактическому временному ряду значений
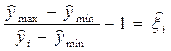
3) вычисление  ;
;
4) нумерация периодов или моментов времени от середины
ряда;
5) умножение  и
и 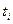 ;
;
6) подсчет итоговых сумм;
7) вычисление 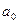 и
и 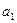 ;
;
8) вычисление 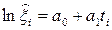 ;
;
9) вычисление 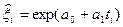 для всех периодов;
для всех периодов;
10)вычисление уровнем тренда по формуле (7.38).
Для практического закрепления материала рассчитать самостоятельно параметры логистического тренда, в соответствии с которым развивается динамика рыночных цен акций компании «АВС», приведенных во второй колонке таблицы 7.13.
Таблица 7.13.
Расчет логистического тренда.
| № месяца | 
| 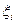
| 
| 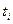
| 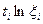
| 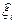
| 
| 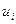
| 
|
| 15.0 | 17,00 | 2,833 | -6,5 | -18,416 | 16,803 | 15,1 | -0,10 | 0,01 | |
| 17,0 | 11,86 | 2,473 | -5,5 | -13,601 | 10,854 | 17,6 | -0,60 | 0,36 | |
| 20,0 | 8,00 | 2,079 | -4,5 | -9,357 | 7,017 | 21,2 | -1,20 | 1,44 | |
| 26,4 | 4,49 | 1,501 | -3,5 | -5,255 | 4,535 | 26,3 | +0,10 | 0,01 | |
| 33,5 | 2,83 | 1,040 | -2,5 | -2,601 | 2,931 | 32,9 | +0,60 | 0,36 | |
| 43,2 | 1,71 | 0,537 | -1,5 | -0,805 | 1,814 | 41,1 | +2,16 • | 4,41 | |
| 51,8 | 1,15 | 0,142 | -0,5 | -0,071 | 1,224 | 50,5 | + 1,30 • | 1,69 | |
| 61,8 | 0,74 | -0,305 | 0,5 | -0,152 | 0,791 | 60,3 | + 1,50 • | 2,25 | |
| 70,7 | 0,48 | -0,728 | 1,5 | -1,093 | 0,510 | 69,6 | + 1,10 • | 1,21 | |
| 78,9 | 0,31 | -1,183 | 2,5 | -2,958 | 0,330 | 77,7 | + 1,20 • | 1,44 | |
| 84,5 | 0,21 | -1,570 | 3,5 | -5,495 | 0,213 | 84,2 | +0,30 | 0,09 | |
| 88,8 | 0,14 | -1,951 | 4,5 | -8,779 | 0,138 | 89,1 | -0,30 | 0,09 | |
| 92,4 | 0,09 | -2,383 | 5,5 | -13,109 | 0,089 | 92,6 | -0,20 | 0,04 | |
| 94,4 | 0,07 | -2,713 | 6,5 | -17,633 | 0,058 | 95,1 | -0,70 | 0,49 | |

| 778,4 | - | -0,228 | 0,0 | -99,325 | - | 773,3 | - | 13,89 |
Уравнение логистического тренда динамики рыночной цены акции компании «АВС» имеет вид:
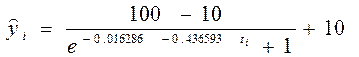 (7.39).
(7.39).
Напомним, что, в отличие от прямой и параболы, алгоритм расчета других кривых не предусматривает автоматического равенства сумм выравненных и фактических уровней, они совпадают только при идеальном выражении тенденции ряда данным уравнением тренда.
7.7. Методы распознавания типа колебаний.
Мы уже знаем, что временной ряд, как правило, содержит два основных элемента: тенденцию динамики и колеблемость. Эти составляющие в разных реальных временных рядах находятся в неодинаковом соотношении, а в крайних случаях остается один элемент: ряд без колеблемости уровней представляет собой тренд в чистом виде, а ряд без тенденции динамики, но с колебаниями уровней около постоянной средней величины - это стационарный временной ряд. Оба крайних случая крайне редки на практике. Обычно тенденция и колеблемость сочетаются в исходном ряду, и методы статистического анализа, изложенные в начале этой главы, призваны «очистить» тенденцию от колебаний, измерить ее параметры. Колеблемость в этом случае выступала как помеха, «шум», мешающий выделить и интерпретировать «сигнал», т.е. параметры тренда. Нередко в учебной литературе взгляд на колеблемость, как на помеху в изучении тенденции, преобладает или является единственным.
Однако сама колеблемость также представляет собой важный предмет статистического исследования временных рядов. Значение колеблемости многогранно:
1)  она позволяет выдвинуть гипотезы о причинах колебаний, о путях влияния на них;
она позволяет выдвинуть гипотезы о причинах колебаний, о путях влияния на них;
2) на основе параметров колеблемости ее можно прогнозировать или учитывать как фактор ошибки прогноза, т.е. сделать прогноз наиболее надежным и (или) точным;
3) на основе параметров и прогнозов колебаний можно рассчитать резервы, страховой запас, необходимый для преодоления вредных последствий колебания уровней, например объемов продаж.
Колебания уровней временного ряда могут иметь разную форму, разное распределение по времени, разную частоту и амплитуду. В данной главе рассматриваются методы исследования этих свойств колеблемости, их отображения в системе показателей, характеризующих колеблемость тех или иных явлений. Что же касается дальнейшего изучения причин, механизма колебаний, то эта задача выходит за пределы статистического исследования и должна выполняться наукой, изучающей те явления и процессы, динамика которых отражена временным рядом.
Графическое отображение и основные свойства
разных типов колебаний.
Так же, как изучение тенденции, исследование колебаний целесообразно начать с графического изображения - обобщающего, целостного впечатления о временном ряде. Все многообразие встречающихся колебаний во временных рядах можно представить как «смесь» в разных пропорциях трех основных типов:
• пилообразной или маятниковой колеблемости;
• долгопериодических циклов колебаний;
• случайно распределенной во времени колеблемости.
Графическое изображение каждого из этих типов и описание основных свойств каждого типа колеблемости, во-первых, помогают по виду фактического ряда определить, каков преобладающий в нем тип колебаний, во-вторых, помогают экономисту, менеджеру, другому специалисту понять, какие последствия могут иметь колебания для его сферы деятельности и как с этими колебаниями (если нужно) бороться.
7.7.1. Пилообразная колеблемость.
Характерной чертой этого типа колеблемости является правильное, регулярное чередование отклонений от тренда вверх и вниз, т.е. положительных по знаку и отрицательных, через одно. Поскольку это похоже на колебание маятника часов вправо-влево, данный тип колеблемости называют также маятниковой колеблемостью. Название же пилообразная происходит от вида графика (рис. 7.7), похожего на зубья пилы (хотя величина зубьев, разумеется, не должна быть, как у хорошей пилы, одинаковой).
Свойства пилообразной колеблемости таковы: из-за частой смены знака отклонения от тренда не происходит аккумуляции ни положительных, ни отрицательных отклонений. Следовательно, нет необходимости создавать для их компенсации значительный страховой запас. Регулярность чередования отклонений обеспечивает их надежное прогнозирование: если в данный период отклонение отрицательное, то в периоде 5 вперед оно будет положительным (данный период считать нулевым номером). Число положительных отклонений при достаточно большой длине ряда равно (точнее, стремится к равенству) числу отрицательных отклонений, а общее количество локальных экстремумов (отклонений от тренда, которые либо меньше, либо больше двух соседних по алгебраической величине) равно числу уровней.
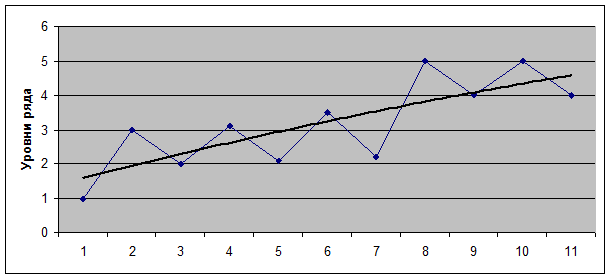
Рис. 7.7. Пилообразная колеблемость.
Причины пилообразной колеблемости зависят как от внутренних факторов системы, так и от внешних. Внутренние для биржевой системы причины пилообразной колеблемости цен акций - это поступление информации об основных параметрах производства и сбыта продукции данной корпорацией. Внешние причины пилообразной колеблемости цен акций на бирже – это изменение макроэкономических данных в стране, воздействие политических рисков, влияние конъюнктурных колебаний мирового финансового рынка.
Распознать наличие пилообразных колебаний как элемента во временном ряду можно, во-первых, по виду графика, во-вторых, подсчетом числа локальных экстремумов в ряду отклонений от тренда: чем это число ближе к числу уровней ряда, тем большую роль играют пилообразные колебания в их общем комплексе. Третий способ распознавания - по знаку и величине коэффициента автокорреляции отклонений от тренда первого порядка, т.е. со сдвигом (лагом) на 1 временной период.
Коэффициент автокорреляции отклонений рассчитывается по формуле:
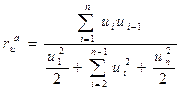 (7.40).
(7.40).
Числитель коэффициента - сумма произведений каждого отклонения на следующее, кроме последнего, в ряду отклонений. В этих произведениях первое отклонение и последнее, т.е. 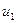 и
и 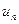 , участвуют только по одному разу, а все остальные отклонения - по два раза. Соответственно в знаменателе в сумму квадратов отклонений от 2 до n-1 входят квадраты с единичным весом, а квадраты первого и последнего отклонений – с половинным весом.
, участвуют только по одному разу, а все остальные отклонения - по два раза. Соответственно в знаменателе в сумму квадратов отклонений от 2 до n-1 входят квадраты с единичным весом, а квадраты первого и последнего отклонений – с половинным весом.
Чем ближе коэффициент автокорреляции к -1, тем большую роль играет пилообразная составляющая в общей колеблемости изучаемого временного ряда. При коэффициенте, по алгебраической величине превышающем 0.3, можно считать пилообразную составляющую несущественной или отсутствующей вовсе, если длина ряда не больше 20 уровней.
7.7.2. Долгопериодическая циклическая колеблемость.
Характерной чертой этого типа колебаний является наличие нескольких (многих) подряд отклонений одного знака, затем сменяющихся примерно таким же количеством отклонений противоположного знака подряд. Затем весь цикл вновь повторяется, причем, как правило, длина всех циклов одинакова или хотя бы примерно равная. Если равенство отдельных циклов существенно нарушается, говорят о квазициклической колеблемости, т.е. как бы циклической.
Свойства циклической колеблемости (рис. 7.8) таковы: отклонения одного и того же знака следуют подряд в течение примерно половины длины цикла. Следовательно, эти отклонения аккумулируются, и для их компенсации (если таковая требуется) нужен большой страховой запас. Например, надой молока от коров находится ниже тренда в течение 6 месяцев года (с октября до марта включительно) в большинстве сельхозпредприятий Ростовской области и других регионов России. Следовательно, для удовлетворения спроса на молоко в осенне-зимний период нужен запас в форме сухого молока, масла и других хранящихся молочных продуктов.
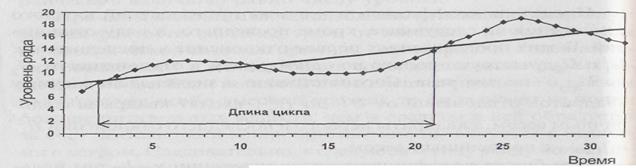
Рис. 7.8. Циклическая долгопериодическая колеблемость:
—•— фактические уровни
______ тренд.
Для прогнозирования циклическая колеблемость благоприятна, особенно если длина цикла строго постоянна. Прогноз на любой будущий период состоит из прогноза тренда и циклического отклонения от него, соответствующего фазе цикла в прогнозируемый период. Например, зная, что солнечная активность имеет 10-11-летнюю периодичность и что предыдущий цикл имел максимум в 2000-2001 гг., можно уверенно прогнозировать следующий максимум на 2010-2011 гг.
Как правило, за цикл наблюдаются два экстремума отклонений от тренда - один максимум и один минимум. Следовательно, за период, состоящий из N уровней, насчитывается экстремумов:
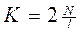 (7.41),
(7.41),
где l - длина цикла. Причиной циклической колеблемости является какая-либо основная сила, влияющая на уровень изучаемого явления. Иначе говоря, есть главный фактор, вызывающий колебания. Сезонные колебания температуры, осадков, а следовательно, и производства, и потребления многих видов продукции зависят от одного фактора - наклона земной оси к плоскости орбиты Земли. Причина циклической колеблемости солнечной активности пока науке не известна.
Распознать циклическую долгопериодическую колеблемость можно по виду графика, подсчетом числа экстремумов в ряду отклонений от тренда и по коэффициенту автокорреляции отклонений первого порядка. Если число локальных экстремумов в ряду отклонений мало, то можно предположить наличие циклической колеблемости. Поскольку отклонения одного и того же знака следуют подряд, их произведения являются положительными числами, а отрицательные произведения встречаются лишь дважды за цикл - при пересечении графиком фактического ряда уровней тренда вниз и вверх. Следовательно, коэффициент автокорреляции при долгопериодической колеблемости – величина положительная, стремящаяся к +1 при 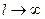 . При наличии фактического коэффициента больше чем +0,3 можно считать, что в общей колеблемости временного ряда есть существенная циклическая составляющая, а при
. При наличии фактического коэффициента больше чем +0,3 можно считать, что в общей колеблемости временного ряда есть существенная циклическая составляющая, а при 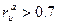 циклическая составляющая является главной.
циклическая составляющая является главной.
Для нахождения длины цикла, особенно если цикличность не строгая, а «квази», нужно последовательно вычислить коэффициенты автокорреляции отклонений от тренда разных порядков, т.е. с лагом 1, 2, 3 и т.д. периодов времени. Наибольший по абсолютной величине коэффициент автокорреляции выявит длину цикла.
7.1.3. Случайно распределенная во времени колеблемость.
Характерной чертой данного типа колебаний является хаотичность последовательности отклонений: после отрицательного отклонения от тренда может следовать снова отрицательное или даже два-три отрицательных отклонений, а может и положительное (два-три). Это как бы мелкие «куски» пилообразной и циклической колеблемости разных длин цикла, перемешанные друг с другом. Иногда случайно распределенную колеблемость и называют «интерференция колебаний» (термин, заимствованный из физики).
Для колеблемости, изображенной на рис. 7.9, характерны два свойства:
• из-за хаотического чередования знаков отклонений от тренда их взаимопогашение наступает только на достаточно длительном периоде, а на коротких отрезках отклонения могут аккумулироваться, например, могут быть три неурожайных года подряд или два-три высокоурожайных. Значит, необходимы довольно значительные резервы, страховые запасы для
гарантии от колебаний;
• случайно распределенная во времени, колеблемость неблагоприятна для прогнозирования, ибо в любом прогнозируемом периоде может осуществиться с равной вероятностью как положительное, так и отрицательное отклонение от тренда. В данном случае прогнозировать можно лишь интервал, в котором с заданной вероятностью может оказаться уровень.
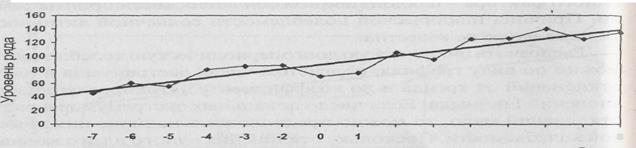
Рис. 7.9. Случайно распределенная во времени колеблемость.
Причиной случайно распределенных колебаний служит наличие большого комплекса независимых или слабосвязаниых между собой факторов, влияющих на уровни изучаемого явления. Так, колебания объемов продаж ценных бумаг на бирже зависят от фазы экономического цикла в стране, уровня инфляции, валютного курса, объема денежной массы, притока/оттока иностранного капитала, от времени года и еще от многих других факторов. Практика статистических исследований колеблемости объемов продаж ценных бумаг показала, что преобладают именно случайно распределенные колебания. Наличие множества примерно равноправных и независимых факторов означает также, что нельзя существенно уменьшить колеблемость, воздействуя только на какой-либо отдельный фактор. Необходимо, если это возможно, регулировать все основные факторы.
Распознать случайно распределенную во времени колеблемость по виду графика труднее, чем два других типа колебаний. Число локальных экстремумов может также колебаться. В среднем, как доказал английский статистик М. Кендэл, их число составляет  при среднем квадратическом отклонении, равном
при среднем квадратическом отклонении, равном  . Ряд, изображенный на рис. 7.9, имеет 10 локальных экстремумов (точек перегиба ломаной линии) при 2/3(15-2)=8,7 и среднем квадратичном отклонении, равном,
. Ряд, изображенный на рис. 7.9, имеет 10 локальных экстремумов (точек перегиба ломаной линии) при 2/3(15-2)=8,7 и среднем квадратичном отклонении, равном,  . Как видим, фактическое число экстремумов попадает в интервал х±
. Как видим, фактическое число экстремумов попадает в интервал х±  , т.е. вероятность того, что распределение отклонений от тренда является случайным, довольно велика, следовательно, эта гипотеза не может быть отклонена.
, т.е. вероятность того, что распределение отклонений от тренда является случайным, довольно велика, следовательно, эта гипотеза не может быть отклонена.
Коэффициент автокорреляции отклонений от тренда при случайно распределенной колеблемости стремится к нулю при  . Если ряд состоит менее чем из 19-22 уровней, коэффициенты автокорреляции первого порядка, не превышающие 0.3 по абсолютной величине, свидетельствуют о преобладании случайной компоненты в общем комплексе колебаний. В случае, изображенном на рис. 7.9,
. Если ряд состоит менее чем из 19-22 уровней, коэффициенты автокорреляции первого порядка, не превышающие 0.3 по абсолютной величине, свидетельствуют о преобладании случайной компоненты в общем комплексе колебаний. В случае, изображенном на рис. 7.9,  .
.
7.8. Измерение показателей силы и интенсивности колебаний.
Показатели силы и интенсивности колебаний аналогичны по построению, по форме показателям силы и интенсивности вариации признака в пространственной совокупности. По существу они отличаются тем, что показатели вариации вычисляются на основе отклонений от постоянной средней величины, а показатели, характеризующие колеблемость уровней временного ряда, - по отклонениям отдельных уровней от тренда, который можно считать «подвижной средней величиной».
Первый показатель - амплитуда (размах) колебаний - разность между наибольшим и наименьшим по абсолютной величине отклонениями от тренда. Например, размах колебаний объема экспорта из Японии за 1988-1995 гг. (см. табл. 7.6) составил: 5 - (-4) = 9 млрд дол. Размах колебаний затрат условного топлива на 1 кВт-ч электроэнергии (см. табл. 7.10) составил: 14 - (-8) = 22 гтоплива на 1 кВт-ч.
Показатель амплитуды колебаний характеризует лишь крайние пределы, но не среднюю силу колеблемости. Чем длиннее ряд, тем больше вероятность того, что в нем встретится особенно большое отклонение от тренда. Поэтому с увеличением длины изучаемого периода возрастает в среднем и амплитуда колебаний в отличие от всех других показателей колеблемости, которые не зависят от длины ряда.
Вторым показателем колеблемости по абсолютной величине (силе) является среднее по модулю отклонение от тренда, которое мы обозначим как а(t):
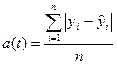 (7.42).
(7.42).
Знак tотличает указанный и все последующие показатели от аналогичного среднего по модулю отклонения от постоянной средней величины, меры силы вариации в пространственной совокупности. Средний модуль отклонений измеряется в тех же единицах, что уровни ряда. Например, согласно данным табл. 7.8 среднее по модулю отклонение от тренда численности населения Земли в 1950-2000 гг. может составить примерно 43.3 млн. чел.
Хотя средний модуль отклонений тренда вполне пригоден как обобщающий показатель силы колебаний за изучаемый период, но, как известно, модули имеют и существенные недостатки, в частности, с ними невозможно связать вероятностные законы распределения. Поэтому модули не пригодны для прогнозирования доверительных границ возможных колебаний с заданной вероятностью.
Чаще всего в качестве третьего показателя силы колебаний используется среднее квадратическое отклонение уровней ряда от тренда, обозначаемое как 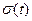 или
или  .
.
Если речь идет только об измерении колеблемости во временном ряду и не ставится задача оценки силы колебаний вообще в прогнозе на будущее, тогда следует вычислять и использовать обычное среднее квадратическое отклонение:
 (7.43).
(7.43).
Если же речь идет о вычислении оценки генерального показателя колеблемости, а исходный временной ряд рассматривается как выборка из генерального ряда, продолжаемого и в прошлое и в будущее, то следует учитывать потерю степеней свободы колеблемости и применять показатель:
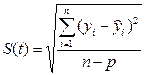 (7.44),
(7.44),
где р - число параметров в уравнении тренда.
Причину учета числа параметров тренда можно проиллюстрировать следующими примерами.
Линейный тренд имеет два параметра - а и b. Если из ряда уровней взять только уровни двух любых периодов, то, как известно из геометрии, прямая точно пройдет через две любые точки, мы увидим только тренд и не увидим никаких колебаний. Аналогично, если оставить от ряда три любых уровня, тренд в форме параболы II порядка, имеющий три параметра, точно пройдет через три точки графика, в результате колеблемость останется «за кадром», так как у нее нет ни одной степени свободы. Поэтому, оценивая генеральное среднее квадратическое отклонение уровней от тренда, нужно учесть потерю степеней свободы колебаний на величину, равную количеству параметров уравнения тренда. Именно такая несмещенная оценка генерального параметра может быть распространена на будущие периоды, т.е. она необходима в прогнозировании. Среднее квадратическое отклонение, как известно, входит в формулу нормального закона распределения вероятностей, на его основе можно рассчитывать вероятности ошибок прогнозов и их доверительные границы.
Показатели относительной интенсивности колебаний.
Показатели относительной интенсивности вариации рассчитываются как отношение ее абсолютных показателей к постоянной средней величине, относительной интенсивности колебаний - как отношение индивидуальных отклонений отдельного периода к уровню тренда за этот же период, а обобщающие показатели - как отношение обобщающих показателей силы колебаний за весь ряд к обобщающему показателю уровней ряда - среднему уровню.
Напомним, что при криволинейном тренде средний уровень не равен свободному члену уравнения тренда, так же как и при прямолинейном тренде, но при отсчете периодов от начала, а не от середины ряда. В этих случаях делить обобщающий показатель силы колебаний S(t)нужно не на свободный член уравнения, а на средний уровень изучаемого показателя. Аналогично коэффициенту пространственной вариации отношение среднего квадратического отклонения от тренда к среднему уровню временного ряда называют коэффициентом колеблемости, который обозначается для отличия от коэффициента пространственной вариации, как V(t). Его формула для оценки генеральной величины:
 (7.45).
(7.45).
В заключение необходимо подчеркнуть, что любая погрешность в определении типа тренда или при расчете его параметров приводит к преувеличению показателей силы и интенсивности колебаний. Так как реальные временные ряды всегда отклоняются от строго линейной, параболической, экспоненциальной или иной любой линии, то колеблемость всегда несколько преувеличивается за счет неполного соответствия истинной тенденции динамики какому-либо принятому типу линии тренда. Например, наверняка часть колеблемости численности населения Земли на самом деле объясняется тем, что «истинная» тенденция роста населения не являлась за 1950-2000 гг. строго экспоненциальной.
7.9. Представление синусоидальных колебаний в форме тригонометрического уравнения Фурье.
Выдающийся французский математик Жан Батист Жозеф Фурье (1768-1830) предложил метод преобразования периодических функций в ряд тригонометрических уравнений, называемых гармониками. Этот метод подходит для аналитического выражения сезонных колебаний, имеющих синусоидальную форму. Исходным рядом для преобразования Фурье лучше всего принять не первичный ряд за несколько лет, а усредненный ряд месячных уровней, в котором исключен тренд и (или) в основном погашены случайные колебания. Рассмотрим сезонные колебания рыночной цены некоторой акции (табл. 7.14).
Таблица 7.14.
Преобразование сезонных колебаний в ряд Фурье
| Месяц | Рыночная цена акции | 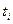 , градусов , градусов
|
cos 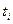
|
sin 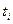
|
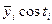
|
|

|

| ||||
| Январь | 1,000 | 0,000 | ||||||||||
| Февраль | 0,866 | 0,500 | -4 | |||||||||
| Март | 0,500 | 0,866 | 157,5 | |||||||||
| Апрель | 0,000 | 1,000 | -5 | |||||||||
| Май | -0,500 | 0,866 | -196 | |||||||||
| Июнь | -0,866 | 0,500 | -349 | 201,5 | -1 | |||||||
| Июль | -1,000 | 0,000 | -398 | |||||||||
| Август |
|
|
|
|
|
Дата добавления: 2017-03-12; Мы поможем в написании ваших работ!; просмотров: 1003 | Нарушение авторских прав
Лучшие изречения:
Ген: 0.015 с.






