КОНСПЕКТ ЗА 04.02.2017
Квадратні нерівності
Нехай потрібно розв’язати нерівність  (аналогічні міркування проводяться при розв’язуванні нерівностей
(аналогічні міркування проводяться при розв’язуванні нерівностей 

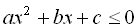 ). У залежності від знака дискримінанта квадратного тричлена
). У залежності від знака дискримінанта квадратного тричлена  потрібно розглянути два випадки:
потрібно розглянути два випадки:
1) Якщо  , а старший коефіцієнт а додатний, то при всіх значеннях х виконується нерівність
, а старший коефіцієнт а додатний, то при всіх значеннях х виконується нерівність  .
.
2) Якщо 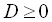 , то для розв’язання нерівності
, то для розв’язання нерівності  потрібно розкласти квадратний тричлен
потрібно розкласти квадратний тричлен  на множники за формулою
на множники за формулою  , потім поділити обидві частини нерівності
, потім поділити обидві частини нерівності  на число а, зберігши знак нерівності, якщо
на число а, зберігши знак нерівності, якщо  , і змінивши знак нерівності на додатний, якщо
, і змінивши знак нерівності на додатний, якщо  , і перейти до нерівності
, і перейти до нерівності  .
.
Приклад 7. Розв’язати нерівність  .
.
Розв’язання
Розв’язавши квадратне рівняння  , одержимо корені
, одержимо корені  . Тоді квадратний тричлен розкладеться на такі множники:
. Тоді квадратний тричлен розкладеться на такі множники:  .
.
Звідси, 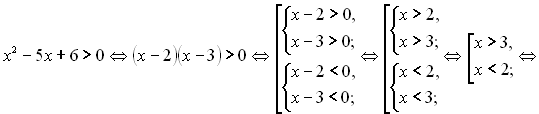


Відповідь: 
Квадратні нерівності, а також нерівності вищих степенів можна розв’язувати методом інтервалів (методом проміжків). В його основі лежить така властивість двочлена 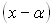 : точка
: точка  ділить числову вісь на дві частини – праворуч від точки? двочлен
ділить числову вісь на дві частини – праворуч від точки? двочлен  , а ліворуч від точки?
, а ліворуч від точки?  .
.

Приклад 8. Розв’язати нерівність  .
.
Розв’язання
Многочлен  перетворюється в нуль у точках
перетворюється в нуль у точках 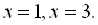 Ці точки розбивають координатну пряму на проміжки (
Ці точки розбивають координатну пряму на проміжки ( 1),
1),
(1; 3), (3;  ), усередині кожного з яких функція
), усередині кожного з яких функція  зберігає знак.
зберігає знак.

Оскільки в проміжку (3;  ) співмножники
) співмножники 
 додатні, то їхній добуток додатний, тобто
додатні, то їхній добуток додатний, тобто 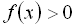 . Відзначимо проміжок (3;
. Відзначимо проміжок (3;  ) знаком “+”. Далі знаки в проміжках чергуються. Проводимо через визначені точки “криву знаків”. На тих проміжках, де ставиться знак “+”, виконується нерівність
) знаком “+”. Далі знаки в проміжках чергуються. Проводимо через визначені точки “криву знаків”. На тих проміжках, де ставиться знак “+”, виконується нерівність 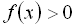 ; на тих проміжках, де знак “– “, виконується нерівність
; на тих проміжках, де знак “– “, виконується нерівність  . Отже, розв’язком початкової нерівності є об’єднанням проміжків: (
. Отже, розв’язком початкової нерівності є об’єднанням проміжків: ( 1), (3;
1), (3;  ).
).
Відповідь:  (
( 1)
1)  (3;
(3;  ).
).
Приклад 9. Розв’язати нерівність  .
.
Розв’язання
Якщо прирівняти до нуля многочлен  , то дискримінант виявиться від’ємним. А це означає, що квадратний тричлен додатний при всіх дійсних значеннях змінної х, тому при
, то дискримінант виявиться від’ємним. А це означає, що квадратний тричлен додатний при всіх дійсних значеннях змінної х, тому при  нерівність розв’язків не має.
нерівність розв’язків не має.
Відповідь: нерівність розв’язків не має.
Приклад 10. Розв’язати нерівність 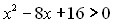 .
.
Розв’язання
Многочлен 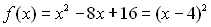 є невід’ємним при будь-якому дійсному значенні змінної х, томунерівність
є невід’ємним при будь-якому дійсному значенні змінної х, томунерівність  справджується при всіх дійсних значеннях змінної х, крім 4.
справджується при всіх дійсних значеннях змінної х, крім 4.
Відповідь: 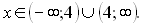
Приклад 11. Розв’язати нерівність  .
.
Розв’язання
Многочлен  перетворюється в нуль в точках
перетворюється в нуль в точках 

 . Ці точки розбивають координатну пряму на чотири проміжки. Оскільки даний многочлен містить множник у парному степені– це
. Ці точки розбивають координатну пряму на чотири проміжки. Оскільки даний многочлен містить множник у парному степені– це  , то при переході «змійки» через “0” знак не буде змінюватись. Зазначимо, що точка
, то при переході «змійки» через “0” знак не буде змінюватись. Зазначимо, що точка  входить у множину розв’язків, тому що при
входить у множину розв’язків, тому що при  дістаємо
дістаємо  .
.

Відповідь: 


 .
.
Приклад 12. Розв’язати нерівність 
Розв’язання
Наносимо точки  6; 2; 0; –1; –5 на числову вісь. Відзначимо точки
6; 2; 0; –1; –5 на числову вісь. Відзначимо точки  і
і  , при переході через них «змійки» знаки не будуть змінюватись. За допомогою «кривої знаків» дістаємо розв’язки, які позначені на рисунку зі знаком «+».
, при переході через них «змійки» знаки не будуть змінюватись. За допомогою «кривої знаків» дістаємо розв’язки, які позначені на рисунку зі знаком «+».

Відповідь: 
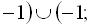

 .
.
Метод заміни змінної при розв’язанні раціональних нерівностей
Приклад 13. Розв’язати нерівність 
Розв’язання
Зробимо заміну 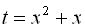 , тоді
, тоді  . Розкладемо на множники квадратний тричлен, який стоїть у лівій частині нерівності:
. Розкладемо на множники квадратний тричлен, який стоїть у лівій частині нерівності:  або
або 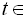


 .
.
Оскільки 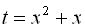 , то дістаємо
, то дістаємо 
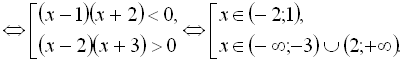




 .
.
Відповідь: 


 .
.






