Альтернативой способам решения СЛАУ, показанным выше, является применение встроенной функции lsolve (листинг 6). Для этого система уравнений должна быть записана в матричной форме AX=B.
Функция lsolve(A,B) возвращает вектор решения системы линейных алгебраических уравнений, имеющей матрицу коэффициентов А и вектор свободных членов В.
Функция lsolve не требует присвоения начальных значений вектору X, потому что в ней запрограммирован прямой численный метод, основанный на методе исключений Гаусса.
| Листинг 6. Использование встроенной функции lsolve |
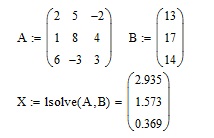
|
Во всех четырех примерах решалась одна и та же СЛАУ третьего порядка. Как видно из листингов, во всех случаях получен один и тот же реультат.
Важное замечание, касающееся работы в целом в приложении Mathcad.
По умолчанию вычисления в документе производятся в режиме реального времени, т. е. как только пользователь вводит в формулу оператор численного или символьного равенства, Mathcad пытается вычислить это выражение и все остальные формулы, находящиеся правее и ниже по тексту.
2.5. Контрольные вопросы
1) Как называются два этапа метода Гаусса решения СЛАУ? В чем состоит цель первого этапа, второго этапа?
2) К какому виду приводится матрица коэффициентов системы при выполнении прямого хода?
3) Для чего выполняется и в чем состоит процедура «выбора главного элемента»?
4) В чем состоит идея применения метода Гаусса при вычислении определителей?
5) Как влияет процедура «выбора главного элемента» на окончательное значение определителя?
6) Дайте определение массива.
7) С какого числа в Mathcad по умолчанию начинается нумерация элементов в массивах?
8) Как соотносятся между собой матрица и обратная к ней?
9) С помощью какого матричного соотношения можно найти вектор решений системы линейных алгебраических уравнений? Опишите все составляющие этого соотношения.
2.6. Таблица индивидуальных вариантов
| Подгруппа 1 | Подгруппа 2 | |||||||||||
| № вар. | Матрица А | Вектор В | № вар. | Матрица А | Вектор В | |||||||
| -2 | -6 | -3 | -3 | -2 | -6 | |||||||
| -7 | -7 | |||||||||||
| -6 | -6 | |||||||||||
| -5 | -5 | |||||||||||
| -4 | -4 | |||||||||||
| -8 | -1 | -6 | -6 | -8 | -1 | |||||||
| -15 | -15 | |||||||||||
| -3 | -2 | -5 | -5 | -3 | -2 | |||||||
| -9 | -9 | |||||||||||
| -3 | -5 | -9 | -9 | -3 | -5 | |||||||
| -1 | -1 | |||||||||||
| -3 | -3 | |||||||||||
| -7 | -7 | |||||||||||
| -2 | -4 | -2 | -4 | |||||||||
| -2 | -4 | -4 | -2 | |||||||||
| -5 | -5 | |||||||||||
| -4 | ||||||||||||
| -5 | -8 | -2 | -9 | -7 | -2 | -7 | -8 | -5 | -29 | |||
| -6 | -3 | -6 | -43 | |||||||||
| -4 | -5 | -5 | -4 | |||||||||
| -9 | -9 | |||||||||||
| -3 | -73 | |||||||||||
| -1 | -1 | |||||||||||
| -3 | -2 | -2 | -3 | |||||||||
| -1 | -9 | -1 | -19 | |||||||||
| -13 | -5 | -4 | -4 | -13 | -55 | |||||||
| -4 | -1 | -8 | -4 | -8 | -41 | |||||||
| -3 | -5 | -5 | -53 | |||||||||
| -3 | -4 | -3 | -47 | |||||||||
| -7 | -15 | -7 | -15 | |||||||||
| -9 | -11 | -11 | -1 | |||||||||
| -4 | -4 | |||||||||||
| -2 | -2 | |||||||||||
| -4 | -1 | -4 | -8 | |||||||||
| -4 | -3 | |||||||||||
| -5 | -43 | |||||||||||
| -2 | -6 | -3 | ||||||||||
| -1 | -9 | -1 | ||||||||||
| -5 | -3 | -9 | -5 | -10 | ||||||||
| -3 | -5 | |||||||||||
| -3 | -4 | |||||||||||
| -13 | -5 | -4 | -13 | |||||||||
| -1 | -9 | -11 | -1 | -37 | ||||||||
| -4 | -2 | -2 | ||||||||||
| -5 | -5 | |||||||||||
| -43 | ||||||||||||
| -7 | -1 | |||||||||||
| -11 | -3 | -7 | ||||||||||
| -4 | -7 | |||||||||||
| -2 | -2 |






