Мех 1,2
Содержание дисциплины по модулям
- Дифференциальное исчисление функций нескольких переменных.
- Кратные и криволинейные интегралы.
- Обыкновенные дифференциальные уравнения.
- Числовые, функциональные и тригонометрические ряды.
СРС 1 семестр
КОНСПЕКТ
ФНП. Определение, область определения. Предел, непрерывность.
Наибольшее и наименьшее значения функции 2-х переменных в замкнутой области.
Замена переменных в двойном интеграле.
Комплексные числа. Определение. Арифметические операции. Решение уравнений.
????
ТЕМЫ ДЛЯ ДОКЛАДОВ
— ВЫЧИСЛЕНИЯ В EXCEL, MATНCAD (LAB) и т.д.
| № | Дата (условно) | ЛЕКЦИИ |
| 1. | 30.01 | Модуль 6. Дифференциальное исчисление функций нескольких переменных Частные производные. Дифференциал. Производные высших порядков. |
| 2. | 06.02 | Дифференцирование сложной функции, неявно заданной функции. Частные производные высших порядков. |
| 3. | 07.02 | Производная по направлению. Градиент. Экстремум функции нескольких переменных. Нахождение наибольшего и наименьшего значений функции непрерывной в замкнутой ограниченной области. (Проверяем примеры на ЧП) |
| 4. | 13.02 | Модуль 7. Кратные и криволинейные интегралы. Двойной интеграл. Определение. Свойства двойного интеграла |
| 5. | 20.02 | Вычисление двойного интеграла в декартовой системе координат. |
| 6. | 21.02 | Вычисление двойного интеграла полярной системе координат. |
| 7. | 27.02 | Приложения двойного интеграла. |
| 8. | 06.03 | Криволинейный интеграл I-го рода, свойства и вычисление.??? |
| 9. | 07.03 | Криволинейный интеграл II-го рода, свойства и вычисление. |
| 10. | 13.03 | Модуль 8. Обыкновенные дифференциальные уравнения Обыкновенные дифференциальные уравнения. Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. |
| 11. | 20.03 | Уравнения с разделяющимися переменными, линейные уравнения и уравнения Бернулли. |
| 12. | 21.03 | Линейные однородные и неоднородные ДУ высших порядков.Фундаментальная система решений. Теоремы о структуре общего решения этих уравнений |
| 13. | 27.03 | Метод Лагранжа вариации произвольных постоянных. |
| 14. | 04.04 | Комплексные числа. |
| 15. | 05.04 | Линейные однородные ДУ с постоянными коэффициентами. |
| 16. | 11.04 | Структура общего решения линейных неоднородных уравнений с постоянными коэффициентами. Метод Лагранжа отыскания частного решения линейного неоднородного уравнения. |
| 17. | 18.04 | Уравнения со стандартной правой частью. |
| 18. | 19.04 | Модуль 9. Числовые, функциональные и тригонометрические рядыЧисловые ряды. Сходимость и сумма ряда. Необходимое условие сходимости рядов. |
| 19. | 25.04 | Достаточные признаки сходимости знакоположительных рядов. |
| 20. | 02.05 | Знакочередующиеся и знакопеременные ряды. Теорема Лейбница. |
| 21. | 03.05 | Функциональные ряды. Область сходимости. Степенные ряды. Теорема Абеля. Свойства степенных рядов. |
| 22. | 09.05 | Ряды Тейлора и Маклорена. Разложение функций в степенные ряды. |
| 23. | 16.05 | Приложения степенных рядов. |
| 24. | 17.05 | Тригонометрические ряды Фурье. |
| 23.05 | Разложение функций в тригонометрические ряды Фурье. | |
| 29.05 | Обзорная лекция |
Семестр. ПРАКТИКИ
| 1. | Модуль 6. Дифференциальное исчисление функций нескольких переменных Частные производные. Частные производные высших порядков. |
| 2. | Дифференцирование сложной функции, неявно заданной функции. Частные производные высших порядков. |
| 3. | Производная по направлению. Градиент. |
| 4. | Локальный экстремум функции нескольких переменных. КР |
| 5. | Модуль 7. Кратные и криволинейные интегралы Вычисление двойного интеграла в ДСК |
| 6. | Вычисление двойного интеграла в ПСК |
| 7. | Приложения двойного интеграла. |
| 8. | КР |
| 9. | Модуль 8. Обыкновенные дифференциальные уравнения Уравнения с разделяющимися переменными, линейные, Бернулли. |
| 10. | Линейные однородные уравнения с постоянными коэффициентами. |
| 11. | Метод Лагранжа (вариации) отыскания частного решения линейного неоднородного уравнения. |
| 12. | Уравнения со стандартной правой частью. |
| 13. | КР |
| 14. | Модуль 9. Числовые, функциональные и тригонометрические ряды Числовые ряды. Необходимое условие сходимости. Достаточные признаки сходимости знакоположительных рядов. |
| 15. | Знакочередующиеся ряды. |
| 16. | Степенные ряды. Область сходимости, приложения |
| 17. | Тригонометрические ряды Фурье. |
| 18. | КР |
Контрольные работы (примеры для подготовки к экзамену)
ФНП
Изобразить область определения функции
 , , 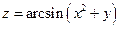
|
Найти частные производные первого порядка функции
1) 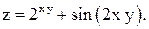 2) 2)  3) 3) 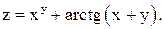
|
Исследовать функцию на экстремум.
1) 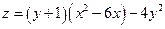 2) 2) 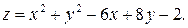 3)
3) 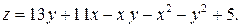 4) 4) 
|
Найти наибольшее и наименьшее значения функции в замкнутой области СРС!!!
1) 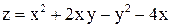 в треугольнике со сторонами в треугольнике со сторонами 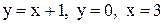 .
2) .
2) 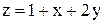 в области, ограниченной прямыми в области, ограниченной прямыми  3)
3)  в треугольнике со сторонами в треугольнике со сторонами  4)
4)  в квадрате в квадрате 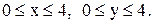
|
Найти производную функции в точке по направлению
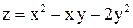 в точке (1; 2) в направлении, составляющем с осью OX угол в 60о. в точке (1; 2) в направлении, составляющем с осью OX угол в 60о.
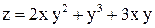 в точке (4; 1) в направлении от этой точки к точке (5; 1). в точке (4; 1) в направлении от этой точки к точке (5; 1).
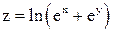 в точке (1; 1) в направлении биссектрисы 1-го координатного угла. в точке (1; 1) в направлении биссектрисы 1-го координатного угла.
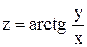 в точке (1; 3) по направлению вектора в точке (1; 3) по направлению вектора 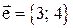 . .
|






