Чтобы определить температуру внутри тела в любой момент времени, недостаточно одного уравнения (6). Необходимо, как следует из физических соображений, знать еще распределение температуры внутри тела в начальный момент времени (начальное условие) и тепловой режим на границе тела (граничное условие).
Начальное условие в отличие от уравнения гиперболического типа задается только одно, т.к. исходное уравнение содержит лишь первую производную по времени.
Граничные или краевые условия могут быть различны в зависимости от температурного режима на границе тела. Основными видами тепловых режимов являются следующие: I – на границе поддерживается определенная температура; II – на границу подается определенный тепловой поток; III – происходит теплообмен с внешней средой, температура которой известна. Им соответствуют граничные условия первого, второго, третьего рода.
Сформулируем прежде условия для одномерного уравнения теплопроводности.
Начальное условие состоит в задании функции u = u (x, t) в начальный момент времени (t = 0):
u (x,0) = 
(10)
Выведем граничные условия в случаях I – III.
1. На концах стержня (или на одном конце) задается температура
(t) (11)
где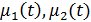 
- функции, заданные в некотором промежутке 
причем T есть промежуток времени, в течении которого изучается процесс. В частности,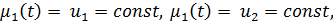 
т.е. на концах поддерживается постоянная температура 
и 
.
2. На одном из концов (или на обоих) задано значение производной искомой функции. Например, для сечения x = 0
(12)
Дадим физическое толкование этому условию. Пусть 
t) – величина теплового потока, т.е. количество тепла, протекающего через торцевое сечение x = 0 в единицу времени. Тогда уравнение теплового баланса для элемента стержня (0; Δx) в период времени 
t, как и при выводе уравнения (4) запишется в виде
Сократив на Δt и перейдя к пределу при Δx 
0, получим 
Таким образом, имеем условие (12), в котором 
известная функция выражающаяся через заданный поток тепла 
по формуле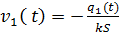 
Аналогично для сечения x = 1 через которое протекает количество тепла 
, найдем 
Следовательно, условие или 
имеет место вслучае, когда на соответствующем конце стержня задан тепловой поток, втекающий или вытекающий. В частности, если концевое сечениетеплоизолировано, то 
(t) = 0 или 
(t) = 0, и следовательно,
= 0 или 
3. На одном из концов (или на обоих) задается линейное соотношение между функцией и ее производной. Например, для сечения x = l
(13)
Условие типа (13) используется в случае процесса теплоотдачи, т.е. переноса тепла от тела к окружающей среде. Закон теплообмена сложен; но для упрощения задачи он может быть принят в виде закона Ньютона. Согласно эмпирическому закону Ньютона количество тепла, отдаваемого в единицу времени с единицы площади поверхности тела в окружающую среду, температура 
которой известна, пропорционально разности температур поверхности тела и окружающей среды:
q =α(u –θ),
где α - коэффициент теплообмена (или внешней теплопроводности).
Можно определить тепловой поток через сечение стержня, воспользовавшись двумя выражениями в cилу закона сохранения энергии.
Согласно закону Ньютона тепловой поток q(t), вытекающий через сечение
x = l, равен
q =α(u(l, t) –θ(t)).
С другой стороны, такой же тепловой поток должен подводиться изнутри путем теплопроводности. Поэтому согласно закону Фурье
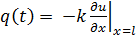
Приравнивая правые части этих выражений, найдем
Отсюда получаем математическую формулировку условия в виде 
, 
.
Заметим, что граничные условия, наложенные на значения функции u (x t), называют условиями первого рода. Граничные условия, наложенные на значение производной 
называют условиями второго рода. А условия, наложенные как на значение функции u (x, t), так и на значение производной 
, называют условиями третьего рода.
В случае граничных условий вида (11), (12), (13) говорят соответственно о первой, второй, третьей краевых задачах для уравнения теплопроводности. Начальное условие для всех указанных краевых задач остается тем же самым и дается равенством (10).
Так, первая краевая задача состоит в отыскании решения u = u (x, t) уравнения
при 0<x< l, 0<t 
T
удовлетворяющего условиям
u(x,0) = 
0<x< l,
u(0, t) = 
, 0<t T
Аналогично ставятся другие краевые задачи с различными комбинациями граничных условий при x = 0 и x = l.
