ВВЕДЕНИЕ
Уравнение диффузии или уравнение теплопроводности представляет собой частный вид дифференциального уравнения в частных производных. Бывает нестационарным и стационарным.
Математически уравнение диффузии и уравнение теплопроводности не различаются, и применение того или иного названия ограничено только конкретным приложением, причем второе представляется более частным, так как можно говорить, что в этом случае речь идет о диффузии тепловой энергии.
В смысле интерпретации при решении уравнения диффузии речь идет о нахождении зависимости концентрации вещества (или иных объектов) от пространственных координат и времени, причем задан коэффициент (в общем случае также зависящий от пространственных координат и времени), характеризующий проницаемость среды для диффузии. При решении уравнения теплопроводности речь идет о нахождении зависимости температуры среды от пространственных координат и времени, причем задана теплоемкость и теплопроводность среды (также в общем случае неоднородной).
Физически в том и другом случае предполагается отсутствие или пренебрежимость макроскопических потоков вещества. Таковы физические рамки применимости этих уравнений. Также, представляя непрерывный предел указанных задач (то есть не более, чем некоторое приближение), уравнение диффузии и теплопроводности в общем не описывают статистических флуктуаций и процессов, близких по масштабу к длине и времени свободного пробега, также весьма сильно отклоняясь от предполагаемого точного решения задачи в том, что касается корреляций на расстояниях, сравнимых (и больших) с расстояниями, проходимыми звуком (или свободными от сопротивления среды частицами при их характерных скоростях) в данной среде за рассматриваемое время.
Это в подавляющей части случаев сразу же означает и то, что уравнения диффузии и теплопроводности по области применимости далеки от тех областей, где становятся существенными квантовые эффекты или конечность
скорости света, то есть в подавляющей части случаев не только по своему выводу, но и принципиально, ограничиваются областью классической ньютоновской физики.
Уравнение параболического типа. Основные уравнения
Уравнения параболического типа наиболее часто встречаются при изучении процессов теплопроводности и диффузии. К этим уравнениям приводятся также задачи о движении вязкой жидкости, например, нефти.
Обсудим процесс распространения тепла в неравномерно нагретом твердом теле. Если тело нагрето неравномерно, то в нем происходит передача тепла из мест с более высокой температурой в места с более низкой температурой. Процесс может быть описан функцией u = u (x, y, z, t) дающей температуру u в каждой точке M (x, y, z) тела и в любой момент времени t.
Примем следующую модель процесса: происходит механический перенос тепла от более нагретых частей тела к менее нагретым; все тепло идет на изменение температуры тела; свойства тела от температуры не зависят. Идеализация явления состоит в том, что мы будем изучать процесс, не касаясь его молекулярной природы, а также иных проявлений. Опишем процесс математически для одномерного тела.
Вывод уравнения теплопроводности для одномерного случая
Рассмотрим однородный стержень длины l, теплоизолированный с боков (через поверхность не происходит теплообмена с окружающей средой) и достаточно тонкий, чтобы в любой момент времени температуру во всех точках поперечного сечения можно было считать одинаковой. Расположим ось Ox так, чтобы один конец стержня совпадал с точкой x = 0, а другой - с точкой x = l (рис. 1).
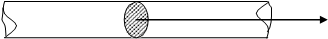
Рисунок - 1
Чтобы найти функцию u=u(x, t), надо составить дифференциальное уравнение, которому она удовлетворяет.
При выводе дифференциального уравнения теплопроводности воспользуемся следующими физическими закономерностями, связанными с распространением тепла.
1. Количество тепла DQ, которое необходимо сообщить однородному телу, чтобы повысить его температуру на Du, равно
ΔQ = cmΔu,
где c - удельная теплоемкость, m - масса тела.
Для стержня имеем
ΔQ = cρSΔxΔu, (1)
где ρ - плотность материала стержня; S - площадь его поперечного сечения.
2. Перенос тепла в теле подчиняется эмпирическому закону Фурье количество тепла ΔQ, протекающее за время Δt через площадку ΔS в направлении нормали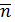 
к этой площадке, равно
где k - коэффициент внутренней теплопроводности (зависит от точки и не зависит от направления, если тело изотропно).
Для стержня имеем
, (2)
где коэффициент k будем считать постоянным в силу предположения о его однородности. Если стержень неоднороден, то k = k(x).
3. Если внутри тела есть источники тепла, то выделение тепла можно характеризовать плотностью тепловых источников, т.е. количеством выделяемого (или поглощаемого) тепла в единицу времени в единице объема.
Обозначим через F (x, t), плотность источников в точке x рассматриваемого стержня в момент t. Тогда в результате действия этих источников на участке (x, x +Δx) за промежуток Δt будет выделено количество тепла
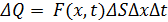(3)
И, наконец, воспользуемся законом сохранения энергии.
Итак, приступим к выводу уравнения. Выделим элементарный участок стержня, заключенный между сечениями x = x1 и x = x2 (x2 - x1 = Δx), и составим уравнение теплового баланса на отрезке [x1, x2]. Так как боковая поверхность стержня теплоизолирована, то элемент стержня может получать тепло только через поперечные сечения. Согласно (2) количество тепла, прошедшее через сечение x = x1, равно
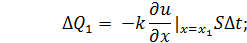
через сечение x = x2:
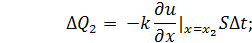
Найдем приток тепла 
в элемент стержня: 
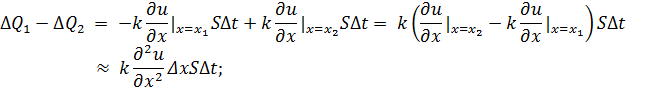
(К разности частных производных применена теорема Лагранжа).
Кроме того, в результате действия внутренних источников тепла на этом участке в течение времени Δt выделится количество тепла согласно (3)
Все тепло за время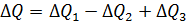 
Δt пойдет на изменение температуры выделенного элемента стержня на величину Δu.И поэтому сообщенное количество тепла ΔQ, с другой стороны, может быть найдено согласно формуле (1):
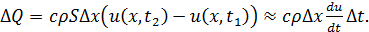
В силу закона сохранения энергии имеем равенство
Сокращая на общий множитель SΔxΔt, получим уравнение
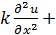
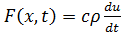
Введя обозначения 
, 
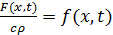придем к уравнению
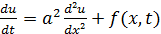(4)
Это и есть искомое дифференциальное уравнение распространения тепла в однородном стержне. Уравнение (4) называют уравнением теплопроводности, в котором постоянную a² температуропроводности. Коэффициент a² называют коэффициентом имеет размерность м² /с.
Уравнение (4) является линейным неоднородным уравнением параболического типа.
Вывод дифференциального уравнения распространения тепла внутри тела, отнесенного к пространственной системе координат, основан на тех же физических законах. Поэтому, ограничившись выводом уравнения для простейшего случая – одномерного, лишь приведем уравнение для трехмерного пространства.
Процесс распределения температуры u = u (x, y, z, t) в изотропном теле описывается уравнением
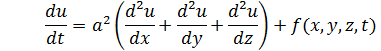
которое кратко записывается так:
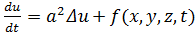(6)
где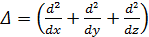 
- оператор Лаплас
