Основна модель. Найважливішу роль у наших розглядах відіграватиме функція зміни запасів. Це зв'язок між кількістю одиниць товару на складі (потначимо його через Q) і часом t. Вважатимемо, що маємо один вид товару.
Якщо на товар є попит, то функція зміни запасу Q = Q(t) зменшується. Якщо товар, навпаки, завозять на склад, то ця функція зростає. Вважатимемо за можливе миттєве поповнення запасу.
Витрати, що пов'язані із запасами, можна розділити на три частини:
A. Вартість товару.
Б. Організаційні витрати. Це - витрати, пов'язані з оформленням товару, його доставкою, розвантаженням тощо.
В. Витрати на збереження товару. Це - витрати на оренду складу, амортизацію в процесі збереження тощо.
Розглянемо основні величини і припущення відносно них, прийняті в рамках основної моделі. Використовуватимемо як одиницю виміру коштів умовні одиниці (УО); як одиницю виміру часу - рік, хоча можна було б узяти місяць, квартал тощо.
1. Ціна одиниці товару - с. Ціна постійна, розглядається один вид товару.
2. Інтенсивність попиту - d одиниць товару в рік.
3. Організаційні витрати - s за одну партію товару. Вважатимемо, що організаційні витрати не залежать від розміру постачання, тобто від кількості одиниць товару в одній партії.
4. Витрати на збереження запасу - h на одиницю товару в рік. Вважатимемо ці витрати постійними.
5. Розмір однієї партії товару є постійний - q одиниць. Партія надходить миттєво в той момент, коли виникає дефіцит, тобто коли запаси на складі дорівнюють нулю.
Параметри с, d, s, h вважаються заданими і потрібно. Задача управління запасами складається у виборі параметра q в такий спосіб, щоб мінімізувати річні витрати.
Отже, загальні витрати С обчислюються за формулою:
.
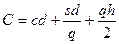Ще раз нагадаємо, що в рамках моделі параметри с, d, s, h вважаються заданими і потрібно знайти таке число q*, щоб функція С=С(q) приймала найменше значення на безлічі q >0 саме в точці q*:
.
Отримана формула називається формулою оптимального запасу, чи формулою Харріса.
Знайшовши оптимальний розмір замовлення, можна визначити оптимальну кількість постачань за рік п* і відповідну тривалість циклу зміни запасу t*:
; 
днів.
Метод виробничих постачань. В основній моделі передбачалося, що надходження товарів на склад відбувається миттєво. Це припущення достатньо добре відображає ситуацію, коли товар поставляється протягом одного дня (чи ночі). Якщо товари поставляються з працююча виробничої лінії, необхідно модифікувати основну модель. У цьому разі до параметрів с, d, s, h додається ще один - продуктивність виробничої лінії р (одиниць товару в рік). Вважатимемо її заданою і постійною.
Ця нова модель називається моделлю виробничих постачань. Величина q, як і раніше, позначає розмір партії. На початку кожного циклу відбувається "підключення" лінії, що продовжується до нагромадження у одиниць товару. Після цього поповнення не відбувається доти, поки не виник дефіцит.
Загальні витрати С(q), як і в основній моделі, складаються з трьох частин та обчислюються за формулою:
.
Оптимальний розмір постачань q * одержуємо з рівняння:
.
Знайшовши оптимальний розмір замовлення, можна визначити оптимальну кількість постачань за рік п* і відповідні тривалість постачання τ* і тривалість циклу поповнення запасу t *:
; 
днів; 
день.
Метод постачань зі знижкою. Розглянемо ситуацію, описувану в цілому основною моделлю, але з однією особливістю, що полягає в тому, що товар можна поставляти за пільговою ціною (зі знижкою), якщо розмір партії досить великий. Іншими словами, якщо розмір партії q є не менший від заданого числа qо, товар поставляється за ціною со, де со < с.
Функція загальних витрат С(q) задається в такому випадку у спосіб:
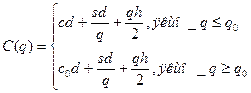
Обидві функції мають мінімум у точці, де 
.
Для з'ясування питання про те, який розмір партії оптимальний, варто порівняти значення функції С(q) у точці 
і 
та точка, де функція С(q) приймає менше значення, буде оптимальним розміром партії 
у моделі постачань зі знижкою.
Методи розподілу ресурсів
Мається п Споживачів, кожний з який заявляє Центру число si (i = 1,2,..... п) – заявку, а також ще деяку інформацію. Далі Центр на підставі заявок Споживачів, що мається в його розпорядженні ресурсу R и додаткової інформації про Споживачів обчислює за деяким правилом числа xi (i = 1,2..... п) - обсяг ресурсу, що виділяється і-му Споживачу.
У випадку
(відсутність дефіциту) природним рішенням Центра є наступне:
хі=si
(кожен Споживач одержує стільки, скільки просив). Надалі ми будемо вважати виконаним нерівність
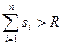
(сумарна заявка Споживачів перевершує ресурс Центра).
Відзначимо наступне важливу обставину. Споживачі формують свої заявки на підставі власних реальних потреб ri що їм відомі, але невідомі Центру. Можна сказати. що числа si є стратегіями Споживачів як учасників ієрархічної гри. У свою чергу, стратегією Центра є числа хi.
Метод прямих пріоритетів. Метод прямих пріоритетів відноситься до числа так званих пріоритетних механізмів, відмітною рисою яких є приписування кожному Споживачу деякого пріоритету. Отже, поряд з розмірами заявок si (і = 1, 2, … п) Центр враховує пріоритет кожного Споживача, що визначається числом Ai, (і = 1, 2, … п).
Відповідно до механізму прямих пріоритетів розподіл ресурсу здійснюється за правилом
xi = min{si, yAisi}, i= 1,2,...,п, (1)
де y - загальний для всіх Споживачів параметр - визначається з умови
(2)
(весь ресурс розподіляється без залишку).
Особливо простий вигляд формула (1) здобуває у випадку "рівності" Споживачів з погляду Центра, тобто при
А1 = А2 = … = Ап = 1
Тоді
xi = min{si, ysi}=ysі, i= 1,2,...,п,
(випадок хі=si неможливий, оскільки при цьому кожен Споживач одержує стільки, скільки просив, а це суперечить умові про наявність дефіциту). З умови (2) одержуємо
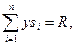
звідки
Метод зворотних пріоритетів. Механізм зворотних пріоритетів ґрунтується на припущенні, що, чим менше потрібно Споживачу ресурсу, тим більше ефективність його використання. Відповідно до цього розподіл ресурсу здійснюється за правилом
xi = min{si, yAi /si}, i= 1,2,...,п, (3)
де число у визначається, як і в механізмі прямих пріоритетів, з умови
З формули (3) видно, що подаючи дуже малу або дуже велику заявку si,. Споживач одержує малий ресурс хі.
Знайдемо, яку ж заявку si, повинний подавати і-й Споживач, щоб одержати максимальний ресурс хі (в умовах дефіциту така ціль Споживача представляється цілком зрозумілою).
Максимальне значення s*i розраховується так
Таким чином, рівноважним є набір стратегій Споживачів
… 
при цьому
хі= s*i
Вибираючи замість s*i будь-яку іншу стратегію si і-й Споживач лише зменшує виділюваний йому ресурс х і,.
Залишилося обчислити константу у. Маємо:
звідки
.
Зауваження. Ще раз відзначимо, що набір стратегій s*i (i = 1,2,..... п) є рівноважним, тобто, подаючи будь-яку заявку 
і-й Споживач лише зменшує виділюваний йому ресурс хі. Можна довести, що кожна зі стратегій s*i є також гарантуючої, тобто у випадку застосування і-м Споживачем цієї стратегії він у будь-якому випадку (тобто при будь-яких заявках інших Споживачів) одержує не менше, ніж х і = s*i.
Зауваження 1. Через помилки округлення сума заявок небагато відрізняється від R=60.
Зауваження 2. Насправді ми розглянули випадок, коли s*i < r i, для всіх i, тобто коли кожний iз Споживачів змушений, подаючи заявку, занижувати свою реальну потребу. Може бути і так. що для деяких Споживачів s*i ≥ r i,. тоді ці Споживачі подають заявку на ресурс si = r i, і стільки ж одержують.
Метод конкурсного механізму. Конкурсний механізм застосовується в тих випадках, коли недоцільно "урізати” заявки, оскільки Споживачам ресурс потрібний на реалізацію яких-небудь конкретних проектів, на які меншого ресурсу не вистачить. У цих умовах Центр проводить конкурс заявок. Ті, хто перемагають у конкурсі, цілком одержують необхідний ресурс, а програвши не одержують нічого.
Реалізація цього відбувається в такий спосіб. Споживачі повідомляють Центру свої заявки si, а також величини wi, що характеризують ефект, що вони мають намір одержати. На підставі цих даних Центр обчислює для кожного Споживача показник ефективності (ei):
Після цей ресурс розподіляється в такий спосіб. Спочатку розглядається Споживач з найбільшою ефективністю. Йому виділяється стільки, скільки він просить (якщо в Центра вистачає ресурсу). Потім береться другий по ефективності і т.д.. У якийсь момент виявляється, що на задоволення чергової заявки ресурсу, що залишився в Центра, не вистачає. Тоді цей споживач, так само як і всі що залишилися, нічого не одержує.
Зауваження. В ефективності описаного механізму можуть виникнути сумніву. Адже Споживачі можуть пообіцяти великий ефект, одержати ресурс, а потім не виконати обіцяного. Тому при реальному застосуванні конкурсного механізму необхідна діюча система контролю (можливо, поетапний контроль для проектів із тривалим часом реалізації).
Метод відкритого управління. В усіх розглянутих вище методах розподілу ресурсів Споживачі можуть домогтися кращого для себе рішення Центра шляхом перекручування інформації. У такий спосіб, Центр не одержує достовірних даних про запити Споживачів.
Можливість ефективно керувати на підставі недостовірної інформації представляється, узагалі говорячи, сумнівною. Тому цікаві методи відкритого управління, ідея яких полягає в створенні для Споживачів стимулів до повідомлення в заявці своїх реальних потреб.
4. Варіанти індивідуальних завдань
Варіант 1.
1. Одноканальна система масового обслуговування (СМО) являє собою одну телефонну лінію. Заявка — виклик, що прийшла в момент зайнятої лінії, одержує відмовлення. Потік викликів надходить з інтенсивністю λ=2 (викликів за хвилину). Середня тривалість розмови tоб=3 хв. Усі потоки подій найпростіші. Потрібно визначити граничні значення: 
1) відносної пропускної здатності q;
2) абсолютної пропускної здатності А;
3) ймовірності відмовлення Рвдм.
2. Система управління запасами описується моделлю виробничих постачань і має наступні значення параметрів. Попит дорівнює 1,5 тис. одиниць у рік, ціна 2 дол., витрати збереження одиниці товару протягом року - 0,2 дол., організаційні витрати -10 дол. Протягом року може бути зроблено 4,5 тис. одиниць товару при повному завантаженні виробничої лінії.
3. Система управління запасами деякого виду товару підкоряється умовам основної моделі. Щороку з постійною інтенсивністю надходить попит на 15 тис. одиниць товару, витрати на організацію постачання складають 10 дол. за одну партію, ціна одиниці товару - 3 дол.. а витрати на її збереження - 0,75 дол. у рік. Знайдіть оптимальний розмір партії.
Варіант 2.
1. Трьохканальна система масового обслуговування (СМО) являє собою одну телефонну лінію. Заявка — виклик, що прийшла в момент зайнятої лінії, одержує відмовлення. Потік викликів надходить з інтенсивністю λ=1,2 (викликів за хвилину). Середня тривалість розмови tоб=2,5 хв. Усі потоки подій найпростіші. Потрібно визначити граничні значення:
1) відносної пропускної здатності q;
2) абсолютної пропускної здатності А;
3) ймовірності відмовлення Рвдм.
2. Інтенсивність попиту в моделі виробничих постачань складає чверть швидкості виробництва, що дорівнює 20 тис. одиниць товару в рік. Організаційні витрати для однієї партії рівні 150 дол., а витрати збереження одиниці товару протягом року - 0,3 дол. Визначте оптимальний розмір партії.
3. Припустимо, що інтенсивність рівномірного попиту складає 1000 одиниць товару в рік. Організаційні витрати рівні 10 УЕ, витрати на збереження - 4 УЕ. Ціна одиниці товару дорівнює 5 УЕ, однак, якщо розмір партії не менш 500 одиниць, ціна знижується до 4 УЕ. Знайти оптимальний розмір партії.
Варіант 3.
1. Торгове підприємство, що обслуговує покупців по телефонних замовленнях, оперує п'ятьма операторами з телефонами для прийому заявок (п= 4 операторів). Замовлення на товари надходять у випадкові моменти часу незалежно один від одного, в середньому два замовлення за хвилину (λ=3 замовлення). Середній час обслуговування покупця складає одну хвилину (tоб=1,5).
Необхідно розрахувати:
1) Ймовірність того, що в будь-який момент часу всі оператори виявляться вільними (Рв). 2) Середньоочікувана кількість вільних операторів (Nв). 3) Ймовірність того, що в покупця, що подзвонив, не буде кому прийняти замовлення, тому що всі оператори виявляться зайнятими (Рз). 4) Середньоочікуване число зайнятих операторів (Nз). 5) Коефіцієнт простою операторів за час обслуговування (Кп). 6) Частка завантажених операторів за час обслуговування (Кз).
2. Меблевій фірмі потрібно 1000 штук дверних ручок у рік, що витрачаються з постійною інтенсивністю. Організаційні витрати складають 30 дол. за партію, витрати на збереження однієї ручки оцінені в 1 дол. Ціна дверної ручки складає 2 дол., а при закупівлі партіями обсягом не менш 750 штук - 1,9 дол. за штуку. Знайдіть оптимальний розмір партії постачань.
3. Інтенсивність рівномірного попиту складає 1 тис. одиниць товару в рік. Товар поставляється з конвеєра, продуктивність якого складає 5 тис. одиниць у рік. Організаційні витрати рівні 10 УЕ, витрати на збереження - 2 УЕ, ціна одиниці товару - 5 УЕ. Чому дорівнює оптимальний розмір партії?
Варіант 4.
1. При будівництві моста довжиною 900 м через ріку витрачаються спеціальні тяжі (ванти) з міцної сталі вагою 230 кг/м. Термін спорудження моста — 900 діб. Витрата тяжів - рівномірна. Вартість рейсу, що включає вантажно-розвантажувальні роботи, не залежить від числа доставлених тяжів і дорівнює 20 тис. грн. Витрати на зберігання тяжів зумовлені зведенням приоб'єктного складу, його експлуатацією і втратами при збереженні. Вони складають 2,5 тис. грн. за 1 т тяжів за добу.
Визначити оптимальні: партію постачання, інтервал поновлення замовлень, витрати роботи протягом періоду будівництва.
2. Торговець має стабільний попит на деякий товар у кількості 500 одиниць у рік. Товар він купує в постачальника за ціною б дол. за штуку, причому витрати на оформлення постачання й інші підготовчі операції складають у кожнім випадку 10 дол. Якщо торговець купує відразу партію в кількості 150 одиниць товару чи більше, ціна зменшується до 5 дол. за штуку. Який оптимальний розмір партії, якщо річні витрати на збереження одиниці товару рівні 1 дол.?
3. Попит на нестандартну продукцію складає 2900 одиниць у рік. Вартість збереження, включаючи втрати від нерухомості засобів у запасах і зв'язані зі зниженням цін при нереалізації продукції, дорівнює 29 тис. грн. за одиницю в рік. Витрати розміщення замовлення не перевищують 45 тис. грн. Незадоволені вимоги беруться на облік. Питомі витрати дефіциту — 71 тис. грн. за недостачу одиниці продукції протягом року.
Треба визначити оптимальну партію постачання, максимальну величину заборгованого попиту, інтервал поновлені постачання, місце розміщення замовлення (
= 1 місяць = 1/12 року) і річні втрати функціонування системи.
Варіант 5.
1. Завод випускає різні типи лакофарбових матеріалів партіями на тому самому устаткуванні. При переході від одного виду матеріалів до іншого приходиться нести витрати від переналагоджень устаткування в середньому на рівні 400 тис. грн. Середня потреба в матеріалах кожного типу — 5000 т у рік. Вартість 1т — 260 тис. грн. Витрати на зберігання — 12% від вартості продукції, що пролежала.
Потрібно знайти оптимальну партію запуску виробу у виробництво, його періодичність і середньорічні витрати роботи системи.
2. Нехай інтенсивність рівномірного попиту складає 1000 одиниць товару в рік. Організаційні витрати рівні 10 УЕ, витрати на збереження - 4 УЕ на одиницю товару в рік, ціна товару - 5 УЕ.
Визначити оптимальний розмір партії в припущенні, що система підпорядковується основній моделі.
3. Середня потреба машинобудівного заводу в чавунних заготівлях — 11 тис. у рік. Витрати розміщення замовлення — 25 тис. грн., зберігання однієї заготівлі — 3 тис. грн. у рік. Середній час реалізації замовлення — 20 днів.
Визначити оптимальну партію постачання, періодичність поновлення постачань, місце розміщення замовлення, мінімальний початковий запас і моменти повторення замовлень.
Варіант 6.
1. Середня потреба машинобудівного заводу в чавунних заготівлях — 10 тис. у рік. Витрати розміщення замовлення — 15 тис. грн., зберігання однієї заготівлі — 3 тис. грн. у рік. Середній час реалізації замовлення — 15 днів.
Визначити оптимальну партію постачання, періодичність поновлення постачань, місце розміщення замовлення, мінімальний початковий запас і моменти повторення замовлень.
2. Нехай п'ять Споживачів подали заявки в розмірі 5, 8, 12, 7 і 8. Наявний у розпорядженні Центра ресурс складає 32. Як повинний бути розподілений цей ресурс відповідно до механізму прямих пріоритетів?
3. Завод випускає різні типи лакофарбових матеріалів партіями на тому самому устаткуванні. При переході від одного виду матеріалів до іншого приходиться нести витрати від переналагоджень устаткування в середньому на рівні 200 тис. грн. Середня потреба в матеріалах кожного типу — 1500 т у рік. Вартість 1т — 120 тис. грн. Витрати на зберігання — 5% від вартості продукції, що пролежала.
Потрібно знайти оптимальну партію запуску виробу у виробництво, його періодичність і середньорічні витрати роботи системи.
Варіант 7.
1. Попит на нестандартну продукцію складає 1500 одиниць у рік. Вартість збереження, включаючи втрати від нерухомості засобів у запасах і зв'язані зі зниженням цін при нереалізації продукції, дорівнює 20 тис. грн. за одиницю в рік. Витрати розміщення замовлення не перевищують 50 тис. грн. Незадоволені вимоги беруться на облік. Питомі витрати дефіциту — 20 тис. грн. за недостачу одиниці продукції протягом року.
Треба визначити оптимальну партію постачання, максимальну величину заборгованого попиту, інтервал поновлені постачання, місце розміщення замовлення ( = 1 місяць = 1/12 року) і річні втрати функціонування системи.
2. Нехай мається п'ять Споживачів, пріоритети яких визначаються числами 9, 5, 10, 13, 12. Ресурс Центра складає 60. Визначити рівноважні стратегії (заявки) Споживачів, якщо ресурс розподіляється відповідно до механізму зворотних пріоритетів.
3. При будівництві моста довжиною 700 м через ріку витрачаються спеціальні тяжі (ванти) з міцної сталі вагою 110 кг/м. Термін спорудження моста — 120 діб. Витрата тяжів - рівномірна. Вартість рейсу, що включає вантажно-розвантажувальні роботи, не залежить від числа доставлених тяжів і дорівнює 9 тис. грн. Витрати на зберігання тяжів зумовлені зведенням приоб'єктного складу, його експлуатацією і втратами при збереженні. Вони складають 1,2 тис. грн. за 1 т тяжів за добу.
Визначити оптимальні: партію постачання, інтервал поновлення замовлень, витрати роботи протягом періоду будівництва.
Варіант 8.
1. Інтенсивність рівномірного попиту складає 1 тис. одиниць товару в рік. Товар поставляється з конвеєра, продуктивність якого складає 5 тис. одиниць у рік. Організаційні витрати рівні 10 УЕ, витрати на збереження - 2 УЕ, ціна одиниці товару - 5 УЕ. Чому дорівнює оптимальний розмір партії?
2. Мається шість Споживачів, що подала заявки в розмірі 14, 18, 12, 16, 12, 14 і повідомили наступні показники ефекту: 26, 28, 15, 22, 18, 19. Яким повинно бути розподіл ресурсу обсягом 70 відповідно до конкурсного механізму?
3. Торгове підприємство, що обслуговує покупців по телефонних замовленнях, оперує п'ятьма операторами з телефонами для прийому заявок (п= 6 операторів). Замовлення на товари надходять у випадкові моменти часу незалежно один від одного, в середньому два замовлення за хвилину (λ=3 замовлення). Середній час обслуговування покупця складає одну хвилину (tоб=1).
Необхідно розрахувати:
1) Ймовірність того, що в будь-який момент часу всі оператори виявляться вільними (Рв). 2) Середньоочікувана кількість вільних операторів (Nв). 3) Ймовірність того, що в покупця, що подзвонив, не буде кому прийняти замовлення, тому що всі оператори виявляться зайнятими (Рз). 4) Середньоочікуване число зайнятих операторів (Nз). 5) Коефіцієнт простою операторів за час обслуговування (Кп). 6) Частка завантажених операторів за час обслуговування (Кз).
Варіант 9.
1. Припустимо, що інтенсивність рівномірного попиту складає 1000 одиниць товару в рік. Організаційні витрати рівні 9 УЕ, витрати на збереження - 4 УЕ. Ціна одиниці товару дорівнює 6 УЕ, однак, якщо розмір партії не менш 500 одиниць, ціна знижується до 5 УЕ. Знайти оптимальний розмір партії.
2. Вісім Споживачів подали Центру свої заявки. Вони такі: 12, 6, 6, 4, 5, 8, 10, 5. Центр має ресурс R = 50. Потрібно розподілити цей ресурс відповідно до методу відкритого управління.
3. Двохканальна система масового обслуговування (СМО) являє собою одну телефонну лінію. Заявка — виклик, що прийшла в момент зайнятої лінії, одержує відмовлення. Потік викликів надходить з інтенсивністю λ=1 (викликів за хвилину). Середня тривалість розмови tоб=2 хв. Усі потоки подій найпростіші. Потрібно визначити граничні значення:
1) відносної пропускної здатності q;
2) абсолютної пропускної здатності А;
3) ймовірності відмовлення Рвдм.
Варіант 10.
1. Система управління запасами деякого виду товару підкоряється умовам основної моделі. Щороку з постійною інтенсивністю надходить попит на 15 тис. одиниць товару, витрати на організацію постачання складають 10 дол. за одну партію, ціна одиниці товару - 3 дол.. а витрати на її збереження - 0,75 дол. у рік. Знайдіть оптимальний розмір партії.
2. Одноканальна система масового обслуговування (СМО) являє собою одну телефонну лінію. Заявка — виклик, що прийшла в момент зайнятої лінії, одержує відмовлення. Потік викликів надходить з інтенсивністю λ=1,1 (викликів за хвилину). Середня тривалість розмови tоб=2 хв. Усі потоки подій найпростіші. Потрібно визначити граничні значення:
1) відносної пропускної здатності q;
2) абсолютної пропускної здатності А;
3) ймовірності відмовлення Рвдм.
3. Система управління запасами описується моделлю виробничих постачань і має наступні значення параметрів. Попит дорівнює 1,5 тис. одиниць у рік, ціна 2 дол., витрати збереження одиниці товару протягом року - 0,2 дол., організаційні витрати -10 дол. Протягом року може бути зроблено 4,5 тис. одиниць товару при повному завантаженні виробничої лінії.
Список рекомендованої літератури
1. Бахтінова А.П., Гиль О.О., Гришина Л.О. Організація виробництва: практикум: навчальний посібник. – Львів: Новий світ, 2008. – 216 с.
2. Васильков В.Г. Організація виробництва: Навч. посібн. – К.: КНЕУ, 2003.
3. Організація виробництва. Навч. посібник. Під. ред. проф. Редькін О.В. – К.: Лібра, 2003.
4. Орлов О.О. Планування діяльності підприємства: Підручник. – К.: Скарби. – 2002. – 336 с.
5. Організація виробництва: Навч. посіб. для студ. вищ. навч. закл. / В.О. Онищенко, О.В. Редкін, А.С. Старовірець, В.Я. Черганова. – К.: Скарби, 2002. – 335 с.
6. Пащенко І.Н., Чернобай Л.І. Проектування організації виробництва промислового підприємства // Вісник ДУ Львівська політехніка – 2002 №448. – С. 95-100.
7. Пащенко І.Н., Чернобай Л.І. Основи методики проектування виробництва промислового підприємства // Вісник ДУ Львівська політехніка – 2000 №391. – С. 39-46.
8. Петрович Й.М., Захарчин Г.М., Буняк С.О. Організація виробництва: Практикум. – К.: Центр навчальної літератури, 2005. – 336 с.
9. Петрович Й.М., Захарчин Г.М. Організація виробництва: підручник. – Львів: Магнолія плюс, 2006. – 400 с.
10. Петрович Й.М., Захарчин Г.М., Теребух А.А. Організація підприємництва в Україні. Навчальний посібник. – Львів: Оксарт, 2000 – 320 с.
11. Плоткін Я.Д., Пащенко І.Н. Виробничий менеджмент. Навчальний посібник. – Львів: ДУ "ЛПІ", 1999. – 258 с.
12. Фатхутдинов Р.А. Организация производства: Учебник. – М.: ИНФРА-М, – 2000. – 672 с.
Додаток 1
Форма завдання
ІНДИВІДУАЛЬНЕ ЗАВДАННЯ
на виконання контрольної роботи студента ___________________________________________________
(прізвище, ім’я та по батькові)
1._____________________________________________________________________
2._____________________________________________________________________
3.________________________________________________________________________
Видано «___»_________________ 20_ р.
Прийнято «___»_________________ 20_ р.
Оцінка виконання завдання ____________________________________
Керівник
___________ ______________________
(підпис) (посада, прізвище, ініціали)
НАВЧАЛЬНЕ ВИДАННЯ
МЕТОДИЧНІ ВКАЗІВКИ
до виконання контрольної
з дисципліни «Прийняття управлінських рішень»
для студентів напряму підготовки 6.030601 «Менеджмент»
Укладачі: Мірошник Роман Олександрович
Редактор
Комп’ютерне складання
