Метод Гаусса с выбором главного элемента

Задания И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ «ЧИСЛЕННЫЕ МЕТОДЫ»

для студентов направления
27.03.04 «Управление в технических системах» (УПТС)

 

 

 

Саратов 2015

Цель работы

Ознакомление студентов с методами решения систем линейных алгебраических уравнений, получение навыков решения задач вычислительной математики на ЭВМ.

Задачи работы

Закрепление, углубление и расширение знаний студентов при решении практических вычислительных задач. Овладение вычислительными методами и практическими методами оценки погрешности вычислений. Приобретение умений и навыков при программировании и отладке вычислительных задач на компьютере.

Теоретическая часть

Прямые методы решения систем линейных алгебраических уравнений

Метод Гаусса

Одним из основных прямых методов решения СЛАУ является метод последовательного исключения неизвестных Гаусса. Он основан на возможности приведения исходной системы к эквивалентному представлению, когда относительно х решается задача с верхнетреугольной матрицей с единичной диагональю:

(1)

где , при j < i.

Получение этой системы, т.е. построение матрицы U и вектора у составляют, так называемый, прямой ход метода исключения Гаусса. Дальнейшее решение системы Ux = у — обратный ход метода исключения.

а) Прямой ход исключения. Опишем последовательно как он выполняется. шаг. Пусть . Тогда, деля первое уравнение на , получим

, .

Комбинируя полученное уравнение с остальными уравнениями системы (1), исключая в них переменную , найдем:

Для оставшихся уравнений (без ), повторим описанную процедуру: шаг. После (s — 1) шагов исключения часть переменных исключена

 

и мы получаем систему:

()

Положим . Делим s-oe уравнение на и находим

Используем полученное уравнение. После умножения его на , и вычитания из i-гo уравнения исключаем x_s в системе (*) из остальных уравнений.

Получим

=

=

= ,

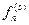где

= ;

= ;

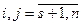
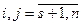
Таким образом прямой ход в методе Гаусса

осуществляется по формулам:

s = 1,..., n; j = s + 1,..., n

(4)

, j = s + 1,.., n; s = 1,..., n – 1

для матрицы и для правой части по формулам:

(5)

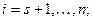
б) Обратный ход метода Гаусса. Теперь решаем систему Ux = у с верхне­треугольной матрицей, причём = 1:

 

(6)

 

Для реализации метода Гаусса требуется примерно (2/3)m³ арифметических операций, причем большинство из них приходится на прямой ход.

Ограничение метода единственного деления заключается в том, что угловые элементы не равны нулю, т.е. .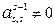

 

Метод Гаусса с выбором главного элемента

Может оказаться так, что система имеет единственное решение, хотя какой либо из миноров матрицы А равен нулю. Заранее неизвестно, что все угловые миноры матрицы А не равны нулю. Избежать этого можно с выбором главного элемента. Основная идея метода состоит в том, чтобынаочередном шаге исключать не следующее по номеру неизвестное, а то неизвестное, коэффициент при котором является наибольшим по модулю. Таким образом, в качестве ведущего элемента здесь выбирается главный, т. е. наибольший по модулю элемент.

Различные варианты метода Гаусса с выбором главного элемента проиллюстрируем на примере системы из двух уравнений.

 

1. Выбор главного элемента по строке

Пусть дана система второго порядка

(7)

при ½ а₁₂ ½>½ а₁₁ ½, тогда на первом шаге вместо неизвестного х₁ исключают х₂:

. (8)

К системе (8) применяем первый шаг прямого хода метода Гаусса. Указан­ный способ исключения называется методом Гаусса с выбором глав­ного элемента по строке. Он эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация переменных.

 

2. Выбор главного элемента по столбцу

Предположим, что ½ а₂₁ ½>½ а₁₁ ½и переставим уравнения системы (7)

(9)

и к системе (9) применяем первый шаг прямого хода метода Гаусса.

Таким образом, метод Гаусса с выбором главного элемента по столбцу эквивалентен применению обычного метода Гаусса к систе­ме, в которой на каждом шаге исключения проводится соответ­ствующая перенумерация уравнений.

 

3. Выбор главного элемента по всей матрице

Поиск главного элемента по всей матрице заключается в нахождении максимального по модулю элемента среди всех элементов матрицы системы. Всё это приводит к уменьшению вычислительной погрешности.