1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю.
По третьему закону динамики
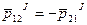
аналогичный результат для любой пары точки.
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси = 0.
Однако, не следует, что внутри силы взаимно уравновешиваются и не влияют на движение системы.
Эти силы приложены к разным точкам механической системы и могут вызывать взаимное перемещение точек системы.
Дифференциальные уравнения движения механической системы.
Система точек
.
обозначим массу каждой точки 
, и в каждую точку проведем 
, 
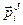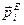равнодействие, приложенных к i-точке внутренних и внешних сил.
основное уравнение динамики
(i = 1… n)
спроектируем его на координатной оси.
(4.1) дифференциальные уравнения движения
механической системы
Проинтегрировать эти уравнения удается лишь в исключительных случаях. Основная их роль состоит в том, что они или следствия из них, являются исходными для получения общих теорем динамики.
Центр масс механической системы и его координаты. Твердое тело.
Каждая точка 
имеет определенную массу и положение относительно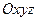 
определяется или 
.
Центром масс называется геометрическая точка с, радиус-вектор который
где 
масса всей системы.
Проектируя (4.2) на координатной оси.
(4.3)
Вывод. Центр масс является не материальной точкой, а геометрически он может не совпадать ни с одной из материальных точек системы (кольцо).
Центр масс характеризует распределение масс в системе.
Из формул (4.3), (4.2) видно, что положение центра масс системы зависит только от положения и массы каждой точки этой системы.
Центр тяжести тел является центром масс этой системы.
(Статика) 
Понятие «центр масс» применимо для любой системы материальной точки, тогда как понятие «центр тяжести» применяется лишь для механических систем, находящихся в однородном поле силы тяжести.
Твердое тело.
Рассмотрим систему точек, расстояние между которыми не меняется. Такая система называется неизменяемой.
|
|
 |
Для образования неизменной системы каждую точку нужно соединить идеальными стержнями по крайней мере с тремя точками, уже входящими в неизменную систему.
Считая число точек неизменяемой системы бесконечно большим, а длины соединяющих их идеальных стержней бесконечно малыми, получаем модель абсолютно твердого тела.
Теорема о движении центра масс.
()
Уравнения движения этих точек
(i = 1, 2 … n)
Суммируем эти уравнения.
Преобразуем левую часть равенства
т.к. Получаем:
или
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил или главному вектору этих сил.
Уравнение выражает теорему о движении центра масс системы, которая формируется следующим образом: центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему.
Проектируя (4.5) на координатные оси
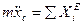Это дифференциальные уравнения движения центра
масс системы
Следствия из теоремы
1. Если 
, то центр масс механической системы находится в покое, или движется равномерно и прямолинейно.
, 
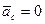, т.е. 
.
2. Если 
проекций внешних сил на какую-либо ось равна нулю, то проекция центра масс механической системы на эту ось или неподвижна или движется равномерно.
Пусть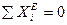 
, тогда 
, т.е. 
, если при этом в начальный момент , то 
.
