Между различного рода признаками, случайными величинами практически всегда существует взаимосвязь. Только иногда эту связь мы замечаем, но в большинстве случаев эти взаимосвязи ускользают от нашего внимания.
В одних случаях получается функциональная связь, когда между признаками  и
и  существует однозначная зависимость:
существует однозначная зависимость:  . Например
. Например  ,
,  и т.д.
и т.д.
В других случаях получается корреляционная зависимость, когда одному значению признака  соответствуют несколько значений признака
соответствуют несколько значений признака  . То есть здесь мы имеем дело со статистической связью. Например, связь между ростом человека и его весом, связь между стажем работника и качеством его труда и т.д.
. То есть здесь мы имеем дело со статистической связью. Например, связь между ростом человека и его весом, связь между стажем работника и качеством его труда и т.д.
Корреляционная связь между признаками может быть линейной и нелинейной, положительной и отрицательной. Задача корреляционного анализа сводится к установлению формы и направления связи между признаками, измерению ее тесноты и к оценке достоверности выборочных коэффициентов корреляции.
Корреляционным моментом  случайных величин
случайных величин  и
и  называют математическое ожидание произведения отклонений этих величин от своих математических ожиданий:
называют математическое ожидание произведения отклонений этих величин от своих математических ожиданий:

Корреляционный момент служит для характеристики связи между величинами  и
и  .
.
Корреляционный момент равен нулю, если  и
и  независимы, следовательно, если корреляционный момент не равен нулю, то
независимы, следовательно, если корреляционный момент не равен нулю, то  и
и  — в какой-то степени зависимые случайные величины.
— в какой-то степени зависимые случайные величины.
Теорема 1. Корреляционный момент двух независимых случайных величин  и
и  равен нулю.
равен нулю.
Доказательство: т.к.  и
и  — независимые случайные величины, то их отклонения от своих математических ожиданий
— независимые случайные величины, то их отклонения от своих математических ожиданий  и
и  также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим
также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим
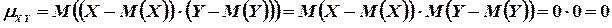
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин  и
и  , т.е. величина корреляционного момента зависит от единиц измерения случайных величин. Поэтому для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины.
, т.е. величина корреляционного момента зависит от единиц измерения случайных величин. Поэтому для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины.
Такая особенность корреляционного момента является недостатком этой числовой характеристики, т.к. сравнение корреляционных моментов различных систем случайных величин становится затруднительным. Для того чтобы устранить этот недостаток, вводят новую числовую характеристику—коэффициент корреляции  .
.
Коэффициентом корреляции случайных величин  и
и  называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

Так как размерность  равна произведению размерностей величин
равна произведению размерностей величин  и
и  ,
,  имеет размерность величины
имеет размерность величины  ,
,  имеет размерность величины
имеет размерность величины  , то
, то  — безразмерная величина.
— безразмерная величина.
Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом и состоит преимущество коэффициента корреляции перед корреляционным моментом.
Очевидно, коэффициент корреляции независимых случайных величин равен нулю (т.к.  ).
).
Абсолютная величина коэффициента корреляции не превышает единицы: 
На практике мы имеем дело с выборками, а не с генеральными совокупностями. Поэтому на практике рассчитывают выборочный коэффициент корреляции, который может быть достоверным или нет. Выборочный коэффициент корреляции рассчитывается по следующей формуле:
 (5.10)
(5.10)
Коэффициент корреляции удобный показатель связи, получивший широкое применение в практике. Это отвлеченное число, лежащее в пределах от -1 до +1. При независимом варьировании признаков, когда связь между ними отсутствует,  . При
. При  существует положительная связь между признаками (с ростом
существует положительная связь между признаками (с ростом  растет и
растет и  ). При
). При  - отрицательная связь - с ростом признака
- отрицательная связь - с ростом признака  признак
признак  уменьшается. Чем больше
уменьшается. Чем больше  по модулю, тем теснее связь между признаками. При
по модулю, тем теснее связь между признаками. При 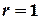 между признаками существует функциональная связь.
между признаками существует функциональная связь.
Лишь один недостаток имеется у этого ценного показателя - он способен характеризовать лишь линейный связи. При наличии нелинейной связи между коррелирующими признаками следует использовать другие показатели.
Выборочный коэффициент корреляции служит оценкой генерального параметра  , и, как случайная величина, сопровождается ошибками. Поэтому здесь также проверяется гипотеза о значимости выборочного коэффициента корреляции.
, и, как случайная величина, сопровождается ошибками. Поэтому здесь также проверяется гипотеза о значимости выборочного коэффициента корреляции.
Пусть двумерная генеральная совокупность  распределена нормально. Из этой совокупности извлечены выборки объемом
распределена нормально. Из этой совокупности извлечены выборки объемом  и по ним найден выборочный коэффициент корреляции
и по ним найден выборочный коэффициент корреляции  , который оказался отличным от нуля. Так как выборки отобраны случайно, еще нельзя заключить, что коэффициент корреляции генеральной совокупности
, который оказался отличным от нуля. Так как выборки отобраны случайно, еще нельзя заключить, что коэффициент корреляции генеральной совокупности  также отличен от нуля. А, поскольку нас интересует именно этот коэффициент, возникает необходимость при заданном уровне значимости
также отличен от нуля. А, поскольку нас интересует именно этот коэффициент, возникает необходимость при заданном уровне значимости  проверить нулевую гипотезу
проверить нулевую гипотезу  :
:  о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе
о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе  :
:  .
.
Если нулевая гипотеза отвергается, значит, выборочный коэффициент корреляции значимо отличается от нуля (кратко говоря, значим), а  и
и  коррелированны, т. е. связаны линейной зависимостью.
коррелированны, т. е. связаны линейной зависимостью.
Если же нулевая гипотеза будет принята, значит, выборочный коэффициент корреляции является незначимым, а  и
и  некоррелированные, т. е. не связаны линейной зависимостью.
некоррелированные, т. е. не связаны линейной зависимостью.
В качестве критерия проверки нулевой гипотезы примем случайную величину

Величина  при справедливости нулевой гипотезы имеет распределение Стьюдента с
при справедливости нулевой гипотезы имеет распределение Стьюдента с  степенями свободы.
степенями свободы.
Обозначим значение критерия, вычисленное по данным наблюдений, через  и сформулируем правило проверки нулевой гипотезы.
и сформулируем правило проверки нулевой гипотезы.
Правило. Для того чтобы при заданном уровне значимости 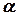 проверить нулевую гипотезу
проверить нулевую гипотезу  :
: 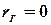 о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе
о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе  :
:  , надо вычислить наблюдаемое значение критерия:
, надо вычислить наблюдаемое значение критерия:
 (5.11)
(5.11)
и по таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы  найти критическую точку
найти критическую точку  .
.
Если 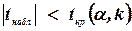 — нет оснований отвергнуть нулевую гипотезу, если
— нет оснований отвергнуть нулевую гипотезу, если  - то ее отвергают.
- то ее отвергают.
В то время как задача корреляционного анализа - установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа - описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии 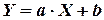 , где
, где
 ,
,  (5.12)
(5.12)
Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение  известно, а
известно, а  - нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для
- нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для  и
и  видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
7. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.
Ранее предполагалось, что закон распределения генеральной совокупности известен. Если же он неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его  ), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону
), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону  .
.
Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т. е. при помощи специально подобранной случайной величины — критерия согласия.
Критерием согласия  называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Имеется несколько критериев согласия, но мы ограничимся описанием применения критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для др. распределений). Для этого будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.
Обычно эмпирические и теоретические частоты различаются. Возможно, что расхождение случайно (незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.
Критерий Пирсона отвечает на вопрос «Случайно ли расхождение частот?». Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.
Итак, пусть по выборке объема  получено эмпирическое распределение: варианты -
получено эмпирическое распределение: варианты -  :
:  , эмпирические частоты -
, эмпирические частоты -  :
: 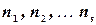 .
.
Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты  . При уровне значимости
. При уровне значимости 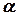 требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.
требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.
В качестве критерия проверки нулевой гипотезы примем случайную величину
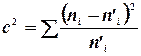 .
.
Эта величина случайная, т.к. в различных опытах она принимает различные, заранее не известные значения. Ясно, что, чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.
Стоит заметить, что возведение в квадрат разностей частот устраняет возможность взаимного погашения положительных и отрицательных разностей. Делением на  достигают уменьшения каждого из слагаемых – иначе сумма была бы настолько велика, что приводила бы к отклонению нулевой гипотезы даже тогда, когда она справедлива.
достигают уменьшения каждого из слагаемых – иначе сумма была бы настолько велика, что приводила бы к отклонению нулевой гипотезы даже тогда, когда она справедлива.
Доказано, что при  закон распределения случайной величины
закон распределения случайной величины  независимо от того, к какому закону распределения подчинена генеральная совокупность, стремится к закону распределения
независимо от того, к какому закону распределения подчинена генеральная совокупность, стремится к закону распределения  с
с 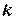 степенями свободы. Поэтому случайная величина
степенями свободы. Поэтому случайная величина  обозначена через
обозначена через  , а сам критерий называют критерием согласия «хи квадрат».
, а сам критерий называют критерием согласия «хи квадрат».
Число степеней свободы находят по равенству  , где
, где  — число групп выборки;
— число групп выборки;  — число параметров предполагаемого распределения, которые оценены по данным выборки.
— число параметров предполагаемого распределения, которые оценены по данным выборки.
В частности, если предполагаемое распределение — нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому  и число степеней свободы
и число степеней свободы  .
.
Так как односторонний критерий более жестко отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 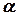 :
:
 .
.
Обозначим значение критерия, вычисленное по данным наблюдений, через  и сформулируем правило проверки нулевой гипотезы.
и сформулируем правило проверки нулевой гипотезы.
Правило: для того чтобы при заданном уровне значимости проверить нулевую гипотезу  (генеральная совокупность распределена нормально), надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
(генеральная совокупность распределена нормально), надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
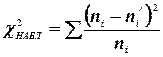
и по таблице критических точек распределения  , по заданному уровню значимости
, по заданному уровню значимости 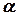 и числу степеней свободы
и числу степеней свободы  найти критическую точку
найти критическую точку  . Если
. Если  — нет оснований отвергнуть нулевую гипотезу, если
— нет оснований отвергнуть нулевую гипотезу, если  — нулевую гипотезу отвергают.
— нулевую гипотезу отвергают.






