ПРИМЕНЕНИЕ ТЕОРИИ ВЕРОЯТНОСТИ К СТАТИСТИКЕ.
Оглавление.
1. Основные понятия.
2. Определение неизвестной функции распределения.
3. Определение неизвестных параметров распределения.
4. Доверительный интервал. Доверительная вероятность.
5. Применение критерия Стьюдента для сравнения генеральных
совокупностей.
6. Элементы теории корреляции.
7. Проверка гипотезы о нормальном распределении генеральной
совокупности. Критерий согласия Пирсона.
Основные понятия.
Математическая статистика - это раздел математики, в котором изучаются методы обработки и анализа экспериментальных данных, полученных в результате наблюдений над массовыми случайными событиями, явлениями.
Наблюдения, проводимые над объектами, могут охватывать всех членов изучаемой совокупности без исключения и могут ограничиваться обследованиями лишь некоторой части членов данной совокупности. Первое наблюдение называется сплошным или полным, второе частичным или выборочным.
Естественно, что наиболее полную информацию дает сплошное наблюдение, однако к нему прибегают далеко не всегда. Во-первых, сплошное наблюдение очень трудоемко, а во-вторых, часто бывает практически невозможно или даже нецелесообразно. Поэтому в подавляющем большинстве случаев прибегают к выборочному исследованию.
Совокупность, из которой некоторым образом отбирается часть ее членов для совместного изучения, называется генеральной совокупностью, а отобранная тем или иным способом часть генеральной совокупности - выборочная совокупность или выборка.
Объем генеральной совокупности  теоретически ничем неограничен
теоретически ничем неограничен  , на практике же он всегда ограничен.
, на практике же он всегда ограничен.
Объем выборки  может быть большим или малым, но он не может быть меньше двух.
может быть большим или малым, но он не может быть меньше двух.
Отбор в выборку можно проводить случайным способом (по способу жеребьевки или лотереи). Либо планово, в зависимости от задачи и организации обследования. Для того, чтобы выборка была представительной, необходимо обращать внимание на размах варьирования признака и согласовывать с ним объем выборки.
2. Определение неизвестной функции распределения.
Итак, мы сделали выборку. Разобьем диапазон наблюдаемых значений  на интервалы
на интервалы  ,
,  , ….
, ….  одинаковой длины
одинаковой длины  . Для оценки необходимого числа интервалов
. Для оценки необходимого числа интервалов 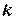 можно использовать следующие формулы:
можно использовать следующие формулы:
 . (5.1)
. (5.1)
Далее пусть mi - число наблюдаемых значений  , попавших в i -ый интервал. Разделив mi на общее число наблюдений n, получим частоту
, попавших в i -ый интервал. Разделив mi на общее число наблюдений n, получим частоту  , соответствующую i -ому интервалу:
, соответствующую i -ому интервалу:  , причем
, причем  . Составим следующую таблицу:
. Составим следующую таблицу:
| Номер интервала | Интервал | mi | 
|

| m1 | 
| |

| m2 | 
| |
| ... | ... | ... | ... |
| k | 
| mk | 
|
которая называется статистическим рядом. Эмпирической (или статистической) функцией распределения случайной величины  называется частота события, заключающегося в том, что величина
называется частота события, заключающегося в том, что величина  в результате опыта примет значение, меньшее x:
в результате опыта примет значение, меньшее x:

На практике достаточно найти значения статистической функции распределения F*(x) в точках  , которые являются границами интервалов статистического ряда:
, которые являются границами интервалов статистического ряда:
 (5.2)
(5.2)
Следует заметить, что  при
при 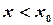 и
и  при
при  . Построив точки
. Построив точки  и соединив их плавной кривой, получим приближенный график эмпирической функции распределения (рис. 5.1). Используя закон больших чисел Бернулли, можно доказать, что при достаточно большом числе испытаний
и соединив их плавной кривой, получим приближенный график эмпирической функции распределения (рис. 5.1). Используя закон больших чисел Бернулли, можно доказать, что при достаточно большом числе испытаний  с вероятностью, близкой к единице, эмпирическая функция распределения
с вероятностью, близкой к единице, эмпирическая функция распределения  отличается сколь угодно мало от неизвестной нам функции распределения
отличается сколь угодно мало от неизвестной нам функции распределения  случайной величины
случайной величины  .
.

Часто вместо построения графика эмпирической функции распределения поступают следующим образом. На оси абсцисс откладывают интервалы  ,
,  ,….
,….  . На каждом интервале строят прямоугольник, площадь которого равна частоте
. На каждом интервале строят прямоугольник, площадь которого равна частоте  , соответствующей данному интервалу. Высота hi этого прямоугольника равна
, соответствующей данному интервалу. Высота hi этого прямоугольника равна  , где
, где  - длинна каждого из интервалов. Ясно, что сумма площадей всех построенных прямоугольников равна единице.
- длинна каждого из интервалов. Ясно, что сумма площадей всех построенных прямоугольников равна единице.
Рассмотрим функцию  , которая в интервале
, которая в интервале  постоянна и равна
постоянна и равна  . График этой функции называется гистограммой. Он представляет собой ступенчатую линию (рис. 5.2). С помощью закона больших чисел Бернулли можно доказать, что при малых
. График этой функции называется гистограммой. Он представляет собой ступенчатую линию (рис. 5.2). С помощью закона больших чисел Бернулли можно доказать, что при малых  и больших
и больших  с практической достоверностью
с практической достоверностью  как угодно мало отличается от плотности распределения
как угодно мало отличается от плотности распределения  непрерывной случайной величины
непрерывной случайной величины  .
.
Таким образом на практике определяется вид неизвестной функции распределения случайной величины.
3. Определение неизвестных параметров распределения.
Таким образом мы получили гистограмму, которая дает наглядность. Наглядность представленных результатов позволяет сделать различные заключения, суждения об исследуемом объекте.
Однако на этом обычно не останавливаются, а идут дальше, анализируя данные на проверку определенных предположений относительно возможных механизмов изучаемых процессов или явлений.
Несмотря на то, что данных в каждом обследовании сравнительно немного, мы бы хотели, чтобы результаты анализа достаточно хорошо описывали бы все реально существующее или мыслимое множество (т.е. генеральную совокупность).
Для этого делают некоторые предположения о том, как вычисленные на основе экспериментальных данных (выборке) показатели соотносятся с параметрами генеральной совокупности.
Решение этой задачи составляет главную часть любого анализа экспериментальных данных и тесно связано с использованием ряда теоретических распределений, рассмотренных выше.
Широкое использование в статистических выводах нормального распределения имеет под собой как эмпирическое, так и теоретическое обоснование.
Во-первых, практика показывает, что во многих случаях нормальное распределение действительно является довольно точным представлением экспериментальных данных.
Во-вторых, теоретически показано, что средние значения интервалов гистограмм распределены по закону, близкому к нормальному.
Однако следует четко представлять, что нормальное распределение - это лишь чисто математический инструмент и совсем необязательно, чтобы реальные экспериментальные данные точно описывались нормальным распределением. Хотя во многих случаях, допуская небольшую ошибку, можно говорить, что данные распределены нормально.
Ряд показателей, такие как среднее, дисперсия и т.д., характеризуют выборку и называются статистиками. Такие же показатели, но относящиеся к генеральной совокупности в целом, называются параметрами. Таким образом, можно сказать, что статистики служат для оценки параметров.
Генеральной средней  называется среднее арифметическое значений
называется среднее арифметическое значений  генеральной совокупности объема
генеральной совокупности объема  :
:

Выборочной средней  называется среднее арифметическое выборки
называется среднее арифметическое выборки  объема
объема  :
:
 , (5.3)
, (5.3)
или
 (5.4)
(5.4)
если выборка имеет вид таблицы.
Выборочную среднюю принимают в качестве оценки генеральной средней.
Генеральной дисперсией  называется среднее арифметическое квадратов отклонения значений генеральной совокупности
называется среднее арифметическое квадратов отклонения значений генеральной совокупности  от их среднего значения
от их среднего значения  :
:

Генеральным средним квадратическим отклонением  называется корень квадратный из генеральной дисперсии:
называется корень квадратный из генеральной дисперсии:  .
.
Выборочной дисперсией  называется среднее арифметическое квадратов отклонения значений выборки
называется среднее арифметическое квадратов отклонения значений выборки  от их среднего значения
от их среднего значения  :
:

Выборочное среднее квадратическое отклонение  определяется как
определяется как  .
.
Для лучшего совпадения с результатами экспериментов, вводят понятие эмпирической (или исправленной) дисперсии  :
:

Для оценки генерального среднего квадратического отклонения служит исправленное среднее квадратическое отклонение, или эмпирический стандарт  :
:
 (5.5)
(5.5)
В случае, когда все значения выборки  различны, т.е.
различны, т.е.  ,
,  , формулы для
, формулы для  и
и  принимают вид:
принимают вид:
 (5.6)
(5.6)
Доверительный интервал. Доверительная вероятность.
Различные статистики, получаемые результате вычислений, представляют собой точечные оценки соответствующих параметров генеральной совокупности.
Если из генеральной совокупности извлечь некоторое количество выборок и для каждой из них найти интересующие нас статистики, то вычисленные значения будут представлять собой случайные величины, имеющие некоторый разброс вокруг оцениваемого параметра.
Но, как правило, в результате эксперимента в распоряжении исследователя имеется одна выборка. Поэтому значительный интерес представляет получение интервальной оценки, т.е. некоторого интервала, внутри которого, как можно предположить, лежит истинное значение параметра.
Вероятности, признанные достаточными для уверенных суждениях о параметрах генеральной совокупности на основании статистик, называются доверительными.
Для примера рассмотрим  как оценку параметра
как оценку параметра  .
.
Известно, что если выборки извлекаются из генеральной совокупности с параметрами:

то распределение выборочных средних  будет иметь среднее, равное
будет иметь среднее, равное  , дисперсию
, дисперсию  , среднее квадратическое
, среднее квадратическое  , где
, где  - объем выборки и будет приближаться к нормальному.
- объем выборки и будет приближаться к нормальному.
Для такого распределения, как известно,  наблюдений лежит в интервале
наблюдений лежит в интервале  ,
, 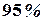 в интервале
в интервале  и
и  в интервале
в интервале  .
.
 (5.7)
(5.7)
где  .
.
С надежностью  доверительный интервал
доверительный интервал  покрывает неизвестный параметр
покрывает неизвестный параметр  с точностью
с точностью  . Здесь мы задаемся надежностью
. Здесь мы задаемся надежностью  , а зная
, а зная  по таблицам для функции Лапласа находим параметр
по таблицам для функции Лапласа находим параметр  и далее - доверительный интервал.
и далее - доверительный интервал.
Но истинное значение параметра генеральной совокупности  нам неизвестно. Поэтому на практике вместо параметра
нам неизвестно. Поэтому на практике вместо параметра  используют выборочное среднее квадратическое отклонение
используют выборочное среднее квадратическое отклонение  . То есть доверительный интервал определяется выражением
. То есть доверительный интервал определяется выражением
 (5.8)
(5.8)
Но здесь параметр  уже параметр распределения Стьюдента, который находится по соответствующим таблицам при данных
уже параметр распределения Стьюдента, который находится по соответствующим таблицам при данных  и
и  , где
, где  - задаваемая надежность. Этот интервал покрывает неизвестный параметр
- задаваемая надежность. Этот интервал покрывает неизвестный параметр  с надежностью
с надежностью  , где
, где  и
и  находятся по формулам (5,3), (5.4) и (5.5), (5.6) соответственно.
находятся по формулам (5,3), (5.4) и (5.5), (5.6) соответственно.
Пример. Найти доверительный интервал для оценки математического ожидания  нормальной случайной величины с надежностью
нормальной случайной величины с надежностью  , зная выборочную среднюю
, зная выборочную среднюю 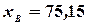 , объем выборки
, объем выборки  , среднее квадратическое отклонение
, среднее квадратическое отклонение  .
.
Решение. Имеем  . Отсюда
. Отсюда 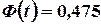 . По таблице значений функции Лапласа находим
. По таблице значений функции Лапласа находим  . Отсюда
. Отсюда







