ПОСЛЕДОВАТЕЛЬНЫЕ ИСПЫТАНИЯ.
Оглавление.
1. Вероятность появления хотя бы одного события.
2. Формула Бернулли.
3. Приближения формулы Бернулли.
Вероятность появления хотя бы одного события.
Пусть в результате испытания могут появиться п событий, независимых в совокупности, либо некоторые из них (в, частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Чтобы найти вероятность того, что наступит хотя бы одно из этих событий, воспользуемся следующей теоремой.
Теорема 4: вероятность появления хотя бы одного из событий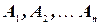 
, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 
:
.
Доказательство: обозначим через А событие, состоящее в появлении хотя бы одного из событий 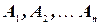. События А и (ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице:
.
Отсюда, пользуясь теоремой умножения, получим
,
или
. (2.1)
Частный случай: если события 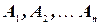имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий равна
. (2.2)
Формула Бернулли
Предположим теперь, что производится n независимых испытаний в неизменных условиях, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А одинакова и равна 
. Следовательно, вероятность противоположного события (ненаступления А) равна 
.
Определим вероятность 
того, что событие А произойдет m раз при этих n испытаниях.
При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв 
и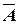 
. Например, запись 
означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.
Всякую комбинацию, в которую входит 
раз и, соответственно, 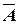входит 
раз, назовем благоприятной. Количество благоприятных комбинаций равно количеству 
способов, которыми можно выбрать чисел из данных 
; таким образом, оно равно числу сочетаний из n элементов по m, т.е.
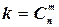
Подсчитаем теперь вероятности благоприятных комбинаций. Рассмотрим сначала случай, когда событие A происходит в первых испытаниях и, следовательно, не происходит в остальных испытаниях. Такая благоприятная комбинация имеет следующий вид:
Вероятность этой комбинации в силу независимости испытаний (на основании теоремы умножения вероятностей) составляет
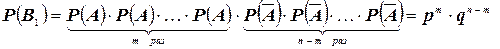
Так как в любой другой благоприятной комбинации 
событие встречается также раз, а событие 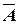происходит раз, то вероятность каждой из таких комбинаций также равна 
. Итак
Все благоприятные комбинации являются, очевидно, несовместными. Поэтому (на основании аксиомы сложения вероятностей)
Следовательно,
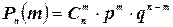(2.3)
Или, так как 
, то
(2.4)
Формула (2.4) называется формулой Бернулли (Я. Бернулли (1654-1705) - швейцарский математик).
Так как вероятности для различных значений представляют собой слагаемые в разложении бинома Ньютона:
то распределение вероятностей , где 
, называется биноминальным.
Пример 9. Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 8 выстрелов дадут 5 попаданий?
Решение: Здесь n = 8; m = 5; p = 0,6; q = 1- 0,6 = 0,4.
Используя формулу (2.4), имеем
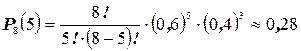
Часто необходимо знать, при каком значении 
вероятность принимает наибольшее значение, т. е. требуется найти наивероятнейшее число 
наступления события A в данной серии опытов. Можно доказать, что число 
должно удовлетворять двойному неравенству
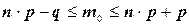(2.5)
Заметим, что сегмент 
, в котором лежит , имеет длину 
. Поэтому, если какой-либо из его концов не является целым числом, то между этими концами лежит единственное целое число, и определено однозначно. В том случае, если оба конца — целые числа, имеются два наивероятнейших значения: 
и 
.
Пример 10. Определить наивероятнейшее число попаданий в цель в примере 1.
Решение: Здесь 
; 
; 
; 
; 
.
Согласно формуле (2.5) наивероятнейшее значение лежит на сегменте 
и, следовательно, равно 5.
Приближения формулы Бернулли
При больших значениях n подсчет вероятностей по формуле (2.4) связан с громоздкими вычислениями. В этом случае удобнее пользоваться приближенными формулами.
1. Локальная формула Муавра-Лапласа.
(2.6)
где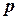 
не равно нулю и единице, 
, а
. (2.7)
Формула (2.6) выражает так называемую локальную теорему Лапласа (П. Лаплас (1749—1827) — французский математик и астроном.). Точность этой формулы повышается с возрастанием n.
Функция 
формула (2.7), как мы увидим в дальнейшем, играет очень большую роль в теории вероятностей (см. рис. 2.1). Ее значения при различных значениях аргумента приведены в Приложении (см. табл. I). Она представляет собой функцию вероятности нормального распределения (мы еще вернемся к ней). При 
, 
, поэтому функция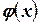 
затабулирована для 
.
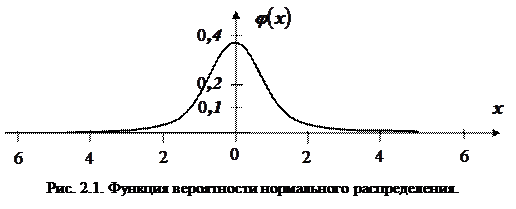
Пример 11. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз.
Решение: Здесь m=20; n=80; p=1/6; q=1-1/6=5/6; далее находим
Используя формулу (15), получим
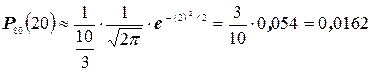
так как из табл. I находим, что 
.
2. Если 
то используют так называемую формулу Пуассона
(2.8)
Пример 12. Завод отправил 5000 доброкачественных изделий. Вероятность того, что в пути разбили одно изделие - 0,0002. Найти вероятность того, что в пути будет повреждено:
а) 3 изделия;
б) 1 изделие;
в) не более трех изделий.
Решение. Имеем 
и 
, поэтому применяем формулу Пуассона.
а) 
: 
.
б) 
: 
.
в) 
:
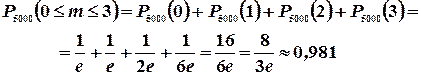
3. При больших значениях , для вычисления вероятности того, что произойдет от 
до 
событий по схеме Бернулли, используется интегральная формула Муавра-Лапласа:
где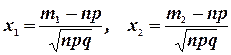 
,
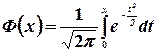(2.9)
- функция Лапласа (см. рис. 2.2.).
К функции Лапласа мы еще не раз будем обращаться, а пока отметим, что 
имеет следующие свойства.
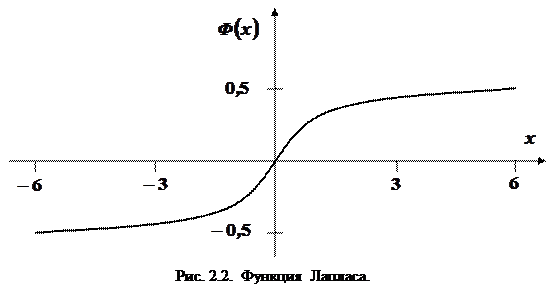
1) 
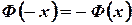- функция нечетная, поэтому достаточно применять ее для неотрицательных значений 
;
2) функция возрастает на всей числовой оси;
3) при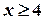 
, 
(
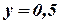- горизонтальная асимптота при 
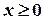), поэтому функция представлена в виде таблицы для 
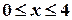(Прил. I);
4) вероятность отклонения относительной частоты 
от постоянной вероятности 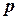в независимых испытаниях не более чем на некоторое число 
равна:
Пример 13. Стрелок выполнил 
выстрелов, вероятность одного попадания 
. Найти вероятность того, что он попадет от 
до 
раз.
Решение. Согласно интегральной формуле
, где
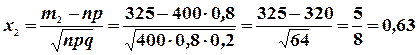
Пример 14. В каждом из 
независимых испытаний вероятность успеха 
. Найти вероятность того, что относительная частота появления события отклонится от постоянной вероятности по абсолютной величине не более чем на 
.
Решение. 
, следовательно
Пример 15. Сколько раз нужно бросить монету, чтобы с вероятностью 
можно было ожидать, что отклонение относительной частоты появления герба от вероятности 
окажется по абсолютной величине не больше чем на 
?
Решение. По условию 
. Отсюда
.
