Гомельский государственный
Технический университет им. П.О. Сухого
Кафедра ''Гидропневмоавтоматика''
Контрольные работы
По курсу
«Механика жидкости и газа»
для студентов специальности
1-36 01 07
«Гидропневмосистемы мобильных
и технологических машин»
заочной формы обучения
Гомель 2009
ЗАДАНИЕ 1.
Найти давление воздуха в резервуаре В, если избыточное давление на поверхности воды в резервуаре А равно Рa = 40∙103 н/м2. Уровни жидкостей в резервуаре А и двухколенном дифференциальном манометре расположились на высотах h, h1, h2, h3, h4. Пространство между уровнями ртути в манометре заполнено спиртом.
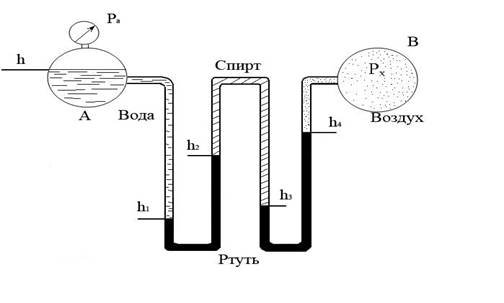
Плотность спирта ρс=0,8∙103 кг/м3, плотность ртути ρр=13∙103 кг/м3, h=1 м, h1=0,2 м
| Вариант | ||||||||||||
| h2, м | 0, 4 | 0, 4 | 0, 4 | 0,5 | 0,5 | 0,5 | 0,6 | 0,6 | 0,6 | 0,7 | 0,7 | 0,7 |
| h3, м | 0,1 | 0,2 | 0,1 | 0,2 | 0,1 | 0,2 | 0,1 | 0,2 | 0,1 | 0,2 | 0,1 | 0,2 |
| h4, м | 0, 4 | 0, 4 | 0,5 | 0,6 | 0,6 | 0,6 | 0,7 | 0,7 | 0,8 | 0,8 | 0,9 | 0,9 |
ЗАДАНИЕ 2.
Двухжидкостный микроманометр состоит из U -образной трубки диаметром d, соединяющей чашки диаметром D. Прибор заполнен несмешивающимися жидкостями с плотностями ρ1= 870 кг/м3, ρ2=830 кг/м3. Прибор измеряет разность давлений ∆P=P1-P2 по смещению мениска раздела жидкостей h от его начального положения, отвечающего ∆Р=0.
1.Определить ∆Р при заданном значении h.
2.Указать, во сколько раз уменьшатся показания прибора при данном ∆Р, если в приборе будут отсутствовать чашки.
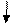
| Вариант | ||||||||||||
| D, мм | ||||||||||||
| d, мм | ||||||||||||
| h, см |
ЗАДАНИЕ 3.
Определить вес толстостенного колокола размерами D,d и L, если он плавает в воде при погружении Н. Перед погружением давление воздуха было равно атмосферному: 98,1∙103 н/м2
| Вариант | ||||||||||||
| D, мм | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 |
| d, мм | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 |
| L, м | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 |
| H, м | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 |
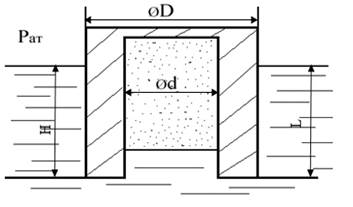
Процесс сжатия воздуха при погружении считать изотермическим: PV=P0V0.
ЗАДАНИЕ 4.
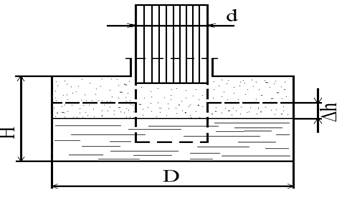
Цилиндрический сосуд диаметром D= 1 м и высотой Н=2,4 м заполнен водой до середины высоты, а давление воздуха в нем равно атмосферному: 98,1∙103 н/м2. Как изменится положение уровня воды в сосуде и давление воздуха в нем после опускания в сосуд плунжера, диаметр которого d, а масса m? Процесс сжатия воздуха, замкнутого в сосуде считать изотермическим:PV=P0V0.
Трением плунжера в герметической направляющей втулке пренебречь.
| Вариант | ||||||||||||
| d, мм | ||||||||||||
| m, кг |
ЗАДАНИЕ 5.
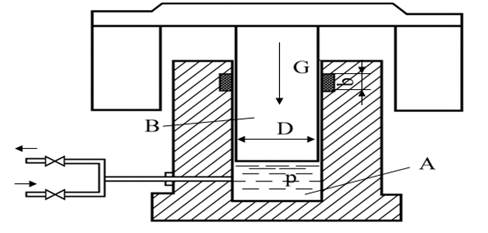
При зарядке гидравлического аккумулятора насос подает воду в цилиндр А, поднимая плунжер В вместе с грузом вверх. При разрядке аккумулятора плунжер, скользя вниз, выдавливает своим весом воду из цилиндра в гидравлические прессы. Определить:
Давление воды при зарядке (развиваемое насосом) и при разрядке (получаемое прессами) аккумулятора, если вес плунжера вместе с грузом G, а диаметр плунжера D.
2.Работу, затраченную на зарядку аккумулятора и работу, совершаемую аккумулятором при разрядке, если полная высота подъема плунжера Н=2 м.
3.Коэффициент полезного действия аккумулятора. Плунжер уплотнен манжетой, высота которой b = 60 мм, а коэффициент трения о плунжер f=0,1. Давление p воды в цилиндре аккумулятора считать одинаковым во всех точках. Силу трения T манжеты о плунжер под считать как произведение прижимающей силы на коэффициент трения: T=pπDbf
| Вариант | ||||||||||||
| G, кН | ||||||||||||
| D, м | 0,3 | 0,3 | 0,4 | 0,4 | 0,5 | 0,5 | 0,6 | 0,6 | 0,7 | 0,7 | 0,8 | 0,9 |
ЗАДАНИЕ 6.
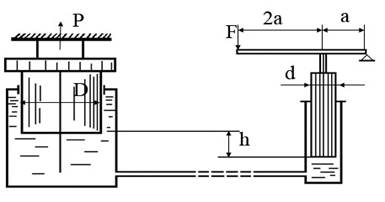
Вычислить силу опрессовки детали P при заданном усилии F на конце рычага. Известны: масса малого поршня m=0,3 кг, масса большого – М = 8 кг; a= 0,2 м; D=5∙d; h=0,5 м. Плотность рабочей жидкости ρ=900 кг/м3.
| Вариант | ||||||||||||
| Р, н | ||||||||||||
| d, мм |
ЗАДАНИЕ 7.
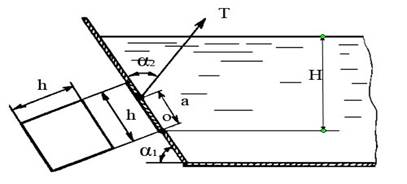
Определить необходимое натяжение каната Т и силу реакции R0 на оси поворота 0 щита, закрывающего квадратное отверстие в плоской стенке. В резервуаре находится вода. α1 = 50°, α2 = 60°.
| Вариант | ||||||||||||
| H, м | ||||||||||||
| h, м | ||||||||||||
| a, м | 1,4 | 1,6 | 2,4 | 2,5 | 3,5 |
ЗАДАНИЕ 8.
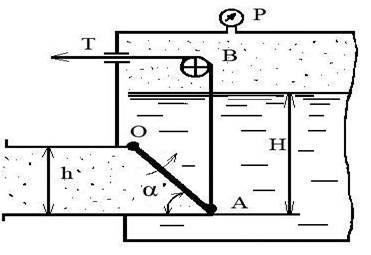
Поворотный клапан АО закрывает выход из бензохранилища в трубу квадратного сечения со стороной h=0,35 м. Прямоугольная пластина клапана опирается на срез трубы, сделанный под углом α=45°. В трубе жидкость отсутствует. Определить (без учета трения в опоре 0 клапана и в ролике В) силу Т натяжения троса, необходимую для открытия клапана, если уровень бензина Н, а давление над ним по манометру избыточное) Р. Плотность бензина ρ = 700 кг/м3.
| Вариант | ||||||||||||
| H, м | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 |
| Р, кПа |
ЗАДАНИЕ 9.
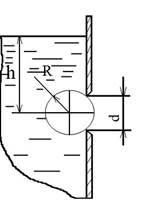
Каков наименьший уровень Н воды в сосуде, при котором металлический шар, перекрывающий круглое отверстие в вертикальной стенке, будет находиться в равновесии? Радиус металлического шара R. Относительная плотность шара δ. Диаметр отверстия d=1,5R.
| Вариант | ||||||||||||
| R, см | ||||||||||||
| δ | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 |
ЗАДАНИЕ 10.
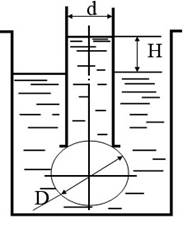
Погруженный в воду полый шаровой клапан диаметром D и массой m закрывает выходное отверстие внутренней трубы диаметром d = 2/3∙D. При какой разности уровней Н клапан начнет пропускать воду из внутренней трубы в резервуар?
| Вариант | ||||||||||||
| D, см | ||||||||||||
| m, кг | 0,06 | 0,1 | 0,15 | 0,25 | 0,35 | 0,5 | 0,7 | 1,0 | 1,4 | 2,0 | 2,7 | 3,6 |
ЗАДАНИЕ 11.
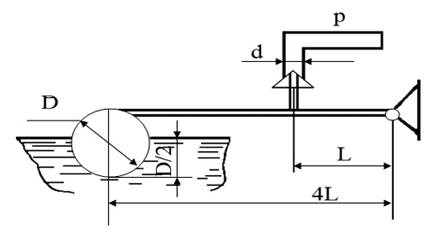
Наполнение бака контролируется поплавковым устройством. Определить диаметр шара-поплавка, при котором будет обеспечено закрытие подводящей трубы с избыточным давлением воды р. Шар изготовлен из листовой латуни толщиной δ=0,5 мм; плотность латуни 8400 кг/м3. Масса рычага mp = 60 г; масса запорной иглы mи=30 г.
| Вариант | ||||||||||||
| p, кПа | ||||||||||||
| d, мм |
ЗАДАНИЕ 12.
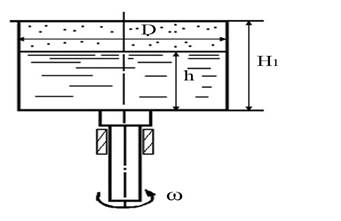
Замкнутый цилиндр размерами D и H0 заполнен водой до высоты h= 0,7∙H0 (в неподвижном состоянии) и вращается относительно вертикальной оси с угловой скоростью ω. Определить силу давления на крышку цилиндра при данной угловой скорости вращения, если давление над водой равно атмосферному.
| Вариант | ||||||||||||
| D, м | 0,6 | 0,6 | 0,7 | 0,7 | 0,8 | 0,8 | 0,9 | 0,9 | 1,0 | 1,0 | 1,2 | 1,2 |
| H0, м | 0,3 | 0,5 | 0,4 | 0,6 | 0,5 | 0,7 | 0,6 | 0,8 | 0,7 | 0,9 | 0,8 | 1,0 |
| ω,Рад\сек |
ЗАДАНИЕ 13.
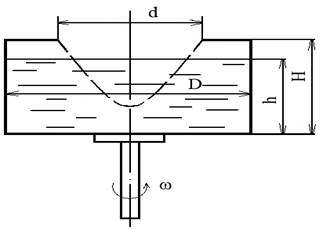
Цилиндрический сосуд с закраиной, имеющий диаметр D и высоту Н, предварительно заполнен водой до высоты h=0,8∙Н и вращается вокруг вертикальной оси. Диаметр закраины d=0,7∙D. Определить максимальную частоту вращения ω, при которой весь объем жидкости будет удерживаться в сосуде. Определить силу давления жидкости, действующую при этой угловой скорости вращения на закраину.
| Вариант | ||||||||||||
| D, м | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 |
| H, м | 0,3 | 0,35 | 0,4 | 0,5 | 0,6 | 0,7 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 |
| Вариант | ||||||||||||
| А | ||||||||||||
| α | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| В |
ЗАДАНИЕ 14.
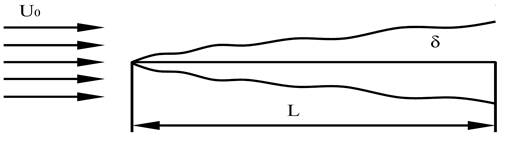
Пластина длиной L= 0,25 м обтекается потоком воды со скоростью U0 вдали от нее. Рассчитать и построить график изменения касательных напряжений на пластине и толщины пограничного слоя по всей ее длине, полагая течение плоским и критическое число РейнольдсаRee(кр) =4∙105. Определить силу сопротивления, действующую на пластину шириной В=4 м.
Как изменится толщина пограничного слоя в конце пластины и сила сопротивления, если степень турбулентности потока возрастет так, что критическое число Рейнольдса уменьшится вдвое?
| Вариант | ||||||||||||
| U0,м/с | 4,5 | 3,8 | 4,2 | 2,6 | 2,8 | 3,2 | 3,4 | 3,6 | 5,5 |
ЗАДАНИЕ 15.
Выявить закон нарастания толщины турбулентного пограничного слоя вдоль гладкой пластины при продольном обтекании ее безграничным потоком со скоростью U0 на бесконечности.






