1. Адиабатный процесс совершается, по определению, без теплообмена с окружающей средой, и описывает, в рамках нашей задачи, переход системы из 1-го во 2-е состояние.
Поэтому: 
. (2)
Уравнение (1), записанное для адиабатного процесса, имеет вид: 
(3)
Известно, что изменение внутренней энергии для любого термодинамического процесса:
.
Тогда, в нашем случае:
, (4)
где m –масса газа, 
- молярная теплоемкость при постоянном объеме, i=5 – число степеней свободы двухатомной молекулы, какой является молекула кислорода; R=8,31 Дж/(моль К) – молярная газовая постоянная; М = 
кг/моль – молярная масса кислорода.
Температуру Т2 найдем, используя уравнение Пуассона, описывающее адиабатный процесс:
,
где 
- показатель адиабаты.
Отсюда 
. (5)
После подстановки исходных данных получим Т2= 265 К.
Массу газа найдем из уравнения Менделеева – Клапейрона, записанного для состояния 1:
откуда 
(6)
Подстановка данных и расчет дает массу газа m=0,0055 кг.
Из уравнения Менделеева – Клапейрона для состояния 2 найдем давление р2:
.
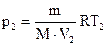После подстановки в это уравнение выражения для массы (6) получим:
.
Подстановка данных и расчет приводят к результату р2=0,189 
Па.
Определили термодинамические параметры для состояния 2:
р2=0,189 Па, V2= 2.10 
м 
, T2=265 К.
Подставив выражения для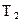 
, m и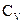 
в уравнение (4), получим
. (7)
Подстановка в (7) численных значений приводит к результату:
Дж.
Из (3) следует: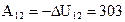 
Дж.
Итак, для адиабатного процесса, переводящего систему из состояния 1 в состояние 2, получили: Дж, Дж, 
Дж.
2. Изобарный процесс характеризуется постоянством давления. Для этого процесса первое начало термодинамики имеет вид:
.
При изобарном расширении (в нашей задаче это переход из состояния 2 в состояние 3) работа газа, по определению, равна:
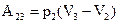, (8)
где р2=0,189 Па=const. Из условия задачи известны V2 и V3. Подстановка численных значений в формулу (8) дает
А23=189 Дж.
Температуру 
найдем, воспользовавшись законом Гей - Люссака для изобарного процесса: 
.
Отсюда: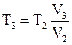 
=397 К.
Отметим, что так как процесс 
- изобарный, следовательно, р2=р3.
Определили термодинамические параметры для состояния 3:
Па, 
м , T3=397 К.
Изменение внутренней энергии газа рассчитаем по уже известной формуле:
. (9)
Количество теплоты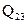 
, полученное газом в изобарном процессе, найдем согласно (1):
(10)
Итак, для изобарного процесса, переводящего систему из состояния 2 в состояние 3, получили: A 
=189 Дж;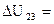 
471 Дж; 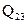=660 Дж.
3. Изотермический процесс характеризуется постоянством температуры. Для этого процесса первое начало термодинамики имеет вид:
,
так как при постоянной температуре внутренняя энергия системы не изменяется, то есть 
.
Следовательно, при изотермическом изменении объема (в нашей задаче это переход из состояния 3 в состояние 4) количество полученной газом теплоты будет совпадать с работой газа, которая, в свою очередь, равна:
. (11)
Определим параметры 4-го состояния: Т4=Т3, так как процесс - изотермический, V4=2V3 – по условию. Давление кислорода p4 найдем из закона Бойля – Мариотта,:
.
Отсюда: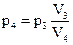 
. Подстановка числовых данных и расчет приводят к результату: p4= 
Па.
Таким образом, термодинамические параметры 4 – го состояния: р4= Па, V4= 6.10 м , T4=397 К.
Теперь, когда известны все необходимые данные, проведем расчет по формуле (11) и получим: 
393 Дж.
Для изотермического процесса, переводящего систему из состояния 3 в состояние 4, получили: A34=393 Дж;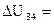 
0; Q34=393 Дж.
4. Изохорный процесс. Характеризуется неизменностью объема, занимаемого газом. Так как, по определению, работа газом совершается только при изменении его объема, то для изохорного процесса она равна нулю. Это значит, что первое начало термодинамики имеет вид: 
.
Или, в наших обозначениях: 
.
Следовательно, при изохорном процессе количество подведенной к газу теплоты будет совпадать с изменением его внутренней энергии, которое, в свою очередь, равно:
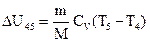. (12)
Определим параметры 5-го состояния: Т5=Т4+150=547 К – по условию задачи. Процесс - изохорный, следовательноV5=V4 =6.10 м . Давление кислорода p5 найдем из закона Шарля:
.
Отсюда: 
Па.
Таким образом, термодинамические параметры 5 – го состояния: р5=0,136 
Па, V5= 6.10 м 
, T4=547 К.
Проведя уже стандартный расчет по формуле (12) получим:
.
Итак, для изохорного процесса, переводящего систему из состояния 4 в состояние 5, получили: A45=0; 
536 Дж; Q45=536 Дж.
Пример 10. Определить изменение энтропии при изотермическом расширении кислорода массой 10 г от объема V1=25 л до объема V2=100 л.
Решение
По определению, изменение энтропии при переходе системы из состояния 1 в состояние 2 равно:
.
Найдем этот интеграл с учетом того, что по условию задачи процесс протекал изотермически (T – const). Тогда
, (1)
где Q12 - количество теплоты, полученное газом при переходе из состояния 1 в состояние 2. Определим его, используя первое начало термодинамики:
.
Для изотермического процесса изменение внутренней энергии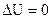 
, следовательно, 
. (2)
Известно, что работа газа А при изотермическом расширении равна:
. (3)
С учетом (2) и (3) равенство (1) примет вид:
. (4)
Подставив в (4) численные значения и произведя вычисления, получим:
Дж/К.
Контрольная работа № 1
Таблица выбора вариантов индивидуального задания
| Вариант | Номера задач | |||||||||
1. При прямолинейном движении зависимость пройденного телом пути от времени описывается уравнением S=A+Bt+Ct2+Dt3, где В=2 м/с , С=0,14 м/с2, D=0,1 м/с3. Через сколько времени после начала движения ускорение тела будет равно а) 1 м/с2; б) 6 м/с2? Чему равна средняя скорость тела за промежуток времени, в течение которого ускорение возросло от 1 м/с2 до 6 м/с2?
2. Зависимость координаты тела от времени задана уравнением x=At+Bt2+Ct3, где A=12 м/c, B=-3 м/с2, C=-4 м/c3. Найти в явном виде зависимость скорости и ускорения от времени; расстояние, пройденное телом, мгновенные скорость и ускорение тела через 2 секунды после начала движения; среднюю скорость за промежуток времени от t1=2c до t2=5с.
3. Две материальные точки движутся согласно уравнениям: x1=A1t+B1t2+C1t3; x2=A2t+B2t2+C2t3, где А1=4 м/с, В1=8 м/с2, С1=-16 м/с3; А2=2 м/с, В2=-4 м/с2, С2=1 м/с3. В какой момент времени ускорения этих точек будут одинаковы? Найти скорости точек в этот момент. Найти среднюю скорость второй материальной точки за промежуток времени с момента начала движения до момента равенства их ускорений.
4. Движения двух материальных точек выражаются уравнениями: x1=A1t+B1t2+C1t3; x2=A2t+B2t2+C2t3, где А1=20 м/с, В1=2 м/с2, С1= -4 м/с3; А2=2 м/с, В2=2 м/с2, С2=0,5 м/с3. В какой момент времени скорости этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента равенства их скоростей.
5. Движение материальной точки задано уравнением x=Аt+Вt2, где А=4 м/с, В=-0,05 м/с2. Определить момент времени, в который скорость точки равна нулю. Найти путь, пройденный точкой, координату и ускорение точки в этот момент. Найти среднюю скорость точки за промежуток времени с момента начала движения до момента равенства ее скорости нулю.
6. Движения двух материальных точек выражаются уравнениями:x1=A1+B1t2+C1t3; x2=A2t+B2t2+C2t3, где А1=-12 м, В1=-2 м/с2, С1= 8 м/с3; А2=-4 м/с, В2=-3 м/с2, С2=8 м/с3. В какой момент времени координаты этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента равенства их координат.
7. Уравнение движения тела имеет вид х=15t - 0,4t2. Определить промежуток времени после начала движения, в течение которого точка вернется в исходное положение. Найти путь, пройденный точкой и ее среднюю скорость за этот промежуток времени.
8. Уравнение движения материальной точки по прямой имеет вид х=А+Вt+Сt2, где А=4 м, В=2 м/с, С=-0,5 м/с2. Для момента времени t1=2 секунды определить координату точки и мгновенное ускорение. Найти путь, пройденный точкой, и среднюю скорость за промежуток времени от t1=2с до t2=6с.
9. Зависимость пройденного телом пути от времени дается уравнением S=A-Bt+Ct2+Dt3, где А=6 м, В=3м/с, С=-2 м/с2, D=0,2 м/с3. Считая движение прямолинейным, определить для тела в интервале времени от t1=1 c до t2=4 с 1) среднюю скорость; 2) путь, пройденный телом; 3) в какой момент времени после начала движения точка вернется в исходное положение?
10. Две материальные точки движутся согласно уравнениям:x1=A1t +C1t3; x2=A2t+B2t2+C2t3, где А1=14 м/с, С1=-6 м/с3; А2=2 м/с, В2=4 м/с2, С2=-5 м/с3. В какой момент времени t1 ускорение первой точки будет вдвое больше ускорения второй? Найти скорости точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента времени t1.
11. Тело некоторой массы скользит вниз по наклонной плоскости с постоянным ускорением, равным 0,05g. Найти угол наклона этой плоскости, если коэффициент трения равен 0,02.
12. За какое время тело спустится с вершины наклонной плоскости высотой 3 м и углом у основания 
, если максимальный угол у основания наклонной плоскости, при котором тело находится на ней в покое, равен 
?
13. Тело массой m скользит по наклонной плоскости, образующей с горизонтом угол 45 
. Зависимость пройденного телом пути от времени дается уравнением s=Ct2, где С=1,73 м/с 
. Найти коэффициент трения тела о плоскость.
14. На автомобиль массой 1т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с ускорением 1 м/с2 в гору с уклоном 1 м на каждые 25 м пути.
15. По наклонной плоскости с углом 
наклона к горизонту, равным 30 , скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения 
=0,15.
16. С каким ускорением будет скользить тело по наклонной плоскости, образующей с горизонтом угол =24 , если коэффициент трения равен 0,03? Какое время потребуется для прохождения при этих условиях пути 100 м? Какую скорость тело будет иметь в конце пути?
17. С вершины клина, длина которого l=2 м и высота h=1 м, начинает скользить небольшое тело. Коэффициент трения между телом и клином =0,15. Определить: 1) ускорение, с которым движется тело; 2) время прохождения тела вдоль клина; 3) скорость тела у основания клина.
18. На автомобиль массой 2т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью в гору с уклоном 1 м на каждые 25 м пути.
19. Тело некоторой массы равномерно скользит вниз по наклонной плоскости. Найти угол наклона этой плоскости, если коэффициент трения равен 0,05.
20. Тело скользит по наклонной плоскости, образующей с горизонтом угол 45 . Пройдя путь 36,4 см, тело приобретает скорость 2 м/с. Найти коэффициент трения тела о плоскость.
21. Маховик, момент инерции которого равен J=63,7 
, вращается с постоянной угловой скоростью 
=31,4 рад/с. Найти тормозящий момент М, под действием которого маховик останавливается через t=20 с. Маховик считать однородным диском.
22. Определить, какая постоянная касательная сила приложена к ободу однородного сплошного диска радиусом 0,5 м и массой 24 кг, если при вращении на него действует момент сил трения 2 
. Угловое ускорение диска постоянно и равно 16 рад/ 
.
23. Маховое колесо, имеющее момент инерции 245 , вращается, делая 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти момент сил трения.
24. К ободу однородного сплошного диска радиусом R=0,2 м приложена постоянная касательная сила F=98,1 Н. При вращении на диск действует момент сил трения 5 . Найти массу диска, если известно, что диск вращается с постоянным ускорением 
=100 рад/ .
25. Маховик в виде сплошного диска, момент инерции которого J=150 , вращается с частотой 
=240 об/мин. Через время t=1 мин как на маховик стал действовать момент сил торможения, он остановился. Определить момент сил торможения.
26. Вал массой m=100 кг и радиусом R 5 см вращался с частотой =8 
. К цилиндрической поверхности вала прижали тормозную колодку с силой N=40 Н, под действием которой вал остановился через t=10 с. Определить коэффициент трения.
27. Диск массой m=2 кг и радиусом R=10 см вращается вокруг оси, проходящей через его центр. Уравнение движения диска имеет вид 
, где 
. Определить вращающий момент М в момент времени t=2 с, если момент сил торможения постоянен и равен 12 .
28. Маховик радиусом 0,5 м, вращаясь равнозамедленно, за 10 секунд изменил частоту вращения от 480 до 120 об/мин. Тормозящий момент постоянен и равен 40 . Определить массу маховика.
29. К шару радиусом 0,2 м приложена касательная сила 100 Н. При вращении вокруг оси, проходящей через центр масс, на шар действует момент сил трения 5 . С каким угловым ускорением вращается шар, если его масса 15 кг?
30. Маховик в виде сплошного диска, момент инерции которого J=1,5 , вращаясь при торможении равнозамедленно, за время t=1 мин уменьшил частоту своего вращения с 
=240 об/мин до 
=120 об/мин. Определить момент силы торможения.
31. На нитях одинаковой длины, равной 2,5 м, закрепленных в одной точке, подвешены два шарика массами 75 г и 100 г, соответственно. Нить с большим шариком отклонили на угол 60 градусов и отпустили. Считая удар абсолютно неупругим, определить, на какую высоту поднимутся шарики после соударения.
32. Пуля массой 15 г, летящая с горизонтальной скоростью 0,5 км/с, попадает в баллистический маятник1) массой 6 кг и застревает в нем. Определить высоту, на которую поднимется маятник, откачнувшись после удара.
33. Два тела массами 3 кг и 5 кг движутся навстречу друг другу со скоростями 7 м/с и 9 м/с. Найти скорость движения тел после соударения и выделившуюся при неупругом ударе энергию.
34. Пуля массой 15 г, летящая горизонтально со скоростью 200 м/с, попадает в баллистический маятник1) длиной 1 м и массой 1,5 кг и застревает в нем. Определить угол отклонения маятника.
35. Тело массой 3 кг движется со скоростью 2 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе.
36. Пуля массой 12 г, летящая с горизонтальной скоростью 0,6 км/с, попадает в мешок с песком массой 10 кг, висящий на длинной нити, и застревает в нем. Определить: 1) высоту, на которую поднимется мешок, отклонившись после удара; 2) энергию, израсходованную на пробивание песка.
37. На нитях одинаковой длины, равной 0,8 м, закрепленных в одной точке, подвешены два шарика массами 40 г и 60 г, соответственно. Нить с меньшим шариком отклонили на угол 60 градусов и отпустили. Считая удар неупругим, определить, какая энергия пошла на нагревание шариков.
38. Пуля массой 9 г, летящая с горизонтальной скоростью 0,6 км/с, попадает в баллистический маятник1) массой 8 кг и застревает в нем. Определить выделившуюся при этом энергию.
39. Тело массой 8 кг движется со скоростью 3 м/с и ударяется о движущееся со скоростью 1 м/с в том же направлении тело вдвое большей массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе.
40. На нитях одинаковой длины, равной 1,2 м, закрепленных в одной точке, подвешены стальной и пластилиновый шарики одного размера массой 20 г и 8 г, соответственно. Нить со стальным шариком отклонили на угол 45 градусов и отпустили. Определить, на какую высоту поднимутся шарики после соударения.
41. Частица движется со скоростью v=0,8c, где с – скорость света в вакууме. Определить: 1) отношение массы релятивистской частицы к ее массе покоя; 2) релятивистский импульс и полную энергию, если эта частица – электрон.
