Примеры решения задач
Пример 1. Кинематическое уравнение движения материальной точки по прямой имеет вид 
, где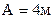 
, 
, 
. Для момента времени 
определить: 1) координату 
точки; 2) мгновенную скорость 
; 3) мгновенное ускорение 
; 4) среднюю скорость за промежуток времени с момента начала движения до .
Решение
1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения заданное значение времени 
:
.
Подставив в это выражение значения постоянных А, В, С, и , произведем вычисления: 
.
2. Уравнение, описывающее зависимость скорости от времени, найдем, продифференцировав координату 
по времени: 
. Тогда в заданный момент времени мгновенная скорость 
.
Подставим сюда значения В, С, и произведем вычисления:
.
Знак минус в полученном значении скорости указывает на то, что в данный момент времени скорость материальной точки направлена в сторону, противоположную положительному направлению оси X.
3. Функциональную зависимость ускорения от времени найдем, используя определение ускорения, как второй производной от координаты по времени:
.
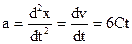Подставим значения С, 
и произведем вычисления
.
4. По определению, среднее значение скорости равно: 
, где S – путь, пройденный точкой за время 
.
Если в течение рассматриваемого промежутка времени скорость точки не изменяется по направлению, то
,
где x(t1) и x(t0) – координаты материальной точки в конечный и начальный моменты времени, соответственно.
В нашем случае в начальный момент времени 
с скорость точки равна 2 м/с, а в момент времени скорость - . Следовательно, в некоторый момент времени 
скорость точки обращается в нуль, т.е. в этот момент времени материальная точка изменяет направление своего движения. Тогда весь путь, пройденный точкой, можно представить в виде: 
, где 
- путь, пройденный точкой до остановки, а 
- путь, пройденный в обратном направлении.
Найдем момент времени, в который скорость точки равна нулю: 
.
Отсюда 
. Подставив численные значения, получим: =1,155 с.
Тогда 
=7,08 м,
=4 м,
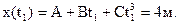
Cледовательно, S=(7,08-4)+(7,08-4)=6,16 м, средняя скорость <v> =3,08 м/с.
Пример 2. Тело массой 10 кг движется вверх по наклонной плоскости. На тело действует сила F=100 Н, направленная вверх под углом 
= 
к поверхности наклонной плоскости. Коэффициент трения 
=0,1. Угол наклона плоскости 
= . Определить ускорение, с которым движется тело.
Решение
При движении тела кроме силы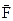 
на него действуют также: сила тяжести - 
, сила реакции опоры - 
и сила трения - 
, показанные на рисунке.
Ускорение тела определим, используя основной закон динамики, который в векторной форме в условиях данной задачи имеет вид:
(1)
Направим ось X вдоль наклонной плоскости в сторону движения тела, а ось Y - перпендикулярно к ней.
Запишем уравнение (1) в проекциях на выбранные оси координат.
На ось X: 
(2)
на ось Y: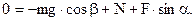 
(3)
По определению силы трения: 
.
Силу реакции опоры найдем из уравнения (3):
.
Тогда 
.
Подставим это выражение в (2) и получим рабочую формулу: 
.
Проведя подстановку данных и вычисления, найдем: а=3,3м/с2.
Пример 3. К ободу однородного диска радиусом 0,2 м, вращающегося вокруг своей оси, приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения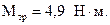 
Найти массу диска, если известно, что диск вращается с угловым ускорением 
=100 
.
Решение
Известно, что момент инерции диска относительно оси, проходящей через его центр, равен: 
.
Отсюда масса диска: 
(1)
Воспользовавшись законом динамики вращательного движения твердого тела, найдем момент инерции J:
, (2)
где М - результирующий момент сил, под действием которого вращается диск. Запишем уравнение (2) в проекции на ось вращения (с учетом направлений моментов).
. (3)
Здесь 
– момент силы F относительно оси вращения.
Подставляя (2) и (3) в (1), находим:
.
Проведя необходимые расчеты, получим: m=7,36 кг.
Пример 4. Два свинцовых шара массами 
=2 кг и 
=3 кг подвешены на нитях длиной L=70 см. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на угол 
и отпустили. Считая удар центральным и неупругим, определить: 1) высоту h, на которую поднимутся шары после удара; 2) энергию 
, израсходованную на деформацию шаров при ударе.
Решение
Проведем анализ движения тел в данной задаче. Движение шаров можно разбить на три этапа.
На первом этапе (до соударения) шар массой m1 движется под действием только консервативных сил (сила трения отсутствует). Следовательно, на этом участке движения выполняется закон сохранения механической энергии:
, (1)
где 
- начальная высота, на которой находился отклоненный шар, - скорость этого шара непосредственно перед ударом.
Второй этап – неупругое соударение шаров, при котором выполняется закон сохранения импульса:
,
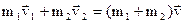где 
и 
- скорости шаров до удара, 
- скорость шаров, движущихся как единое целое, непосредственно после удара.
С учетом того, что 
, получим:
. (2)
Из уравнения (2) очевидно, что скорость шаров сразу после удара будет направлена вдоль оси Х, так же как и скорость первого шара непосредственно перед соударением. Поэтому, уравнение (2) в проекциях на ось Х будет иметь вид:
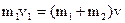. (3)
На третьем этапе движения шаров после удара снова выполняется закон сохранения механической энергии:
. (4)
Отсюда искомая высота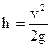 
.
Используя уравнения (3) и (1), получим: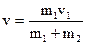 
,
.
Тогда 
.
Энергия, израсходованная на деформацию шаров при ударе:
. (5)
Проведя подстановку и преобразования, получим:
.
Вычислим: 1) h=0,056 м; 2) =4,12 Дж.
Пример 5. Кинетическая энергия Ек электрона равна 
. Определить скорость электрона, его релятивистские массу и импульс, а также полную энергию.
Решение
Кинетическая энергия релятивистской частицы равна:
, (1)
где 
- полная энергия, 
- энергия покоя частицы (в нашем случае – электрона), 
кг - масса покоя электрона; 
- его релятивистская масса, 
, 
м/с - скорость света.
Последовательная подстановка этих величин в (1) приводит нас к формуле:
.
Выполнив преобразования относительно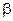 
, найдем скорость частицы, выраженную в долях скорости света 
:
. (2)
Расчет энергии покоя дает величину:
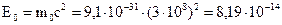(Дж).
Подставив числовые значения 
и Ек в формулу (2), получим 
.
Так как 
, то получим: 
.
Найдем релятивистские массу m, импульс p и полную энергию Е:
кг,
Дж.
Пример 6. Материальная точка массой 5 г совершает гармонические колебания с частотой 0,5 Гц вдоль оси Х. Амплитуда колебаний 3 см. Определить: 1) скорость точки в момент времени, когда смещение х=1,5 см; 2) максимальную силу, действующую на точку.
Решение
1. Уравнение гармонического колебания имеет вид:
. (1)
По определению, скорость точки равна первой производной по времени от смещения:
. (2)
Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого возведем оба уравнения в квадрат:
, (3)
. (4)
Из уравнений (3) и (4) выразим 
, 
. Воспользовавшись известным соотношением 
, получим:
.
Так как 
, тогда
.
Решая последнее уравнение относительно v, найдем:
.
Вычисляя, получим v=±8,2 м/с.
Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси Х, знак минус - когда направление скорости противоположно.
2. Силу, действующую на точку, найдем, используя второй закон Ньютона:
F = ma, (3)
где а - ускорение точки.
По определению:
или: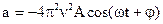 
.
Подставим это выражение в (3) и получим:
.
Отсюда максимальное значение силы
(при 
):
.
Подставим в это уравнение значения величин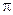 
, 
, m, А и найдем 
.
Пример 7. На концах тонкого стержня длиной 1 м и массой М=400г укреплены шарики малых размеров массами m1=200 г и m2=300 г. Стержень колеблется около горизонтальной оси, перпендикулярной стержню и проходящей через его середину (точка О на рис.). Определить период колебаний, совершаемых стержнем.
Решение
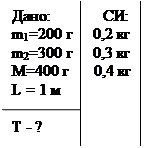
Период колебаний физического маятника, каковым является стержень с шариками, определяется соотношением:
, (1)
где J - момент инерции маятника относительно оси колебаний; m - его масса; а - расстояние от центра масс маятника до оси колебаний.
В силу аддитивности, момент инерции данного маятника равен сумме моментов инерции J1 и J2 шариков и стержня J3:
J = J1+J2+J3. (2)
Принимая шарики за материальные точки, запишем их моменты инерции: 
; 
.
Так как ось проходит через середину стержня, то его момент инерции относительно этой оси 
. Подставив полученные выражения J1, J2 и J3 в формулу (2), найдем общий момент инерции физического маятника:
.
Произведя вычисления по этой формуле, найдем J = 0,158 
.
Масса маятника состоит из масс шариков и массы стержня:
m = m1+m2+М = 0,9 кг.
Расстояние от центра масс маятника до оси колебаний найдем, исходя из следующих соображений. Если ось Х направить вдоль стержня и начало координат совместить с точкой О, то искомое расстояние равно координате центра масс маятника 
, т.е.
,
или 
.
Подставив значения величин m1, m2, m, L и произведя вычисления, найдем: а= 
м.
Произведя расчет по формуле (1), получим период колебаний физического маятника: Т=3,57 с.
Пример 8. В баллоне объемом 10 литров находится гелий под давлением 1 МПа при температуре 300 К. После того как из баллона был израсходован гелий массой 10 г, температура в баллоне понизилась до 290 К. Определить 1) давление гелия, оставшегося в баллоне; 2) его плотность; 3) количество оставшихся в баллоне молекул гелия; 4) их концентрацию.
Решение
1. Воспользуемся уравнением Менделеева – Клапейрона, применив его к начальному и конечному состояниям газа:
;
.
Выразим из этих уравнений массы m1 и m2 гелия и найдем их разность:
; 
.
.
Из последнего уравнения выразим искомое давление:
.
Молярная масса гелия (Не) равна 
кг/моль, R=8,31 Дж/(моль К) – молярная газовая постоянная.
Подставив данные и проведя расчет, найдем давление
=364 103 Па.
2. Плотность вещества, по определению, равна 
. Выразим эту величину из исходного уравнения для второго состояния системы:
.
После подстановки данных и проведения расчета получим:
кг/м3.
3. Количество молекул, оставшихся в баллоне, равно: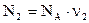 
, где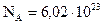 
моль-1 – число Авогадро. Количество вещества 
, оставшегося в баллоне газа, выразим из уравнения Менделеева – Клапейрона для второго состояния системы:
.
Тогда, искомое число молекул:
.
После подстановки данных и проведения расчета получим:
.
4. Концентрация молекул по определению равна: 
, тогда:
.
После подстановки данных и проведения расчета получим:
.
Пример 9. Кислород, находящийся в состоянии 1 при давлении 
=0,5 МПа, температуре 
=350 К и занимающий объем 
=1л, перевели в состояние 2, подвергнув адиабатическому расширению до объема 
=2 л. Затем изобарно объем газа был увеличен до 
=3 л. В состояние 4 кислород был переведен путем изотермического увеличения объема в два раза. После этого последовал изохорный нагрев на 
= 150К, который перевел газ в пятое состояние. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
Решение
Согласно первому началу термодинамики, количество теплоты Q, полученное газом, расходуется на изменение внутренней энергии газа (
) и совершение газом работы (А) против внешних сил:
. (1)
Параметры состояния 1 известны из условия задачи: 
=0,5 
Па, 
= 1.10 
м 
, 
=350 К.
