Варианты 1, 2
В магазин поступило n телевизоров. Из них k имеют скрытые дефекты. Покупателю для выбора наудачу предложено l телевизоров. Какова вероятность того, что все предложенные покупателю изделия не содержат дефектов?
1. n=30, k=3, l=2.
2. n=20, k=2, l=3.
Варианты 3,4
Из партии, содержащей n изделий, среди которых k бракованных, наудачу извлекают m изделий для контроля. Найти вероятности следующих событий: А={в полученной выборке ровно l бракованных изделий}, B={в полученной выборке нет бракованных изделий}.
3. n=10, k=3, l=1, m=3.
4. n=12, k=3, l=2, m=3.
Варианты 5,6
Имеются два ящика с деталями. В первом n деталей, из них m годных. Во втором ящике N изделий, из них M годных. Сборщик наудачу выбрал по одной детали из каждого ящика. Найти вероятность того, что обе выбранные детали годные. Какова вероятность того, что обе выбранные детали бракованные?
5. n=12, m=8, N=8, M=7.
6. n=14, m=10, N=6, M=4.
Варианты 7,8
Группа, состоящая из 8 человек, занимает места с одной стороны прямоугольного стола. Найти вероятность того, что 2 определенных лица окажутся рядом, если:
7. число мест равно 8.
8. число мест равно 12.
Варианты 9,10
Из урны, содержащей m+n шаров, из которых m белых и n черных, на удачу отбирают k шаров и откладывают в сторону. Найти вероятности следующих событий: A={все отложенные шары белые}, B={среди отложенных шаров ровно l белых}.
9. m=10, n=6, k=5, l=3.
10. m=8, n=12, k=6, l=4.
Задача № 4
(Вероятности сложных событий. Применение теорем сложения и умножения)
Электрическая цепь прибора составлена по схеме, приведенной на рисунке Вашего варианта. Событие Ak={k-ый элемент безотказно работает}. k=1,2,…,6. Отказы элементов являются независимыми в совокупности событиями. Известна надежность  k-го элемента (вероятность безотказной работы). Соответственно
k-го элемента (вероятность безотказной работы). Соответственно  - вероятность отказа.
- вероятность отказа.
События А ={цепь работает}, B={разрыв цепи}. Выразить события А и B в алгебре событий Ak. Найти вероятность отказа прибора и вероятность надежности схемы. p1=p2=0.9, p3=p4=0.8, p5=p6=0.85.
Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6

Вариант 7
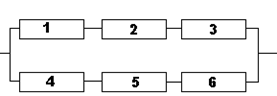
Вариант 8

Вариант 9

Вариант 10

Задача №5
(Операции над событиями. Полная вероятность. Формула Байеса)
Вариант 1. В цеху - три независимо работающих линии. Вероятности того, что в случайный момент времени загружены: 1-ая линия равна 0,9; вторая - 0,8; третья - 0,7. Найти вероятности того, что в случайный момент времени:
А- загружены две линии;
В- хотя бы одна линия свободна;
С- все линии свободны.
Вариант 2. На станции технического обслуживания автомобилей работают две бригады: в первой - 8 "механиков, во второй - 5. Вероятность того, что автомобиль, попавший в первую бригаду, будет обслужен отлично, равна 0,8, а во вторую - 0,9. Прибывший на станцию автомобиль был обслужен отлично. Найти вероятность того, что им занималась первая бригада.
Вариант 3. Разгрузочно-погрузочная станция содержит три линии обслуживания. Вероятности осуществить погрузку в течение часа равны: для 1-й линии - 0,8, для 2-й - 0,7, для 3-й - 0,9. Одновременно на погрузку прибыли три вагона. Найти вероятности того, что в течение часа:
А- все три вагона будут загружены;
В- будут загружены не менее двух вагонов;
С - будет загружен хотя бы один вагон.
Вариант 4. Завод имеет 70% технологических линий 1-го типа и 30% линий 2-го типа. Если деталь попадет на линию 1-го типа, то вероятность брака равна 0,1, для линии 2-го типа - 0,2. Найти вероятность того, что случайно выбранная деталь окажется бракованной.
Вариант 5. Цех имеет три независимо работающих конвейерные линии. Вероятности сбоя в работе в течение часа: для 1-й линии - 0,1, для 2-й - 0,05, для 3-й - 0,08. Найти вероятности того, что в течение часа:
А- ни на одной из линий сбоя не произойдет;
В- сбой произойдет не более чем на одной линии;
С - сбой произойдет точно на одной линии.
Вариант 6. Система контроля за качеством представляет собой 7 аппаратов первого вида и 4 аппарата второго вида. Каждая деталь случайным образом попадает на проверку в один из аппаратов. Аппарат первого вида обнаруживает бракованную деталь с вероятностью 0,8, а второго вида - 0,9. Бракованная деталь была обнаружена. Найти вероятность того, что она проходила проверку аппаратом первого вида.
Вариант 7. Станция скорой медицинской помощи небольшого микрорайона имеет три реанимационные бригады. Вероятность того, что в любой момент времени заняты: 1-я бригада равна 0,5, 2-я - 0,6, 3-я - 0,7. Найти вероятность того, что в случайно выбранный момент времени:
А- все бригады заняты;
В- хотя бы одна бригада свободна;
С- свободны две бригады из трех.
Вариант 8. На АЗС три линии обслуживания. На 1-й линии 2 заправочные колонки, на 2-й - 4, на 3-й - 3. Если автомобиль подъедет к 1-й линии, то вероятность заправиться в течение 15 минут равна 0,9, если подъедет ко 2-й, то эта вероятность - 0,75, если к 3-й, то - 0,8. Найти вероятность того, что автомобиль, подъехавший к АЗС заправится в течение 15 минут.
Вариант 9. В речном порту - три причала. Вероятности того, что причал занят равны: для 1-го причала - 0,9, для 2-го - 0,8, для 3-го - 0,7. Найти вероятности того, что в случайный момент времени: А- все три причала заняты; В- занят только один причал; С- хотя бы один причал свободен.
Вариант 10. На разгрузочно-погрузочной станции два железнодорожных пути. Вероятность того, что вагон попадет на 1-й путь, равна 0,55, на 2-й - 0,45. Вероятность того, что вагон будет разгружен в течение 30 минут равна 0,9, если он окажется на первом пути и 0,8, если на втором. Доставленный на станцию вагон был разгружен в течение 30 минут. Найти вероятность того, что вагон обслуживался на первом пути.
Вариант 11. В аэропорту три взлетно-посадочные полосы. Вероятности того, что взлетно-посадочные полосы свободны, равны: для 1-й полосы - 0,8, для 2-й - 0,7, для 3-й - 0,6. Найти вероятности событий:
А- хотя бы одна взлетно-посадочная полоса свободна;
В- свободны точно две полосы;
С - все полосы заняты.
Вариант 12. Детали изготавливаются на двух заводах, причем первый завод выпускает 60%, а второй 40%. Вероятность того, что деталь окажется бракованной, равна 0,1, если сделана на первом заводе и 0,05, если на втором. Найти вероятность того, что наудачу взятая деталь окажется качественной.
Вариант 13. Телефонная станция обслуживает три микрорайона города. Вероятность того, что в течение суток произойдет сбой в 1-м микрорайоне, равна 0,1, во 2-м -0,15, в 3-м- 0,12. Найти вероятности того, что в течение суток:
А- ни в одном микрорайоне не произойдет сбой;
В- сбой произойдет не более чем в одном микрорайоне;
С - сбой произойдет точно в одном микрорайоне.
Вариант 14. На АЗС три линии обслуживания. На 1-й линии 2^ заправочные колонки, на 2-й - 4, на 3-й - 2. Если автомобиль подъедет к 1-й линии, то вероятность заправиться в течение 15 минут равна 0,9, если подъедет ко 2-й, то эта вероятность - 0,7, если к 3-й, то - 0,8. Найти вероятность того, что автомобиль, подъехавший к АЗС, заправится в течение 15 минут.
Вариант 15. Конвейер содержит три одинаковые, независимо работающие линии. Вероятность того, что в данный момент времени занята каждая линия, равна 0,8. Найти вероятности того, что в случайный момент времени: А- свободна хотя бы одна линия; В- свободны точно две линии; С - все линии заняты.
Вариант 16. По военному объекту производится пуск двух ракет. Вероятность попадания в него первой ракеты равна 0,75, второй ракеты - 0,85.^ Вероятность уничтожения объекта при попадании в него одной ракеты равна 0,5,. а при попадании двух ракет - 0,95. В результате пуска обеих ракет объект был уничтожен. Найти вероятность того, что в объект попала лишь одна бомба.
Вариант 17. Три стрелка производят по одному выстрелу. Вероятности попадания для каждого стрелка соответственно равны: 0,7, 0,85 и 0,8. Найти вероятности того, что:
А- попали точно два стрелка;
В- попал хотя бы один стрелок;
С- попали не менее двух стрелков.
Вариант 18. Корабль, атакованный подводной лодкой, был потоплен одной торпедой. Вероятность попадания торпеды в носовую часть корабля - 0,25, в среднюю - 0,4, в кормовую - 0,35. Вероятности потопления корабля при попадании торпеды в каждую из его частей соответственно равны: 0,4, 0,9 и 0,5. Найти вероятность того, что торпеда попала в корму.
Вариант 19. Три охотника отправились "на кабана". Вероятности заполучить добычу для них соответственно равны 0,4, 0,6 и 0,7. Найти вероятности того, что:
А- все три охотника вернулись с добычей;
В- хотя бы один охотник вернулся с добычей;
С- не более одного охотника вернулись с добычей.
Вариант 20. Строительная компания, в которой два управления, ведет застройку микрорайона. Вероятности того, что наудачу взятый объект, выполняемый первым управлением, будет сдан в эксплуатацию досрочно, равна 0,7, вторым -0,8. Первое управление выполняет 65% всех работ, второе - 35%. Найти вероятность того, что наудачу «взятый объект микрорайона будет сдан в эксплуатацию досрочно.
Задача №6 (Дискретные случайные величины)
Составить закон распределения случайной величины Х. Записать функцию распределения, построить её график. Вычислить числовые характеристики М(Х), D(Х), s(Х)).
Варианты №1,2,3,4
Х-число отказавших элементов в одном опыте с устройством, состоящим из n независимо работающих элементов. Вероятность отказа каждого элемента р.
1. n=3, p=0.1.
2. n=4, p=0.15.
3. n=3, p=0.15.
4. n=4, p=0.2.
Варианты №5,6,7
В партии k% бракованных изделий. Наудачу отобрано n изделий. Х- число бракованных изделий среди отобранных. Дискретная случайная величина Х распределена по биномиальному закону:
5. k=15%, n=4.
6. k=10%, n=5.
7. k=20%, n=3.
Варианты №8,9,10
В партии из n деталей имеется m стандартных. Наудачу отобрали k деталей. Х-число стандартных деталей среди отобранных.
8. n=10, m=8, k=3.
9. n=9, m=7, k=3.
10. n=12, m=10, k=3.
Задача № 7 (Выборка, выборочные характеристики)
Из изучаемой налоговыми органами обширной группы населения случайным образом отобраны 10 человек и собраны сведения об их доходах за истекший год в тысячах рублей: х1, х2,…, х10. Найти выборочное среднее, исправленную выборочную дисперсию. Считая распределение доходов в группе нормальным и принимая в качестве его параметров выборочные характеристики, определить, какой процент населения имеет годовой доход, превышающий 70 тыс. рублей.
| № вар | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 |






