Тр. №5. Дифракция – задача 8 Чопчица (пункты 1 – 4, 8), тепловое излучение – пункт 9 «Проектируем электролампочку».
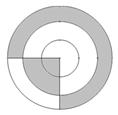Между источником S монохроматического света с длиной волны λ и точкой наблюдения P находится препятствие, форма которого показана на рисунке 1. Прямая SP проходит через центр системы окружностей на рисунках. Расстояние от источника до препятствия равно a, расстояние от препятствия до точки наблюдения равно b. Радиусы окружностей R1, R2, R3 заданы в количествах, заключенных в них зон Френеля.
| λ, нм | а, м | b, м | R1, зон | R2, зон | R3, зон | h, мкм | n | ϕ, град | а1, мкм | b1, мкм | c1, мкм | N1 мм-1 | L, м |
| 1,30 | 1,40 | 
| 
| 
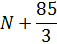
| 1,2 | 1,50 | 3,0 | 8,0 | 5,0 | 12,0 | 0,60 |
Выполнить следующие задания:
1. Найти радиусы всех окружностей на рисунке в метрах. Зададимся числом N=3. Радиус k-той зоны Френеля определяются формулой:
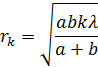
Круг радиуса R1 закрывает 23/6 зоны. Следовательно, для его вычисления следует положить k=23/6. Аналогично определятся радиусы других кругов.
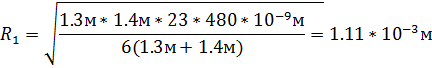
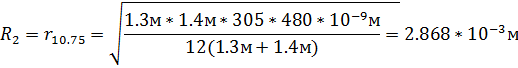
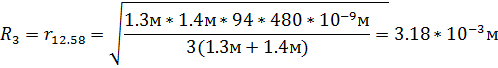
Пункт 1 выполнен.
2. Построить векторы амплитуд светового вектора для точки P от отдельных участков волнового фронта, проходящего через препятствие, найти их модули и указать направление. Интенсивность света в точке Р можно определить, суммируя колебания светового вектора, которые доставляются туда вторичными волнами от не закрытих преградой элементов волнового фронта. Мы полагаем, что свет может проходить только через незачерненные сегменты преграды, показанной на рисунке 1.
Суммирование колебаний будем выполнять с помощью спирали Френеля, которая показана на рисунке и выражает суммирование векторов колебаний в случае отсутсвия преграды, т.е. от полностью открытого волнового фронта. В 
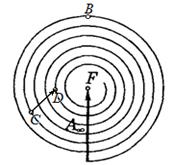этом случае амплитуда суммарного колебания выражается вектором, который на рисунке 3 обозначен как А∞. Если преграда открывает только небольшое количество зон Френеля, то от спирали Френеля остаются только внешние витки, которые можно считать окружностями единичного радиуса. При этом каждая точка спирали соответвтсвует воображаемой окружности на волновом фронте. Так начальная точка спирали (нижняя по рисунку 3) соот-ветствует центральной точке волновога фронта, лежащей на линии источник света – точка наблюдения. Диаметрально противоположная точка спирали (точка В на рисунке 3) соответствует воображаемой окружности на волновом фронте, ограничивающей первую зону Френеля. В общем случае можно мыс-ленно выделить кольцевой участок волнового фронта с ограничивающими его окружностями и найти на спирале Френеля точки, которые соответствуют этим ограничивющим окружностям. Направленный отрезок, соединяющий эти точки, будет суммарным вектором колебаний, которые доставляются в точку наблюдения от элементов выделенного кольцевого участка фронта. Для примера на рисунке показан вектор CD, который выражает колебание, приходящее в точку наблюдения от некого кольцевого участка светового фронта. При небольшом количестве открытых зон Френеля геометрические построения можно делать на единичной окружности, которая соответствует начальным виткам спирали Френеля.
Каждая из зон Френеля дает угловой вклад в спираль Френеля, равный π, следовательно, первый круг, покрывающий 23/6 зоны, даст вектор амплитуды светового вектора в виде хорды, стягивающей дугу величиной 23 π/6. Построение показано на рисунке 2. Модуль вектора можно найти как длину хорды, стягивающей дугу с углом α на окружности с радиусом r. Длина хорды выражается формулой: 
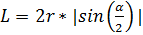. Используется абсолютная величина синуса, поскольку модуль должен быть положительным. В нашем случае L1=2*|sin(23π/12)|=0.524.
Круг с радиусом R2 покрывает 305/12=25.42 зон Френеля и соответствует на спирали Френеля углу, равному 25.42 π. Вектор амплитуды света – L2, даваемого кольцом с радиусами от R1 до R2 будет иметь начало в точке окончания вектора от первого круга с радиусом R1 и конец в точке окончания угла, соответствующего R2, т.е. 25.42 π, как показано на рисунке 3. Угол дуги, стягиваемой этим вектором, равен разности углов дуг, которые соответствуют радиусам R2 и R1, т.е. (305/12-23/6) π. Длина хорды, выражающей модуль вектора L2=2*|sin((25.42π-3.83π)/2)|=1.23.
Круг с радиусом R3 покрывает 94/3=31.3 зоны Френеля, что соответствует углу на спирали Френеля, равному 31.3π. Вектор амплитуды, даваемый третьим кольцом с радиусами от R2 до R3 будет иметь начало в точке окончания вектора амплитуды предыдущей части спирали и конец – в точке, соответствующе углу 31.3π. На рисунке 4 показан этот вектор – L3, который получается довольно маленьким. Длина хорды, выражающей модуль суммарного вектора L3=2*|sin((31.3π -25.42π)/2)|=0.27. На рис.4 обозначены также точки концов векторов L1, L2, L3, которые обозначены соответственно Т1, Т2, Т3
Пункт 2 выполнен
3. 
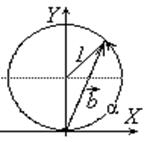
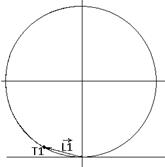
Построить и найти амплитуду светового вектора в точке P при наличии препятствия. Для построения суммарного вектора световых колебаний в точке Р введем систему координат, показанную на рисунке 5. Любой вектор b, составляющий угол α с осью Х и оканчивающийся на единичной окружности, будет иметь координатыты. xb=cos(α-π/2), yb=1+sin(α-π/2). Пользуясь этим правилом, вычислим координаты векторов L1, L2, L3 колебаний, определенных в предыдущем пункте решения. Вектор L1, показанный на рисунке 4, имеет координаты точки Т1:
xL1=cos(23π/6-0.5π)=-0.504; yL1=1+ sin(23π/6-0.5π)=0.136
Вычислим координаты вектора L2, который показан на рисунке 4. Они равны разностям координат конечной точки Т2 и начальной точки Т1. Координаты конечной точки вычислим по тому же правилу
xТ2=cos(25.42π-0.5 π)=-0.95; yТ2=1+sin(25.42π-0.5 π)=1.29
Теперь найдем координаты вектора L2:
xL2= xТ2- xL1=-0.45; yL2= yТ2- yL1=1.16
Аналогичные расчеты проведем для вектора L3, показанного на рисунке 6.
xТ3=cos(31.33π-0.5 π)=-0.84; yТ3=1+sin(31.33π-0.5 π)=1.542
xL3= xТ3- xТ2=0.11; yL3= yТ3- yТ2=0.252
Можно сделать проверку полученных результатов: модули векторов L1, L2, L3, вычисленные по их координатам, должны совпасть с модулями этих векторов, определенных в п 2.
Мы вычислили координаты трех векторов, характеризующие колебания, которые надо просуммировать для нахождения амплитуды результирующего светового вектора. Суммирование векторов необходимо сделать с учетом коэффициентов, обусловленных перекрытием некоторых частей волнового фронта препятствием.
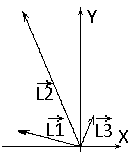Определим эти коэффициенты. Если часть кольцевой полосы фронта волны закрыта препятствием, то площадь закрытого участка не создает колебаний светового вектора в точке наблюдения. При этом длину вектора, изображающего колебание необходимо умножить на коэффициент, равный √(Sоткр/S), где Sоткр – площадь открытой части кольцевого сегмента, S – полная его площадь. Из рисунка препятствия в условии задачи легко опоределим отношения площадей и значения коэффициентов: k1= √(3/4), k2= √(3/4), k3=√(1/4). Умножение вектора на коэффициент сводится к умножению на этот коэффициент координат вектора. Обозначим умноженные на коэффициенты векторы через А. Тогда
xA1=xL1*k1=-0.442; yA1=yL1*k1=-0.442=0.1178
xA2=xL2*k2=-0.39; yA2=yL2*k2=1
xA3=xL3*k3=0.055; yA3=yL3*k3=0.126
На рис. 7 показаны векторы А, которые являются укороченными векторами L. В связи с этим рис.6 и рис.7 отличаются на сильно. Найдем координаты суммарного вектора В. Они являются суммами одноименных координат складываемых векторов:
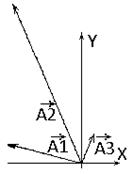хВ=хА1+хА2+хА3=-0.777; yВ=yА1+yА2+yА3=1.244
Определим модуль суммарного вектора, который соответствует амплитуде световых колебаний точке наблюдения.
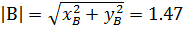Пункт 3 выполнен.
4. Найти отношение интенсивности света в точке наблюдения P при наличии препятствия к интенсивности I0 света в той же точке в отсутствие препятствия. Согласно правилам построения спирали Френеля, амплитуда светового вектора в точке наблюдения при отсутствии преград будет равна радиусу внешних витков спирали, т. Е. единице. Все построения и вычисления, которые сделаны нами удовлетворяли правилам спирали Френеля. Следовательно, модуль вектора амплитуды результирующего колебания в точке наблюдения даст относительную амплитуду колебаний в этой точке при заданной преграде. В нашем случае |A|=1.46. Интенсивность пропорциональна квадрату амплитуды. Поэтому интенсивность света в точке наблюдения равна:
I=I0*A2=2.15I0
Интенсивность света при наличии заданной преграды оказалась более чем вдвое больше в сравнении со случаем отсутствия преград. Это проявление фокусирующих свойств набольших отверстий. Известно, что зонная пластинка многократно увеличивает интенсивность света в точке своего фокуса. Пункт 4 выполнен.
На дифракционную решетку, содержащую n1 штрихов на 1мм длины, падает нормально свет с длиной волны λ. Расстояние от решетки до экрана L. Найти общее число наблюдаемых максимумов и расстояние от центрального максимума до последнего наблюдаемого. Пусть на решетку падает белый свет с длинами волн в интервале (450÷700) нм. Найти длину спектра второго порядка. Начиная со спектров каких порядков наблюдается их перекрытие?
Положение главных максимумов при дифракции на решетке определяется формулой d*sin(φ)=kλ, в которой d-период решетки, k – целое число – порядок главного максимума. Полагая φ=π/2, определим максимально возможный порядок
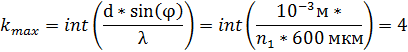
(Функция int(х) – взятие от дроби только целой части.)
Общее число видимых на экране главных максимумов, включая центральный будет равно 9. Четыре по обе стороны от центрального - нулевого.
Найдем угол направления на последний главный максимум
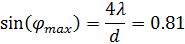
Следовательно, φmax=0.95 рад. (46.6о)
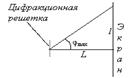
Расстояние от центрального до четвертого максимума определится из чертежа, показанного на рисунке 13
l=L*tg(φmax)=1.82 м
Предположим, что решетка освещается белым светом, λmin=450 нм,, λmax=700 нм. Тогда максимум второго порядка для фиолетовых лучей будет под углом φ1, который определится уравнением:
Максимум второго порядка для красных лучей удовлетворяет такому же уравнению:
Из этих уравнений найдем
sin(φф)=2* λmin/d=0.306 => φф=0.37 рад
sin(φкр)=2* λmax/d=0.47 => φкр=0.49 рад
Теперь определим расстояние на экране между максимумами для красных и фиолетовых лучей, это будет протяженностью спектра второго порядка
Δl=L(tg(φкр) – tg(φф))=0.189 м.
Дифракционная решетка отклоняет красные лучи сильнее, чем фиолетовые. Поэтому красная часть спектра k-того порядка может наложиться на фиолетовую часть k+1 порядка. В качестве условия такого наложения возьмем равенство синусов углов отклонения:
sin(φф)=(k+1)* λmin/d = sin(φкр)=k* λmax/d
Из этого равенства получим
(k+1)* λmin = k* λmax => 1+1/k=1.5555 => k=1.8
Это означает, что красная часть спектра второго порядка наложится на фиолетовую часть спектра третьего порядка.
Пункт 8 выполнен.
Проектируем электролампочку с вольфрамовой нитью накала. Заданными величинами являются: мощность – Р, поглощающая способность вольфрама – k, напряжение питания – U, абсолютная температура горячей нити – T.
| Вариант | Р Вт | k | U B | T K |
| 0.5 | ||||
| 0.4 | ||||
| 0.55 | ||||
| 0.6 | ||||
| 0.65 | ||||
| 0.7 | 12.6 | |||
| 0.4 | ||||
| 0.5 | 6.3 | |||
| 0.55 | 12.6 | |||
| 0.7 |
Требуется вычислить диаметр и длину нити.
Удельное сопротивление вольфрама при температуре t=20оС принять равным 5.5*10-8 Ом*м, температурный коэффициент удельного сопротивления вольфрама α=4.8*10-3 1/К.
Определить длину волны, на которую приходится максимум излучения лампочки.
Решение. Возьмем следующие исходные данные=200 Вт, k=0.5, U=220 B, T=2400 K.
Излучаемая мощность равна поглощаемой электрической мощности. По закону Стефана – Больцмана запишем::
Где S – площадь боковой поверхности нити накала. Если l – длина нити, d – ее диаметр, то
И после подстановки площади получим:
Электрическое сопротивление нити накала выражается через длину нити и площадь ее поперечного сечения, которая равна πd2/4:
Где ρ – удельное сопротивление вольфрама, которое зависит от температуры. Данная зависимость является линейной и выражается следующей формулой:
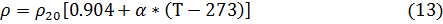
Громоздкость этой формулы обусловлена тем, что в справочниках приводится удельное сопротивление металлов при температуре 20оС, в то время как нам необходима зависимость удельного сопротивления от абсолютной температуры (в Кельвинах). Можно немного преобразовать формулу, используя известное значение температурного коэффициента для вольфрама: α=4.8*10-3 1/К:
С учетом этой формулы сопротивление нити накала выразится следующей формулой:
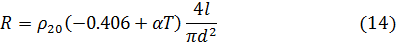
С другой стороны, сопротивление нити накала выражается через электрическую мощность:
Из двух последних равенств будем иметь следующее уравнение:
Из которого выразится длина нити:
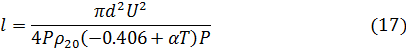
После подстановки (33) в (27) получим уравнение для диаметра нити:
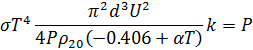
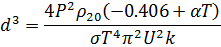
Поскольку формула получена путем множества преобразований и подстановок, необходима проверка размерности:
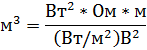
Размерность левой и правой части равенства совпадают, это позволяет надеется на правильность результата. Подставим числовые данные:
Подставим полученное значение диаметра в формулу для длины нити (17):
Задачи для решения на практических занятиях (они включаются в экзаменационные билеты)
:
Геометрическая оптика
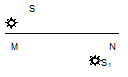
1. На рисунке S – точечный источник света, S1 – его изображение. Определить построением оптический центр линзы и ее фокусы, если главной оптической осью линзы является прямая MN.
2. Собирающая линза даёт в три раза увеличенное действительное изображение предмета. Чтобы получить в три раза увеличенное, но мнимое изображение, линзу передвинули в сторону предмета на а = 10 см. Каково фокусное расстояние линзы?
3. Система состоит из положительной линзы, с силой 10 дптр, и отрицательной линзы, с силой -3 дптр. Расстояние между линзами 5 см. Определить положение изображения и увеличение, если предмет находится на оптической оси на расстоянии 15 см от положительной линзы.
4. 
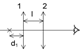Оптическая система из двух собирающих линз на расстоянии l=0,75 м друг от друга превращает свет источника, находящегося на расстоянии 25 см от первой линзы в параллельный пучок. Найти оптическую силу второй линзы, если у первой она равна 6 дптр.
Фотометрия
5. 
Светильник в виде шара радиусом R=10 см имеет силу света J=100 кд. Определить полный световой поток - Ф, светимость поверхности – М.
6. На какую высоту над верстаком необходимо повесить светильник с лампочкой мощностью 300 Вт, чтобы освещенность стола под светильником составляла 100 лкс. Наклон стола составляет 30о с горизонталью, а световая отдача светильника равна 20 лм/Вт.
7. На высоте 2м над серединой круглого стола диаметром 3 м висит лампа силой света 100 кд. Ее заменили лампой с силой света 25 кд, изменив расстояние до стола так, что освещенность середины стола не изменилась. Во сколько раз изменится освещенность края стола
Интерференция
8. В опыте Юнга расстояние между щелями 1 мм, расстояние от щелей до экрана 1 м, используется красный свет (λ=720 нм). Определить ширину интерференционных полос.
9. Бипризма Френеля имеет угол α=2о и сделана из стекла с n=1.5. Освещенная щель – источник света расположена на расстоянии 10 см от призмы, а экран – по другую сторону на расстоянии 60 см. Ширина полученных интерференционных полос равна 0.43 мм. Определить длину волны используемого света.
10. Вычислить толщину просветляющей пленки и требуемый показатель преломления ее материала, если ее необходимо нанести на поверхность линзы, сделанной из стекла с показателем преломления n=1.5.
11. На мыльную пленку с показателем прело мления n = 1,33 падает по нормали монохроматический свет с длиной волны λ=0,6 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая возможная толщина d пленки?
Дифракция
12. Сколько зон Френеля уместится в отверстии диаметром 0.5 мм, если расстояние от источника света до отверстия равно 10 см, а от отверстия до экрана – 10 мм. Длина волны света равна 550 нм.
13. Фазовая зонная пластинка изготавливается из стекла с коэффициентом преломления 1.5. Определить радиусы колец, на которых необходимо утолщение пластинки и величину утолщения, если пластинка должна заменить линзу с оптической силой 15 дптр. Длина волны света λ=0.55 мкм.
14. На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки d=2 мкм. Определить наибольший порядок дифракционного максимума, который дает эта решетка в случае красного (λ=0,7 мкм) и в случае фиолетового (λ=0,41 мкм) света.
15. На грань кристалла падает параллельный пучок рентгеновских лучей с длиной волны 0.075 нм. Расстояние между атомными плоскостями равно 0.2 нм. Под каким углом скольжения следует направить лучи на поверхность, чтобы получить дифракционный максимум 1 порядка.
Поляризация света
16. Из воздуха на плоскую поверхность стекла перпендикулярно падает свет с интенсивностью I0. Показатель преломления стекла n=1.5. Определить интенсивность отраженной и прошедшей в стекло волн.
17. Из воздуха на плоскую поверхность стекла под углом Брюстера падает свет с интенсивностью I0. Показатель преломления стекла равен 1.6. Определить величину угла падения и интенсивность отраженного света.
Тепловое излучение
18. Абсолютно черный радиатор должен рассеять мощность 15 Вт. Температура окружающей среды 27оС, допустимая температура радиатора 60оС. Пренебрегая другими видами теплоотдачи кроме излучения, определить необходимую площадь радиатора.
19. Электрическая лампа имеет площадь излучающей поверхности, равную 2.16 см2. Температура нити накала – 2365 К, излучение нити составляет 0.7 излучения абсолютно черного тела при данной температуре. Найти мощность лампочки.
Квантовая физика
20. Красная граница фотоэффекта λ0=0.545 мкм, максимальная кинетическая энергия фотоэлектрона Wmax=0.5 эв, определить долю энергии фотона, израсходованной на работу вырывания фотоэлектрона.
21. Определить релятивистский импульс электрона, обладающего кинетической энергией Т=2 Мэв.
22. Скорость электрона v = 0,75С (гдe С скорость света в вакууме). зная энергию покоя электрона Е0=0.51 Мэв, определить в тех же единицах кинетическую энергию Т электрона
23. Микрочастица находится в бесконечно глубокой потенциальной яме на первом энергетическом уровне (n=1). Определить вероятность обнаружения частицы в средней трети ямы.
24. Протон находится в бесконечно глубокой одномерной потенциальной яме шириной l0-10 м. Рассчитать расстояние между 2 и 3 энергетическими уровнями. (масса протона 1.67*10-27 кг кг).
Атомная физика
25. С помощью энергетической диаграммы Хунда записать электронное строение атома cl
26. Рассчитать длины волн в спектре излучения атома водорода, соответствующих переходам серии Бальмера. Постоянную Ридберга для 1/λ Rν=1.097*107 м-1.
Ядерная физика
27. При соударении α-частицы с ядром бора 
произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода 
. Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции. (применить законы сохранения заряда и числа нуклонов).
28. Определить число N атомов радиоактивного препарата йода 
массой 0,5 мкг, распавшихся в течение 1 минуты. (Период полураспада йода – 8 суток).
29. Определить активность через неделюрадиоактивного препарата 86Rn122, период полураспада которого Т=3.8 суток. Масса препарата m= 0.15 мкг.
30. Определить возраст археологических находок из древесины, если активность образцов по изотопу 6С14 составляет 0.6 активности образцов из свежих растений. Период полураспада изотопа 6С14 равен 5730 лет
